Добавлен: 08.11.2023
Просмотров: 219
Скачиваний: 13
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
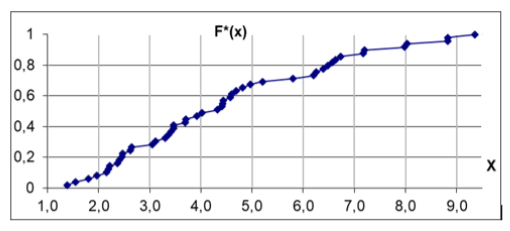
Задача 10. Обработка одномерной выборкиУсловие задачиПо выборке одномерной случайной величины:- получить вариационный ряд;- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);- построить гистограмму равно интервальным способом;- построить гистограмму равновероятностным способом;- вычислить точечные оценки математического ожидания и дисперсии;- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия 2 и критерия Колмогорова (= 0,05). График гипотетической функции распределения F0(x) построить совместно с графиком F*(x) в той же системе координат и на том же листе.Решение.
Эмпирическая функция распределения случайной величины X равна частоте того, чтоX примет значение меньшее, чем аргумент функции x, и определяется формулойКоличество интервалов M, необходимое для построения гистограмм, определим по объему выборки:Шаг интервалаh=h= (9,35-1,39)/7=1,137гистограмма, построенная равно интервальным способомгистограмма построенная равновероятностным способом;Вычислим точечную оценку математического ожидания по формуле:Вычислим точечную оценку дисперсии по формуле: .Построим доверительный интервал для математического ожидания с надежностью γ = 0,95. Для этого в таблице функции Лапласа найдем значение, равное = 0,475, и определим значение аргумента, ему соответствующее: . Затем вычислим и получим доверительный интервал для математического ожидания: .Построим доверительный интервал для дисперсии с надежностью γ = 0,95 по формуле. Вычислим и получим доверительный интервал для дисперсии:
.По виду гистограммы выдвинем гипотезу о равномерном распределении СВХ. Проверим гипотезу о равномерном распределении СВХ при помощи критерия χ2Н0: F(x)=F0(x)Н1: F(x)≠F0(x)Где ,F0(x)– теоретическая плотность и функция распределенияГде χ2= =0,143ni’=49*0,143=7
χ2=49*0.2041=10,0По таблице найдем критическое значение критерия χ2кр (5;0,05) =11,1, так как χ2кр> χ2 то гипотеза о равномерном распределении СВ Х принимается.Проверим гипотезу о равномерном распределении СВ Х при помощи критерия КолмогороваН0: F(x)=F0(x)Н1: F(x)≠F0(x)Где F0(x)– теоретическая функция распределенияПо графику определим максимальное по модулю отклонение между функциями и :Вычислим значение критерия Колмогорова по формуле:
Из таблицы Колмогорова по заданному уровню значимости =0,05 выбираем критическое значение Так как , то гипотезу о равномерном законе распределения не принимаем.Задача 11. Обработка двухмерной выборкиУсловие задачиПо выборке двухмерной случайной величины:- вычислить точечную оценку коэффициента корреляции;- вычислить интервальную оценку коэффициента корреляции (γ = 0,95);- проверить гипотезу об отсутствии корреляционной зависимости;- вычислить оценки параметров a0 и a1 линии регрессии ;- построить диаграмму рассеивания и линию регрессии.Решение.Состоятельная оценка коэффициента корреляцииРасчетная таблица
=-4,9136 =3,9636 =-30,3057 =35,5957 =26,2695 =3,317 =3,454дисперсия 11,929 =10,999Состоятельная оценка коэффициента корреляции =-0,985Уравнение регрессии имеет видY-3,9636=-0,985*(3,317/3,454)(x+4,9136)y=-0,946x-0,683a0=-0,946a1=-0,683проверим значимость коэффициента корреляции, при помощи критерия tH0: =0H1: 0t=t= =-27,24по таблице найдем критическое значение Tкр(0,05;23)=2,09, так как |t|>Tкр то коэффициент корреляции значим.Доверительный интервал для коэффициента корреляцииГде Для -2,8556 -2,0198
| 1,39 |
| 1,55 |
| 1,8 |
| 1,97 |
| 2,15 |
| 2,19 |
| 2,22 |
| 2,37 |
| 2,41 |
| 2,45 |
| 2,47 |
| 2,62 |
| 2,64 |
| 3,05 |
| 3,11 |
| 3,3 |
| 3,36 |
| 3,42 |
| 3,46 |
| 3,47 |
| 3,69 |
| 3,71 |
| 3,92 |
| 4,02 |
| 4,32 |
| 4,41 |
| 4,43 |
| 4,44 |
| 4,58 |
| 4,6 |
| 4,69 |
| 4,82 |
| 4,96 |
| 5,21 |
| 5,8 |
| 6,2 |
| 6,25 |
| 6,39 |
| 6,48 |
| 6,57 |
| 6,63 |
| 6,73 |
| 7,17 |
| 7,2 |
| 7,98 |
| 8,03 |
| 8,82 |
| 8,82 |
| 9,35 |
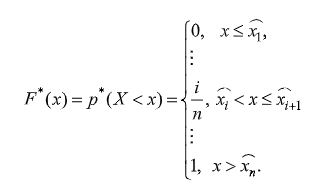
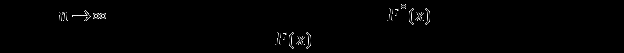
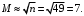
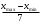
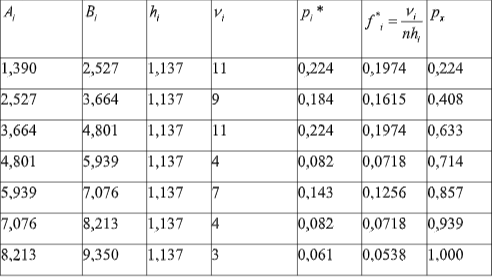
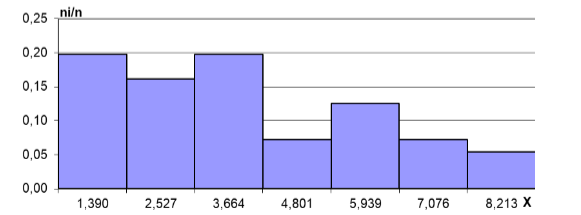
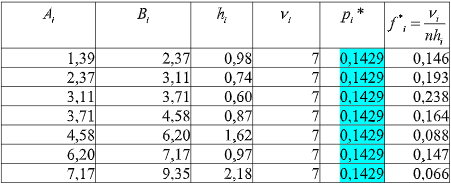
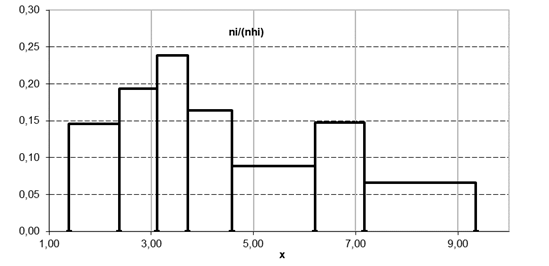
Эмпирическая функция распределения случайной величины X равна частоте того, чтоX примет значение меньшее, чем аргумент функции x, и определяется формулойКоличество интервалов M, необходимое для построения гистограмм, определим по объему выборки:Шаг интервалаh=h= (9,35-1,39)/7=1,137гистограмма, построенная равно интервальным способомгистограмма построенная равновероятностным способом;Вычислим точечную оценку математического ожидания по формуле: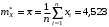Вычислим точечную оценку дисперсии по формуле: 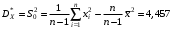.Построим доверительный интервал для математического ожидания с надежностью γ = 0,95. Для этого в таблице функции Лапласа найдем значение, равное 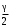= 0,475, и определим значение аргумента, ему соответствующее: 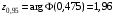. Затем вычислим 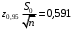и получим доверительный интервал для математического ожидания: 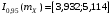.Построим доверительный интервал для дисперсии с надежностью γ = 0,95 по формуле. Вычислим 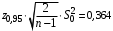и получим доверительный интервал для дисперсии:
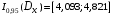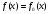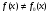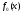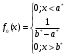
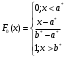
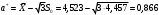
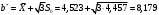
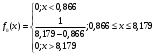
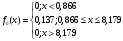
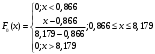
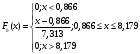
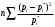
.По виду гистограммы выдвинем гипотезу о равномерном распределении СВХ. Проверим гипотезу о равномерном распределении СВХ при помощи критерия χ2Н0: F(x)=F0(x)Н1: F(x)≠F0(x)Где ,F0(x)– теоретическая плотность и функция распределенияГде χ2= 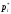=0,143ni’=49*0,143=7
 |  |  |  |  |  |
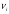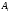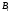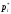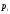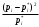| 11 | 1,390 | 2,527 | 0,1429 | 0,2245 | 0,0466 |
| 9 | 2,527 | 3,664 | 0,1429 | 0,1837 | 0,0117 |
| 11 | 3,664 | 4,801 | 0,1429 | 0,2245 | 0,0466 |
| 4 | 4,801 | 5,939 | 0,1429 | 0,0816 | 0,0262 |
| 7 | 5,939 | 7,076 | 0,1429 | 0,1429 | 0,0000 |
| 4 | 7,076 | 8,213 | 0,1429 | 0,0816 | 0,0262 |
| 3 | 8,213 | 9,350 | 0,1429 | 0,0612 | 0,0466 |
| | | сумма | 1,0000 | 1,0000 | 0,2041 |
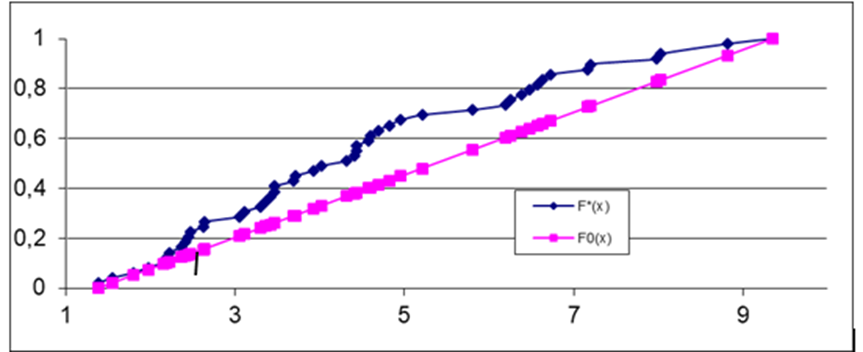
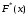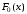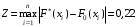
χ2=49*0.2041=10,0По таблице найдем критическое значение критерия χ2кр (5;0,05) =11,1, так как χ2кр> χ2 то гипотеза о равномерном распределении СВ Х принимается.Проверим гипотезу о равномерном распределении СВ Х при помощи критерия КолмогороваН0: F(x)=F0(x)Н1: F(x)≠F0(x)Где F0(x)– теоретическая функция распределенияПо графику определим максимальное по модулю отклонение между функциями и :Вычислим значение критерия Колмогорова по формуле:
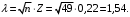
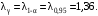
Из таблицы Колмогорова по заданному уровню значимости =0,05 выбираем критическое значение Так как 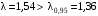, то гипотезу 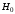о равномерном законе распределения не принимаем.Задача 11. 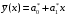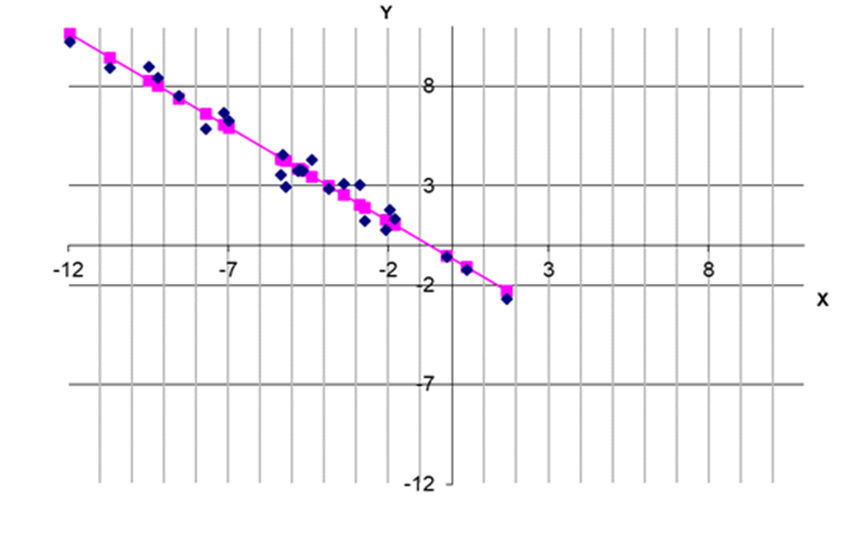Обработка двухмерной выборкиУсловие задачиПо выборке двухмерной случайной величины:- вычислить точечную оценку коэффициента корреляции;- вычислить интервальную оценку коэффициента корреляции (γ = 0,95);- проверить гипотезу об отсутствии корреляционной зависимости;- вычислить оценки параметров a0 и a1 линии регрессии ;- построить диаграмму рассеивания и линию регрессии.Решение.Состоятельная оценка коэффициента корреляции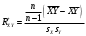Расчетная таблица| | X | Y | X*Y | X2 | Y2 |
| | -11,95 | 10,25 | -122,4875 | 142,8025 | 105,0625 |
| | -6,99 | 6,28 | -43,8972 | 48,8601 | 39,4384 |
| | -5,34 | 3,56 | -19,0104 | 28,5156 | 12,6736 |
| | -4,37 | 4,32 | -18,8784 | 19,0969 | 18,6624 |
| | -5,29 | 4,57 | -24,1753 | 27,9841 | 20,8849 |
| | -8,53 | 7,53 | -64,2309 | 72,7609 | 56,7009 |
| | -10,68 | 8,91 | -95,1588 | 114,0624 | 79,3881 |
| | -7,14 | 6,66 | -47,5524 | 50,9796 | 44,3556 |
| | -9,2 | 8,44 | -77,6480 | 84,6400 | 71,2336 |
| | -7,69 | 5,83 | -44,8327 | 59,1361 | 33,9889 |
| | -0,18 | -0,6 | 0,108 | 0,0324 | 0,36 |
| | -2,88 | 3,02 | -8,6976 | 8,2944 | 9,1204 |
| | -4,76 | 3,8 | -18,088 | 22,6576 | 14,44 |
| | -9,47 | 8,95 | -84,7565 | 89,6809 | 80,1025 |
| | -3,39 | 3,09 | -10,4751 | 11,4921 | 9,5481 |
| | -1,96 | 1,77 | -3,4692 | 3,8416 | 3,1329 |
| | -1,8 | 1,34 | -2,412 | 3,24 | 1,7956 |
| | -4,81 | 3,75 | -18,0375 | 23,1361 | 14,0625 |
| | -5,2 | 2,92 | -15,184 | 27,04 | 8,5264 |
| | 0,45 | -1,26 | -0,567 | 0,2025 | 1,5876 |
| | -2,73 | 1,24 | -3,3852 | 7,4529 | 1,5376 |
| | -4,68 | 3,76 | -17,5968 | 21,9024 | 14,1376 |
| | -3,86 | 2,85 | -11,001 | 14,8996 | 8,1225 |
| | 1,69 | -2,69 | -4,5461 | 2,8561 | 7,2361 |
| | -2,08 | 0,8 | -1,664 | 4,3264 | 0,64 |
| сумма | -122,84 | 99,09 | -757,6436 | 889,8932 | 656,7387 |
| среднее | -4,9136 | 3,9636 | -30,3057 | 35,5957 | 26,2695 |
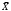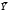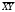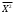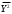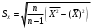
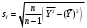
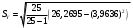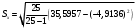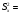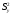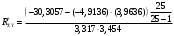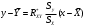
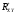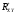
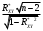
=-4,9136 =3,9636 =-30,3057 =35,5957 =26,2695 =3,317 =3,454дисперсия 11,929 =10,999Состоятельная оценка коэффициента корреляции =-0,985Уравнение регрессии имеет видY-3,9636=-0,985*(3,317/3,454)(x+4,9136)y=-0,946x-0,683a0=-0,946a1=-0,683проверим значимость коэффициента корреляции, при помощи критерия tH0: =0H1: 0t=t= 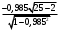=-27,24по таблице найдем критическое значение Tкр(0,05;23)=2,09, так как |t|>Tкр то коэффициент корреляции значим.Доверительный интервал для коэффициента корреляции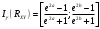Где 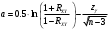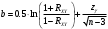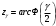Для 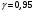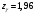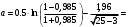-2,8556 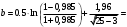-2,0198