Файл: Решение балансовых уравнений с помощью обратной матрицы.rtf
Добавлен: 08.11.2023
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Негосударственное образовательное учреждение
Высшего профессионального образования
"Сибирский институт бизнеса и информационных технологий"
РЕФЕРАТ
Дисциплина: Математика
Тема: Решение балансовых уравнений с помощью обратной матрицы
Выполнил: студент группы УПНоз-1222(2)
Жмакина Анастасия Сергеевна
Омск 202
Содержание
Введение 2
1. Матрицы 3
1.1 Понятие матрицы 3
1.2 Понятие обратной матрицы 5
2. Системы линейных уравнений 6
2.1 Основные понятия и определения 6
2.2 Методы решения систем линейных алгебраических уравнений 8
2.2.1 Метод обратной матрицы 8
3. Модель Леонтьева многоотраслевой экономики 8
3.1 Балансовый анализ. Основная задача межотраслевого баланса 8
3.2 Составление и решение балансового уравнения с помощью обратной матрицы 12
Заключение 17
Библиографический список 18
Введение
Математика интенсивно проникает в другие науки: во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Язык математики универсален, что является объективным отражением универсальности законов окружающего нас мира.
Экономика как наука об объективных причинах функционирования и развития общества пользуется разнообразными количественными характеристиками, а потому вобрала в себя большое число математических методов. Современная экономика использует методы, разработанные в XX в. Л.В. Канторовичем, В.В. Леонтьевым, Е.Е. Слуцким. В это же время интенсивно развивался и математический аппарат, применяемый в экономике.
Использование элементов алгебры матриц является одним из основных методов решения многих экономических задач. Этот вопрос стал особенно актуальным при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.
Также существует ряд экономических задач, приводящих к составлению и решению систем линейных алгебраических уравнений на основе прогноза выпуска продукции по известным запасам сырья.
На основе алгебры матриц и аппарате матричного анализа американский экономист В.В. Леонтьев создал математическую модель, которая решает проблему баланса между отдельными отраслями мирового хозяйства.
Таким образом, применение элементов линейной алгебры в значительной степени упрощает способы решения многих задач экономики.
Тема моей работы: "Решение балансовых уравнений с помощью обратной матрицы".
Цель: обобщение и систематизация теоретического материала в рамках исследуемой проблемы.
Задачи.
-
Проанализировать литературу по математике и экономике. -
Подобрать необходимый теоретический и практический материал из раздела линейной алгебры и адаптировать его. -
Подобрать серию экономических задач и показать их решение с помощью элементов линейной алгебры.
1. Матрицы
1.1 Понятие матрицы
Понятие матрицы и основанный на нем раздел математики - матричная алгебра - имеют чрезвычайно важное значение для экономистов.
Определение 1. Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными заглавными буквами латинского алфавита, например, А, В, С,…, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: aij, где i - номер строки, j - номер столбца.
Например, матрица А =
или в сокращенной записи А =
, где i = 1, 2, …, m; j = 1,2, …, n.Определение 2. Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, то есть аij =bij для любых i =1,2, …,m; j=1,2, …,n.
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики:
| Ресурсы | Отрасли экономики | |
| промышленность | сельское хозяйство | |
| Электроэнергия | 5,3 | 4,1 |
| Трудовые ресурсы | 2,8 | 2,1 |
| Водные ресурсы | 4,8 | 5,1 |
Данная таблица может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
5,3 4,1
А= 2,8 2,1
4,8 5,1.
В этой записи, например, элемент а11=5,3 показывает, сколько электроэнергии потребляет промышленность, а элемент а22 =2,1 - сколько трудовых ресурсов потребляет сельское хозяйство.
Использование элементов алгебры матриц является одним из основных методов решения многих экономических задач. Этот вопрос стал особенно актуальным при разработке и использовании баз данных: при работе с ними почти вся информация хранится и обрабатывается в матричной форме.
1.2 Понятие обратной матрицы
Понятие обратной матрицы распространяется только на квадратные матрицы.
Определение 3. Матрица порядка n называется вырожденной, если ее ранг r < п.
Определение 4. Матрица A-1 называется обратной по отношению к матрице A, если их произведение равно единичной матрице:
A·A-1 = A-1·A = E.
обратная матрица балансовое уравнение
Для вырожденной матрицы не существует обратной матрицы. Иными словами, если для некоторой матрицы порядка n ее ранг г < n, то для нее не существует обратной матрицы.
2. Системы линейных уравнений
2.1 Основные понятия и определения
Система m линейных уравнений с n переменными имеет вид:
а
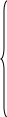11х1 + а12х2 + … + а1nхn = b1а21х1 + а22х2 + … + а2nхn = b2
… (1)
аi1х1 + аi2х2 + … + аinхn = bi
…
аm1х1 + аm2х2 + … + аmnхn = bm
где аij, bi (i = 1,2, …, m; j = 1,2, …,n) - произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
В более краткой записи с помощью знаков суммирования систему можно записать в виде:
n
Σ aijxj = bi (i = 1, 2, …, m).
j=1
Определение 5. Решением данной системы называется такая совокупность n чисел (х1 = к1, х2 = к2, …, хn = кn), при подстановке которых каждое уравнение системы обращается в верное равенство.
Определение 6. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Определение 7. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Определение 8. Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
С помощью элементарных преобразований системы уравнений, рассмотренных применительно к матрицам (например, умножение обеих частей уравнений на числа, не равные нулю; сложение уравнений системы), получается система, равносильная данной.
Запишем систему (1) в матричной форме. Обозначим:
а11 а12 … а1n х1b1
А = а21 а22 … а2n; Х = х2; В = b2,… … … … ……
аm1 аm2 … аmn хn bm
где А - матрица коэффициентов при переменных, или матрица системы, Х - матрица-столбец переменных, В - матрица-столбец свободных членов.
Так как число столбцов матрицы Аm×n равно числу строк матрицы Хn×1, то их произведение
а11х1 + а12х2 + … + а1nхnАХ = а21х1 + а22х2 + … + а2nхn есть матрица-столбец.
…
аm1х1 + аm2х2 + … + аmnхn
Элементами полученной матрицы являются левые части системы (1). На основании определения равенства матриц систему (1) можно записать в виде:
АХ = В.
2.2 Методы решения систем линейных алгебраических уравнений
2.2.1 Метод обратной матрицы
Рассмотрим случай, когда число уравнений равно числу неизвестных, т.е. т = п. Система уравнении имеет вид:
а
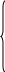11х1 + а12х2 + … + а1nхn = b1а21х1 + а22х2 + … + а2nхn = b2 (A)
…
аn1х1 + аn2х2 + … + аnnхn = bn
В матричной форме система уравнений имеет вид АХ = В.
Пусть матрица системы А является невырожденной, т.е. существует обратная матрица А-1. Умножив обе части этого уравнения слева на А-1, получаем решение данной системы в матричной форме:
X = А-1B.
3. Модель Леонтьева многоотраслевой экономики
3.1 Балансовый анализ. Основная задача межотраслевого баланса
Цель балансового анализа - ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом, каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой - как потребитель продукции и своей, и произведенной другими отраслями.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 году американским экономистом В. Леонтьевым.
Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени, например, за год.
Введем следующие обозначения:
xi - общий (валовой) объем продукции i - ой отрасли (i = 1, 2, …,n);
хij - объем продукции i - ой отрасли, потребляемой j - ой отраслью в процессе производства (i,j = 1, 2, …,n);
yi - объем конечного продукта i - ой отрасли для непроизводственного потребления.
Так как валовой объем продукции любой i - ой отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то
n
xi = Σ xij + yi, (i = 1, 2, …,n). (1)
j = 1
Уравнения (1) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в уравнения (1), имеют стоимостное выражение.
Введем коэффициенты прямых затрат
хij
аij = хj, (i,j = 1, 2, …,n), (2)показывающие затраты продукции i - ой отрасли на производство единицы продукции j - ой отрасли.
Можно полагать, что в некотором промежутке времени коэффициенты аij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, то есть
xij = аij хj, (i,j = 1, 2, …,n), (3)
вследствие чего, построенная на этом основании модель межотраслевого баланса получила название линейной.
Теперь соотношения баланса (1) примут вид:
n
xi = Σ аij хj + yi, (i = 1, 2, …,n). (4)
j = 1
х1 а11 а12 … а1n у1Обозначим Х = х2, А = а21 а22 … а2n, Y = у2, (4')
……………………. …
хn аn1 аn2 … аnn уn
где Х - матрица-столбец валового выпуска, Y - матрица-столбец конечного продукта, А - матрица прямых затрат (технологическая или структурная матрица). Тогда систему (1) можно записать в матричном виде:
Х = АХ + Y. (5)
Основная задача межотраслевого баланса состоит в отыскании такой матрицы валового выпуска Х, которая при известной матрице прямых затрат А обеспечивает заданную матрицу конечного продукта Y.
Перепишем уравнение (5) в виде:
Х - АХ = Y или ЕХ - АХ = Y,
отсюда по свойству дистрибутивности умножения матриц относительно сложения имеем:
(Е - А) Х = Y. (6)
Если матрица (Е - А) невырожденная, то есть | E - A | ≠0, то получаем
Х = (Е - А) - 1Y. (7)
Матрица S = (Е - А) - 1 называется матрицей полных затрат.
Чтобы выяснить экономический смысл элементов матрицы S = (sij), зададим единичными матрицами конечного продукта Y'1 = (1,0, …, 0), Y'2 = (0,1,…, 0), …, Y'n = (0,0, …,1), где знак "'" означает транспонирование матриц. Тогда по уравнению (7) соответствующие матрицы валового выпуска имеют вид: Х'1 = (s11, s21, …, sn1), X'2 = (s12, s22, …, sn2), …, X'n = (s1n, s2n, …, snn).
Следовательно, каждый элемент sij матрицы S есть величина валового выпуска продукции i - ой отрасли, необходимого для обеспечения выпуска единицы конечного продукта j - ой отрасли yj = 1 (j = 1, 2, …, n).
В соответствии с экономическим смыслом задачи значения xi должны быть неотрицательны при неотрицательных значениях yi ≥ 0 и aij ≥ 0, где i,j = 1, 2, …,n.
Матрица А ≥ 0 называется продуктивной, если для любой матрицы Y ≥ 0 существует решение Х ≥ 0 уравнения (6). В этом случае и модель Леонтьева называется продуктивной.
Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы:
причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.3.2 Составление и решение балансового уравнения с помощью обратной матрицы
Балансовое уравнение появляется в линейной модели экономики (модели Леонтьева) и может применяться для анализа и планирования деятельности предприятия, отрасли, а также экономики страны в целом. Рассмотрим суть этой модели на простейшем примере.
Предприятие производит три вида продукции в количестве х1, х2 и х3 единиц каждого вида. Часть этой продукции расходуется внутри производства, а оставшаяся часть (товарная продукция) реализуется за пределами производства, поэтому можно, исходя из условия, что продукция каждого вида должна обеспечивать внутрипроизводственное потребление и запланированный объем продаж, составить систему уравнений:
х1 = х11 + х12 + х13 + y1, х1 - х11 - х12 - х13 = y1,х2 = х21 + х22 + х23 + y2, или х2 - х21 - х22 - х23 = y2,х3 = х31 + х32 + х33 + y3, х3 - х31 - х32 - х33 = y3.
Здесь хij - количество продукции вида i, расходуемое на производство продукции вида j, например х23 - количество продукции второго вида, расходуемое на производство продукции третьего вида. Если разделить это количество на х3, то можно найти, сколько продукции второго вида расходуется при производстве единицы продукции третьего вида.
Аналогично, отношение
показывает, какое количество продукции вида i расходуется при производстве единицы продукции вида j. Поскольку такой расход зависит от используемой в производстве технологии, то указанное отношение называется технологическим коэффициентом. Обозначим егоaij =
и, учитывая, что хij = aij хj, перепишем вторую систему в виде:х1 - a11х1 - a12х2 - a13х3 = y1,х2 - a21х1 - a22х2 - a23х3 = y2,х3 - a31х1 - a32х2 - a33х3 = y3.
Введем в рассмотрение три матрицы: матрицу А, составленную из техно - логических коэффициентов (технологическую матрицу или матрицу Леонтьева), матрицу X, характеризующую выпуск продукции (производственный вектор) и матрицу Y (вектор товарной продукции или конечного спроса).
а11 а12 а13 x1 y1
А = а21 а22 а23 Х = х2 Y = y2,а 31 а32 а33 х3 y3
Используя введенные обозначения и помня правила действий с матрицами, систему можно записать в матричном виде:
X - AX = Y или (E - A) X = Y.
Составленное матричное уравнение и называется балансовым уравнением, его решение можно найти с помощью обратной матрицы:
X = (E - A) - 1Y.
Применить его можно следующим способом. По результатам деятельности предприятия за истекший период составляют балансовое уравнение и находят матрицу B = (E - A) - 1, которая называется матрицей полных производственных затрат. Элемент этой матрицы bij равен величине продукции i - того вида, необходимой для производства единицы товарной продукции j - того вида. Затем, зная величину конечного спроса на продукцию YH на новый производственный период, определим новый производственный вектор XH по формуле
XH = (E - A) - 1 YH =BYH.
Матрицу B можно найти по формуле обратной матрицы через алгебраические дополнения, а можно по приближенной формуле:
B ≈ E + A + A2 + A3.
Рассмотрим пример решения задачи с использованием модели Леонтьева.
Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Валовая продукция | Из нее использовано для производства продукции подразделениями | Конечная (товарная) продукция | ||
| 1 | 2 | 3 | |||
| 1 | 100 | 10 | 5 | 40 | 45 |
| 2 | 100 | 30 | - | 30 | 40 |
| 3 | 200 | 20 | 20 | - | 140 |
Вычислим технологические коэффициенты и составим технологическую матрицу А.
a11 =
= 0,1; a12 = = 0,05; a13 = 
= 0,2.a21 =
= 0,2; a22 =; a23 = 
= 0,15.a31 =
= 0,2; a32 = 
= 0,4; a33 = 0.0,1 0,05 0,2
А = 0,3 0 0,15.
0,2 0,4 0
Составим балансовое уравнение X - AX = Y и сделаем его проверку.
100 0,1 0,05 0,2 100 45
100 - 0,3 0 0,15 · 100 = 40.
200 0,2 0,4 0 200 140
Выполним действия в левой части уравнения:
100 0,1·100 + 0,05·100 + 0,2·200 100 50 45
100 - 0,3·100 + 0·100 + 0,15·200 = 100 - 60 = 40.
200 0,2·100 + 0,4·100 + 0·200 200 60 140
Т.к. левая часть уравнения равна правой, значит, уравнение составлено верно.
1 0 0 0,1 0,05 0,2 0,9 - 0,05 - 0,2
E - A = 0 1 0 - 0,3 0 0,15 = - 0,3 1 - 0,15.
0 0 1 0,2 0,4 0 - 0,2 - 0,4 1
Вычислим матрицу полных производственных затрат B = (E - A) - 1
а) по формуле обратной матрицы:
det (E - A) = 0,7655.
0,94 0,13 0, 2075 1,23 0,17 0,27
(E - A) - 1 = 0,33 0,86 0, 195 ≈ 0,43 1,12 0,25.
0,32 0,37 0,885 0,42 0,48 1,16
б) по приближенной формуле B ≈ E + A + A2 + A3:
0,065 0,085 0,0275 0,0375 0,01425 0,02575
A2 = 0,06 0,075 0,06; A3 = 0,0405 0,027 0,2325;
0,14 0,01 0,1 0,037 0,047 0,0295
1, 2025 1,14925 0,25325 1,20 0,15 0,25
B ≈ E + A + A2 + A3 = 0,4005 1,102 1,23325 ≈ 0,40 1,10 0,23.
0,377 0,457 1,1295 0,38 - 0,46 1,13
100
Определим новый производственный план, задав YH = 50.
80
0,94 0,13 0, 2075 100 153
XH = 0,33 0,86 0, 195 50 ≈ 119.
0,32 0,37 0,885 80 159