Файл: Отчет по лабораторной работе 1 Определение коэффициента динамической вязкости жидкости методом Стокса.docx

Министерство образования и науки Российской Федерации
ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Институт заочно-вечернего обучения


Отчет по лабораторной работе № 2.1
«Определение коэффициента динамической вязкости жидкости методом Стокса»


Выполнил:

Студент группы КНбз-20-1_____________Д.А. Коровкин
№ зачетной книжки 20150787
Принял:____________________________ Кузнецова С.Ю.


Иркутск - 2021

Теоретическая часть

Различают два типа течения вязкой жидкости – ламинарное и турбулентное. Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв. Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга. При ламинарном течении жидкость можно рассматривать как совокупность отдельных слоёв, движущихся с различными скоростями. Это обусловлено тем, что при движении слоев жидкости относительно друг друга с различными скоростями между ними возникает тормозящая сила, это сила внутреннего трения или сила вязкости. Вязкость – это свойство жидкости оказывать противодействие перемещению её слоёв относительно друг друга.

Природа этих сил заключается в том, что слои жидкости, движущиеся с разными скоростями, обмениваются энергией: слои с молекулами, имеющими большую скорость, передают некоторое количество движения более медленным слоям, ускоряя их, но при этом сами подвергаются торможению. Ньютон показал, что сила внутреннего трения, действующая на средние слои, прямо пропорциональна градиенту скорости слоев в направлении, перпендикулярном течению:



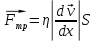
Градиент скорости – это изменение скорости двух слоёв жидкости dV на расстоянии между слоями dX. Коэффициент динамической вязкости зависит от природы жидкости и уменьшается с повышением ее температуры. Закон Ньютона определяет также силу трения, возникающую на границе между жидкостью и движущимся в ней твердым телом, например, шариком.

Метод Стокса. Стоксом был предложен метод определения , основанный на анализе движения шарика, свободно падающего в вязкой жидкости. Это возможно если плотность материала шарика _ш больше плотности жидкости _жв которой ондвижется. Характер его движения определяется тремя действующими на него силами (рис. 2): силой тяжести  , выталкивающей силой Архимеда   и силой вязкого трения  . Уравнение движения шарика из основного закона динамики в данном случае принимает вид:

 , (1)

где т – масса шарика;   – скорость его движения относительно жидкости;   – ускорение свободного падения. В проекции на ось 0х, т.е. на направление движения шарика уравнение (1) запишется:

. (2)

Особенность силы вязкого трения заключается в том, что ее величина зависит от скорости движения тела относительно жидкости. При малых скоростях эта зависимость прямо пропорциональная. В начале, при увеличении скорости тела сила трения возрастает настолько, что движение становится равномерным. Если тело имеет постоянную скорость, т.е. движение установившееся, то   и получим уравнение

. (3)

Выразим составляющие силы, входящие в уравнение (3) через параметры жидкости и шарика. Для тел сферической формы, модуль силы вязкого трения определяется формулой Стокса:

 (4)

где r – радиус шарика; V – скорость его движения относительно жидкости.

Важно отметить, что формула (4) справедлива только в случае ламинарного течения жидкости относительно шарика (скорость движения шарика должна быть небольшой), а жидкость по всем направлениям простирается безгранично, т.е. размеры сосуда, в котором находится жидкость, должны быть много больше по сравнению с размерами шарика. Условия ламинарности можно считать выполненными, если число Рейнольдса Re < Re_кр

, (5)

где ?_ж - плотность жидкости, а критическое значение числа Рейнольдса для шарика Re_кр, движущегося в жидкости можно принять равным единицы.

Выразим массу шарика через его плотность и объем

, (6)

а выражение для архимедовой силы принимает вид:

 (7)

Подставляя выражения (4), (6) и (7) в уравнение (3), и учитывая, что d=2r, после простых преобразований получим

. (8)

Ц
ель работы изучение явления внутреннего трения в жидкостях и опытное определение величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке.

Теоретическая часть

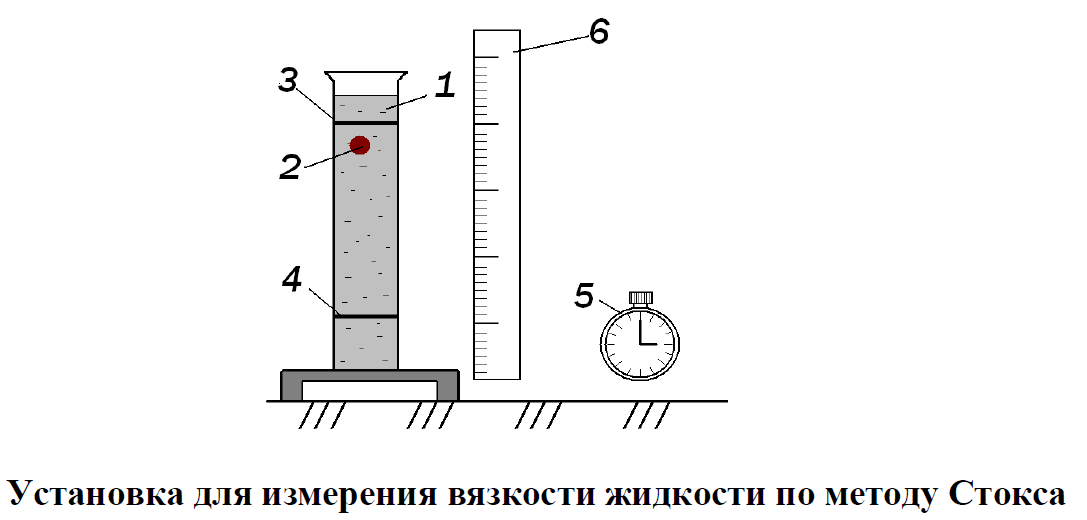
На цилиндре имеются метки 3 и 4. Расстояние между метками L можно замерить при помощи линейки 6, а диаметр шарика – при помощи микрометра. Время прохождения между метками 3 и 4 можно определить с помощью секундомера 5. Метка 3 помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости; V = const на участке L. Цилиндр закрыт пробкой с воронкой, в которую опускается шарик, двигающийся в дальнейшем примерно по оси цилиндра так, чтобы на его движение не влияли стенки. При более точных измерениях необходимо учитывать влияние размеров стеклянного цилиндра.

Эксперимент можно проводить как на физической, так и на виртуальной модели установки.

Расчетная формула:



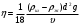
????_ж= (1,26 ± 0,01) ∙ 10³ кг/м³;

????_ш= (7,8 ± 0,1) ∙ 10³ кг/м³.
Порядок выполнения работы

1. Получить свой вариант задания и допуск к работе у ведущего преподавателя. Свой вариант (значения L и d) можно взять из таблицы в приложении по номеру зачётной книжки, в нашем случае это:

L=51-56±0,5 см=0,51-0,56м.

d=3,0-3,5±0,05мм=0,003-0,0035

2. Ознакомился с работой виртуальной лабораторной установки.

3. Провел пробные измерения для различных значений диаметра шарика d и расстояния между метками L, определяя время прохождения между метками при помощи секундомера.

4. Занес в таблицу заданные в вашем варианте значения: расстояние L_iмежду метками 3 и 4 (см. рис.3), диаметр шарика d_i и его плотность ρ_ш, а также плотность исследуемой жидкости ρ_ж.

5. Сбросив шарик в сосуд с жидкостью. В момент касания шариком верхней метки запустил секундомер, а в момент касания шариком нижней метки остановил его. Записал в таблицу показание секундомера t_i.

6. Кнопкой “СБРОС” установил нуль на табло секундомера.

7. Повторил измерения пять раз, задавая различные значения диаметра шариков d_i и расстояние L_i между метками (пункт 3 и 4).

8. Результаты опытов занесены в таблицу измерений.

Таблица 1

п/н	L, см	Δ L, см	d, мм	Δ d, мм	t, c	Δ t, c	????, м/с	????????	η, Па с	Δη, Па с	????̅, Па с
1	51	0,5	3,0	0,05	23,6	0,1	0,0216	0,05	1,48	0,5	1,5
2	56		3,0		26,7		0,0209	0,06	1,35
3	51		3,5		17,8		0,0286	0,08	1,52
4	56		3,5		19,8		0,0282	0,08	1,54
5	53		3,3		19,3		0,0274	0,08	1,41

Пример расчета для первого эксперимента таблицы 1: скорость шарика ????₁ = L₁ /t₁

????₁ = 0,51 /23,6=0,0216 м/с

????₂ = 0,56 /26,7=0,0209 м/с

????₃ = 0,51 /17,8=0,0286 м/с

????₄ = 0,56 /19,8=0,0282 м/с

????₅ = 0,53 /19,3=0,0274м/с

9. Вычислить коэффициент вязкости η для каждого из пяти опытов по рабочей формуле (7).



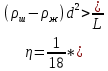
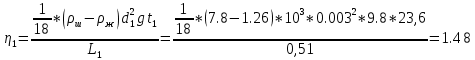(Па*с)

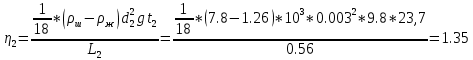(Па*с)

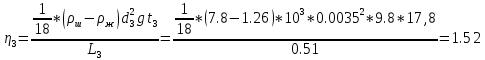(Па*с)

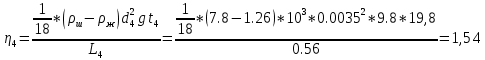(Па*с)

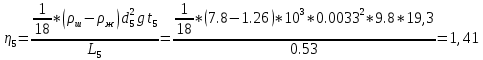(Па*с)

Число Рейнольдса











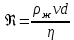
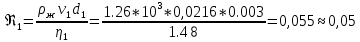
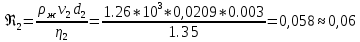
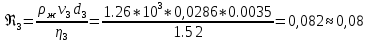
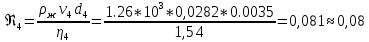
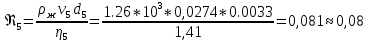
10. Найти среднее значение коэффициента вязкости 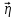по формуле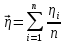





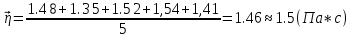
11.Определить абсолютные приборные погрешности прямых измерений (расстояния между метками ∆L, диаметра шарика ∆d, времени его падения ∆t, плотности шарика ∆ρ_ш и жидкости ∆ρ_ж), а также их относительные ошибки ε_L , ε_d , ε_ρ и ε_t.

∆L=0.5 см дано в таблице вариантов;

∆d=0.05 см дано в таблице вариантов;

∆t=0,1 с, так как секундомер цифровой, цена деления его составляет 0,1 с.






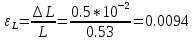
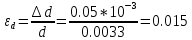
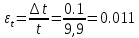
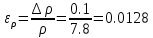
12.Оценить полную абсолютную ∆η и относительную ε погрешности.



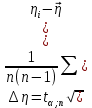
здесь количество экспериментов n = 5, доверительная вероятность α = 0,95, коэффициент Стьюдента t_0,95;5 = 2,8.

п/н	???????? , Па с	????̅, Па с	???????? − ????̅, Па с	(???????? − ????̅)2, (Па с)2
1	1,48	1,5	-0,02	0,004
2	1,35		-0,15	0,0225
3	1,52		0,02	0,004
4	1,54		0,04	0,0016
5	1,41		-0,09	0,0081
сумма				0,0402

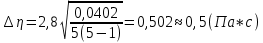
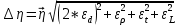
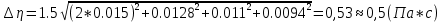
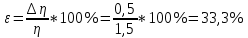
13. Записать конечный результат в виде η= 1,5± 0,5 (Па с)

14. Сравнить полученное значение η со справочными данными. Полученный экспериментальным путем диапазон значений η = 1,5 ± 0,5 (Па с) включает в себя табличное значение коэффициента вязкости для глицерина при комнатной температуре (20⁰С)

Вязкость жидкостей при атмосферном давлении:
η, 10 -3 Па· с	0°C	20°C	50°C	70°C	100°C
Ацетон	=	0.32	0.25	=	=
Бензин	0.73	0.52	0.37	0.26	0.22
Бензол	=	0.65	0.44	0.35	=
Вода	1.80	1.01	0.55	0.41	0.28
Глицерин	12100	1480	180	59	13
Керосин	2.2	1.5	0.95	0.75	0.54
Кислота уксусная	=	1.2	0.62	0.50	0.38
Масло касторовое	=	987	129	49	=
Пентан	0.28	0.24	=	=	=
Ртуть	=	1.54	1.40	=	1.24
Спирт метиловый	0.82	0.58	0.4	0.3	0.2
Спирт этиловый (96%)	1.8	1.2	0.7	0.5	0.3
Толуол	=	0.61	0.45	0.37	0.29

15. По результатам эксперимента сделали вывод: в ходе выполнения работы изучили явления внутреннего трения в жидкостях и опытным путем определили величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке.