Файл: Занятие 1 Тема. Элементы теории вероятностей, применяемые в инжиниринге качества.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое занятие №1
Тема. Элементы теории вероятностей, применяемые в инжиниринге качества.
Цель. Повышение уровня компетенций в области теории вероятностей.
Содержание работы
-
Рефлексия основных понятий теории вероятностей (20 минут).
| | Новые понятия | Содержание |
| 1 | 2 | 3 |
| 1 | Предмет теории вероятностей | изучение закономерностей, возникающих при массовых, однородных опытах |
| 2 | Стохастический эксперимент | эксперимент, результат которого заранее (до его проведения) предугадать нельзя |
| 3 | Случайное событие | явление, которое может произойти или не произойти в результате стохастического эксперимента |
| 4 | Элементарные события | события, обладающие следующими свойствами: взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий; каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А |
| 5 | Достоверное событие | такое событие, которое наступает в результате появления любого элементарного события |
| 6 | Невозможное событие | событие, не наступающее ни при каком элементарном событие |
| 7 | Сумма (или объединение)двух событий А и В | событие А+В (или АВ), происходящее тогда и только тогда, когда происходит или А, или В Р(А+В)=Р(А) + Р(В) – Р(АВ) |
| 8 | Произведение или пересечение двух событий А и В | событие АВ (или АВ), которое происходит тогда и только тогда, когда происходит и А и В |
| 9 | Несовместные события | два события являются несовместными, если их одновременное появление в опыте не возможно |
| 10 | Событие 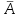 противоположно к А. противоположно к А. | если оно происходит тогда и только тогда, когда А не происходит |
| 11 | Разность событий А и В | событие А\В, происходящее тогда и только тогда, когда происходит А, но не происходит В |
| 12 | Алгебра событий | система Н событий, которая выделена в - пространство элементарных событий некоторого стохастического эксперимента) и выполняются условия: А1: Н А2: если А Н ; А3 если А и В Н А+В и АВ Н. |
| 13 | Относительная частота события А в проведенной серии экспериментов | отношение (А)=m/n числа экспериментов m, в которых событие А произошло, к количеству проведенных экспериментов n |
| 14 | Статистическое определение вероятности | если при увеличении числа опытов относительная частота события (А) стремится к некоторому фиксированному числу, то говорят, что событие А стохастически устойчиво, а это число, обозначаемое р(А) называют вероятностью события А |
| 15 | Классическая схема теории вероятностей | схема, где присутствуют стохастический эксперимент, пространство элементарных событий которого состоит из конечного (n) числа равновозможных элементов |
| 16 | Условная вероятность события В при условии, что событие А с ненулевой вероятностью произошло (р(В\А)) | отношение вероятности АВ к вероятности А 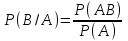 |
| 17 | Вероятность произведения | предполагая, что вероятности Р(А) или Р(В) не равны 0, можно получить следущее: Р(АВ)=Р(А)Р(В\А)=Р(В)Р(В\А) |
| 18 | Независимые случайные события А и В | такие события, для которых выполняется условие: р(АВ)=р(А) р(В) |
| 19 | Полная группа событий | совокупность событий Н1,Н2…Нn, таких, что: НiHj=, если ij, и 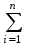 Hi = Hi = |
| 20 |  Формула Байеса Формула Байеса | 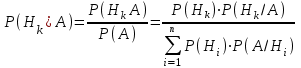 |
| 21 | Понятие случайной величины | величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента |
| 22 | Дискретная случайная величина | случайная величина, возможные значения которой образуют или конечное множество, или счетное |
| 23 | Закон распределения дискретной случайной величины | правило, по которому каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина может принять это значение |
| 24 | Функция распределения F(x) | функция, применяемая для задания случайной величины, равная вероятности того, что случайная величина примет значение, меньшее х: F(x) = p( |
| 25 | Плотность вероятности | функция, которая равна производной от функции распределения случайной величины 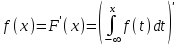 |
| 26 | Свойство плотности вероятности |
p{x1x2}= 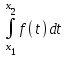 ; ;
равен единице: 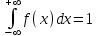 |
| 27 | Математическое ожидание дискретной случайной величины | сумма произведений всех ее возможных значений на их вероятности: 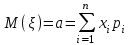 |
| 28 | Дисперсия случайной величины | математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D() = M(( - a)2) |
| 29 | Свойство дисперсии |
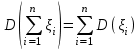 |
| 30 | Свойства математического ожидания | 1) математическое ожидание постоянной равно самой постоянной: М(С)=С; 2) постоянный множитель можно выносить за знак математического ожидания: М(С·ξ)=С·М(ξ); 3) математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий слагаемых: 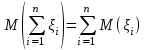 ; ;4) математическое ожидание произведения конечного числа независимых в совокупности случайных величин равно произведению математических ожиданий сомножителей: M(1...n)=M(1)...M(n) |
| 31 | Теорема Бернулли | при неограниченном увеличении числа испытаний относительная частота ν(А) события А сходится по вероятности к р(А) – вероятности его появления при одном испытании |
| 32 | Формула полной вероятности | 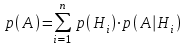 |
| 33 | Формула Бернулли | 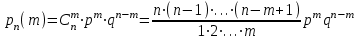 |
| 34 | Формула Пуассона | для схемы Бернулли при np<10 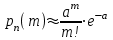 |
| 35 | Схема Бернулли | производится n независимых и однородных (одинаковых) испытаний, в результате каждого из которых может произойти событие А или ему противоположное 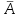 с вероятностями p и q=1-p с вероятностями p и q=1-p |
| 36 | Интегральная теорема Муавра-Лапласа | асимптотическое поведение вероятности pn(m) в схеме при больших значениях np: 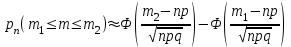 |
| 37 | Распределение Пуассона | 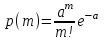 |
| 38 | Правило 3-х σ | 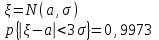 |
| 39 | Правило 2-х σ | 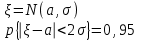 |
| 40 | Доверительный интервал | интервал, накрывающий параметр с вероятностью γ (γ – доверительная вероятность или уровень доверия) |
| 41 | Доверительный интервал для р – вероятности события А в схеме Бернулли для уровня доверия γ | 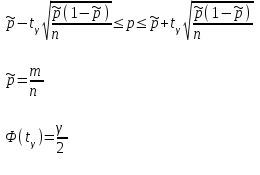 |
-
Составление макета базы знаний по теории вероятностей (10 минут). -
Решить следующие задачи по теории вероятностей (30 минут).
Задача №1
Студент выучил 25 билетов из 30. Чему равна для него вероятность вытянуть “хороший” билет, если он тянет вторым?
Задача №2
Строительная организация имеет 5 бульдозеров, вероятность безотказной работы которых в течение времени T равна 0,9. Определить вероятность того, что за время T 2 бульдозера будут нуждаться в ремонте.
Задача №3
Телевизионный кабель состоит из 400 жил. Вероятность того, что одна жила повреждена, 0,0125. Какова вероятность, что для 395 абонентов исправных жил хватит (что повреждённых жил 5).
Задача №4
Из 10 тыс. лотерейных билетов 2тыс. выигрышных. Какова вероятность, что из взятых наудачу 5 билетов хотя бы 2 окажутся выигрышными (больше одного)?
Задача №5
К магистральному водопроводу подключено 400 предприятий, каждое из которых с вероятностью 0,8 осуществляет забор воды. Найти вероятность того, что в данный момент осуществляет забор воды не менее 300 и не более350 предприятий.
Задача №6
По данным технического контроля в среднем 10% изготовляемых на заводе часов нуждается в дополнительной регулировке. Чему равна вероятность того, что из 400 изготовленных часов не менее 350 штук (больше или равно, чем 350 штук) нуждается в дополнительной регулировке.
Задача №7
Автоматическая телефонная станция получает в среднем за час 300 вызовов. Определить вероятность того, что за данную минуту она получит ровно 2 вызова.
Задача №8
Автоматическая телефонная станция получает в среднем за час 300 вызовов. Определить вероятность того, что за данную минуту она получит не более 2-х вызовов.
Задача №9
На один кубический метр грунта в среднем приходится 2 крупных камня. Найти вероятность того, что ковш экскаватора ёмкостью 3куб. м попадёт ровно 2 камня.
Задача №10
На один кубический метр грунта в среднем приходится 2 крупных камня. Найти вероятность того, что в ковш экскаватора ёмкостью 3куб. м попадёт не более 5 камней.
Задача №11
Для распределения случайных величин X, заданного таблицей, М(х) и Д(х).
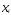 | 1 | 2 | 3 | 4 | 5 | 6 |
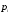 | 0,1 | 0,15 | 0,25 | 0,25 | 0,15 | 0,1 |
Задача №12
Игра состоит в том, что 2 игрока ставят на кон по 1 рублю и бросают монетку. Выигравший забирает банк (2 рубля). Чему равно математическое ожидание и среднеквадратическое отклонение выигрыша?
Задача №13
Ошибка взвешивания — случайная величина, распределённая нормально с математическим ожиданием 0 и среднеквадратическим отклонением равным 5г. Найти вероятность того, что взвешивание проведено с ошибкой, не превышающей по модулю 10г.
Задача №14
Длина куска обоев в рулоне — случайная величина, распределённая нормально с математическим ожиданием 18м и среднеквадратическим отклонением, равным 0,3м. Найти вероятность того, что длина куска в случайно выбранном рулоне обоев будет не меньше, чем 17,5м.
Задача №15
Вес груза одного вагона - случайная величина, распределённая нормально с математическим ожиданием, равным 65т и среднеквадратическим отклонением, равным 2т. Найти вероятность того, что вес груза одного вагона не превышает 70т.
Задача №16
Проверив 100 изделий в партии, обнаружили, что 8 изделий бракованных. Какова числовая оценка для вероятности случайно выбранному изделию оказаться бракованным для всей партии?
Задача №17
Проверив 100 изделий в партии, обнаружили, что 8 изделий бракованных. Какова интервальная оценка для роли брака во всей партии при уровне доверия 0,95? (Построить доверительный интервал для р).
Задача №18
Проверив 10000 изделий в партии, обнаружили, что 8 изделий бракованных. Какова интервальная оценка для доли брака во всей партии при уровне доверия 0,95? (Построить доверительный интервал для р).
Задача №19
Во сколько раз надо увеличить объём выборки, чтобы в 10 раз повысить точность оценки вероятности для доли брака?
-
Контрольный тест оценки остаточных знаний по теории вероятностей (30минут) -
Задание на дом. Оформить личную базу знаний по теории вероятностей на А4 цветными фломастерами. Провести самооценку уровня своих компетенций по теории вероятностей.
Литература
-
Ярыгин С.А., Чернова Ю.К. Вероятностно-статистичекие методы урпавления качеством. Учебное пособие. – Тольятти: ТГУ, ОАО «АВТОВАЗ», 2004, с. 14-26, 37-39.