Файл: Разработка сводного календарного плана строительства комплекса зданий.doc
Добавлен: 09.11.2023
Просмотров: 102
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
+ 
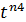+tn5) = (2150+2332+1126+926+1238) – (2045+891+730+608) = 7772 – 4274 = 3498 дн.
5. Определение рациональной очередности возведения комплекса объектов.
Для определения рациональной очередности возведения объектов в составе комплексного проекта существует множество методов. Наиболее распространенными из них являются:
1. Метод разности;
2. Метод дроби;
3. Метод расчета с помощью алгоритма Джонсона.
При организации неритмичных потоков, когда в роли захваток выступают здания (объекты), важно установить оптимальную очерёдность их возведения, обеспечивающую кратчайший срок строительства. На основании суммарной продолжительности каждого процесса на всех объектах находим поток наибольшей длительности. Этот процесс принимается за ведущий, в известной мере определяющий срок строительства. Затем по каждой строке матрицы подсчитывается время, предшествующее ведущему процессу ∑tпредш и следующее после него ∑tпосл. Результаты заносятся в первую дополнительную графу. Если ведущим потоком является первый или последний, то ∑tпредш или ∑tпосл соответственно обращаются в нуль.
Помимо ∑tпредш и ∑tпосл определяем разность между продолжительностями последнего и первого процессов с записью результатов во вторую дополнительную графу матрицы с соответствующим знаком.
а) Определение рациональной очередности возведения комплекса объектов методом разности.
В методе разности используется выражение ni-n1 – это разность между ритмом работы последней в потоке бригады и ритмом работы 1-ой бригады. Согласно методу разности, первым рекомендуется возводить объект с наибольшим значением разности.
Исходная матрица для определения рациональной очередности методом разности и матрица для оптимизации строительного потока методом разности приведены в таблицах 4 и 5 соответственно.
Таблица 4.
Исходная матрица для определения рациональной очередности методом разности
Таблица 5.
Матрица для оптимизации строительного потока методом разности
Tобщ. = (
+ 
+ 
+ 
+ 
- (
+ 
+ 
+ 
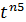) = (2241+2161+1017+843+1330) – 4274 = 7960 – 4274= 3236дн.
Вывод: Рассчитав матрицу методом разности, выявилась возможность сокращения общей продолжительности комплексного потока за счет определения рациональной очередности возведения объектов. Общая продолжительность работ, определенная методом разности меньше продолжительности работ, определенной предварительным путем.
б) Определение рациональной очередности возведения комплекса объектов методом дроби.
Согласно «правилу дроби» используется выражение:
,
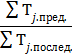где в числителе: сумма ритмов бригад на первом объекте до максимального потока; в знаменателе – сумма ритмов работы бригад после максимального потока. Первым возводится объект с минимальным значением числителя. Последним возводится объект с минимальным значением знаменателя.
Исходная матрица для определения рациональной очередности методом дроби приведена в таблице 6.
Таблица 6
Исходная матрица для определения рациональной очередности
Тi - продолжительность частного потока. 2045 дн–продолжительность наибольшего потока.
Таблица 7.
Матрица для оптимизации строительного потока методом дроби.
+tn5) = (2150+2332+1126+926+1238) – (2045+891+730+608) = 7772 – 4274 = 3498 дн.5. Определение рациональной очередности возведения комплекса объектов.
Для определения рациональной очередности возведения объектов в составе комплексного проекта существует множество методов. Наиболее распространенными из них являются:
1. Метод разности;
2. Метод дроби;
3. Метод расчета с помощью алгоритма Джонсона.
При организации неритмичных потоков, когда в роли захваток выступают здания (объекты), важно установить оптимальную очерёдность их возведения, обеспечивающую кратчайший срок строительства. На основании суммарной продолжительности каждого процесса на всех объектах находим поток наибольшей длительности. Этот процесс принимается за ведущий, в известной мере определяющий срок строительства. Затем по каждой строке матрицы подсчитывается время, предшествующее ведущему процессу ∑tпредш и следующее после него ∑tпосл. Результаты заносятся в первую дополнительную графу. Если ведущим потоком является первый или последний, то ∑tпредш или ∑tпосл соответственно обращаются в нуль.
Помимо ∑tпредш и ∑tпосл определяем разность между продолжительностями последнего и первого процессов с записью результатов во вторую дополнительную графу матрицы с соответствующим знаком.
а) Определение рациональной очередности возведения комплекса объектов методом разности.
В методе разности используется выражение ni-n1 – это разность между ритмом работы последней в потоке бригады и ритмом работы 1-ой бригады. Согласно методу разности, первым рекомендуется возводить объект с наибольшим значением разности.
Исходная матрица для определения рациональной очередности методом разности и матрица для оптимизации строительного потока методом разности приведены в таблицах 4 и 5 соответственно.
Таблица 4.
Исходная матрица для определения рациональной очередности методом разности
| «С» N | Специализированные потоки | ni-n1 | |||||
| «0» цикл | Несущ. и огр констр. | Устройство кровли и внутр. перегородок | СТ работы | ЭМ работы | Отделочные работы | ||
| N2 | 0 1  05 105 | 105 351 456 | 1546 153 1699 | 1942 125 2067 | 2260 1  042364 | 2364 195 2559 | 90 |
| N3 | 105 110 215 | 456 368 824 | 1699 161 1860 | 2067 132 2199 | 2364 110 2474 | 2559 204 2763 | 94 |
| N4 | 215 119 334 | 824 400 1224 | 1860 174 2034 | 2199 143 2342 | 2474 118 2592 | 2763 222 2985 | 103 |
| N5 | 334 79 413 | 1224 267 1491 | 2034 116 2150 | 2342 95 2437 | 2592 80 2672 | 2985 148 3133 | 69 |
| N6 | 413 196 609 | 1491 6  592150 | 2150 2  872437 | 2437 2 352672 | 2672 196 2868 | 3133 365 3498 | 169 |
Таблица 5.
Матрица для оптимизации строительного потока методом разности
| «С» N | Специализированные потоки | |||||
| «0» цикл | Несущ. и огр констр. | Устройство кровли и внутр. перегородок | СТ работы | ЭМ работы | Отделочные работы | |
| N6 | 0 1 96196 | 196 659 855 | 1466 287 1753 | 1710 235 1945 | 1906 1 962102 | 2102 365 2467 |
| N4 | 196 119 315 | 855 400 1255 | 1753 174 1927 | 1945 143 2088 | 2102 118 2220 | 2467 222 2689 |
| N3 | 315 110 425 | 1255 368 1623 | 1927 1 612088 | 2088 1 322220 | 2220 110 2330 | 2689 204 2893 |
| N2 | 425 105 530 | 1623 351 1974 | 2088 153 2241 | 2220 125 2345 | 2330 104 2434 | 2893 195 3088 |
| N5 | 530 79 609 | 1974 2 672241 | 2241 116 2357 | 2345 95 2440 | 2434 80 2514 | 3088 148 3236 |
| Полученные значения при расчёте строительного потока методом разности | ||||
| 1-2 | 2-3 | 3-4 | 4-5 | 5-6 |
| 2241 | 1550 | 1017 | 843 | 1330 |
| 1701 | 1663 | 996 | 790 | 1083 |
| 1411 | 1857 | 974 | 804 | 971 |
| 1148 | 2047 | 995 | 819 | 871 |
| 876 | 2161 | 986 | 810 | 756 |
Tобщ. = (
+ + + + - ( + + + ) = (2241+2161+1017+843+1330) – 4274 = 7960 – 4274= 3236дн.Вывод: Рассчитав матрицу методом разности, выявилась возможность сокращения общей продолжительности комплексного потока за счет определения рациональной очередности возведения объектов. Общая продолжительность работ, определенная методом разности меньше продолжительности работ, определенной предварительным путем.
б) Определение рациональной очередности возведения комплекса объектов методом дроби.
Согласно «правилу дроби» используется выражение:
, где в числителе: сумма ритмов бригад на первом объекте до максимального потока; в знаменателе – сумма ритмов работы бригад после максимального потока. Первым возводится объект с минимальным значением числителя. Последним возводится объект с минимальным значением знаменателя.
Исходная матрица для определения рациональной очередности методом дроби приведена в таблице 6.
Таблица 6
Исходная матрица для определения рациональной очередности
| «С» N | Специализированные потоки | | |||||
| «0» цикл | Несущ. и огр констр. | Устройство кровли и внутр. перегородок | СТ работы | ЭМ работы | Отделочные работы | ||
| N2 | 0 1 05 105 | 105 351 456 | 1546 153 1699 | 1942 125 2067 | 2260 1 042364 | 2364 195 2559 | 1  05577 |
| N3 | 105 110 215 | 456 368 824 | 1699 161 1860 | 2067 132 2199 | 2364 110 2474 | 2559 204 2763 | 1 10607 |
| N4 | 215 119 334 | 824 400 1224 | 1860 174 2034 | 2199 143 2342 | 2474 118 2592 | 2763 222 2985 | 1 19657 |
| N5 | 334 79 413 | 1224 267 1491 | 2034 116 2150 | 2342 95 2437 | 2592 80 2672 | 2985 148 3133 | 7 9439 |
| N6 | 413 196 609 | 1491 6 592150 | 2150 2 872437 | 2437 2 352672 | 2672 196 2868 | 3133 365 3498 | 1 961083 |
 | 609 | 2045 | 891 | 730 | 608 | 1134 | |
Тi - продолжительность частного потока. 2045 дн–продолжительность наибольшего потока.
Таблица 7.
Матрица для оптимизации строительного потока методом дроби.
| «С» N | Специализированные потоки | |||||
| «0» цикл | Несущ. и огр констр. | Устройство кровли и внутр. перегородок | СТ работы | ЭМ работы | Отделочные работы | |
| N5 | 0 7 979 | 79 267 346 | 1520 116 1636 | 1916 95 2011 | 2234 8 02314 | 2314 148 2462 |
| N2 | 79 105 184 | 346 351 697 | 1636 153 1789 | 2011 125 2136 | 2314 104 2418 | 2462 195 2657 |
| N3 | 184 110 294 | 697 368 1065 | 1789 161 1950 | 2136 132 2268 | 2418 110 2528 | 2657 204 2861 |
| N4 | 294 119 413 | 1065 400 1465 | 1950 174 2124 | 2268 143 2411 | 2528 118 2646 | 2861 222 3083 |
| N6 | 413 196 609 | 1465 6 592124 | 2124 2 872411 | 2411 2 352646 | 2646 196 2892 | 3083 365 3448 |
| Полученные значения при расчёте строительного потока методом дроби | ||||
| 1-2 | 2-3 | 3-4 | 4-5 | 5-6 |
| 2124 | 1158 | 846 | 703 | 1214 |
| 1962 | 1393 | 904 | 748 | 1170 |
| 1751 | 1608 | 940 | 776 | 1085 |
| 1472 | 1847 | 982 | 809 | 999 |
| 1265 | 2332 | 1126 | 926 | 973 |