ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание № 1.
Записать в десятичной системе следующее число
Х=11000112
Х=1*26+1*25+0*24+0*23+0*22+1*21+1*20=64+32+2+1=9910
Ответ: Х= 11000112=9910
Задание № 2.
Перевести десятичное число в заданную систему счисления
Х= 6277=_ 16
Для перевода числа 627710 в шестнадцатеричную систему счисления воспользуемся методом деления на основание. Для этого необходимо число 6277 разделить на основание системы счисления, т.е. на 16, до тех пор, пока целая часть частного не окажется меньше делителя.
| | 6277 | 16 | | | |
| | -6272 | 392 | 16 | | |
| | 5 | -384 | 24 | 16 | |
| | | 8 | -16 | 1 | |
| | | | 8 | | |
Запись шестнадцатеричного числа осуществляется с конца, в данном случае с 1.
Ответ: Х= 627710=188516
Задание № 3.
Преобразовать число в указанную систему счисления
Х= 31168=____13
Чтобы перевести целое число из любой системы счисления в другую, необходимо исходное число перевести в десятичную систему счисления, а затем последовательно делить полученное десятичное число на основание новой системы счисления.
31168=_____10
31168=3*83+1*82+1*81+6*80=161410
161410=____13
| | 1614 | 13 | |
| | -1612 | 124 | 13 |
| | 2 | -117 | 9 |
| | | 7 | |
| | | | |
Получили 161410=97213
Ответ: Х= 31168=97213
Задание № 4.
Преобразовать число в указанную систему счисления
Х= 12333124=__8
Для решения данного задания воспользуемся кодировкой. Запишем число Х=12333124 в двоичной системе счисления, для этого каждый разряд числа Х=12333124 представим в двоичном коде, а затем полученное двоичное число разобьем на группы, состоящие из трех разрядов и каждой группе определим соответствующий ей восьмеричный символ.
12333124=_____2
| 1 | 2 | 3 | 3 | 3 | 1 | 24 |
| = | = | = | = | = | = | = |
| 01 | 10 | 11 | 11 | 11 | 01 | 102 |
12333124=011011111101102
12333124=011011111101102=_______8
| 001 | 101 | 111 | 110 | 1102 |
| = | = | = | = | = |
| 1 | 5 | 7 | 6 | 68 |
12333124=011011111101102=157668
Ответ: Х= 12333124=157668
Задание № 5.
Преобразовать десятичное число в двоичное и восьмеричное
Х= 3111210=_____2=_____8
Для решения данной задачи, переведем Х=31112 из десятичной в восьмеричную систему счисления.
| | 31112 | 8 | | | | |
| | -31112 | 3889 | 8 | | | |
| | 0 | -3888 | 486 | 8 | | |
| | | 1 | -480 | 60 | 8 | |
| | | | 6 | -56 | 7 | |
| | | | | 4 | | |
| | | | | | | |
Получили 3111210=746108
746108=_____2
| 7 | 4 | 6 | 1 | 08 |
| = | = | = | = | = |
| 111 | 100 | 110 | 001 | 0002 |
Получили
746108=1111001100010002
Ответ: Х=3111210=746108=1111001100010002
Задание №6.
Преобразовать двоичное числа в восьмеричное и шестнадцатеричное
Х=100111002=_____8=_____16
Х=100111002=_____8
| 010 | 011 | 1002 |
| = | = | = |
| 2 | 3 | 48 |
Получили 100111002=2348
100111002=_______16
| 1001 | 11002 |
| = | = |
| 9 | С16 |
Получили 100111002=9С16
Ответ: 100111002=2348=9С16
Задание №7
Преобразовать восьмеричное число в шестнадцатеричное
Х=11674438=______16
Запишем число Х= 11674438 в двоичной системе счисления
| 1 | 1 | 6 | 7 | 4 | 4 | 38 |
| = | = | = | = | = | = | = |
| 001 | 001 | 110 | 111 | 100 | 100 | 0112 |
ПолучилиХ= 11674438 =0010011101111001000112
Теперь число 10011101111001000112 запишем в шестнадцатеричной системе счисления.
| 0100 | 1110 | 1111 | 0010 | 00112 |
| = | = | = | = | = |
| 4 | E | F | 2 | 316 |
Получили 10011101111001000112=4EF2316
Ответ: Х=11674438=4EF2316
Задание №8
Перевести шестнадцатеричные числа в четверичные
Х= F67A544DC16
Запишем число Х= F67A544DC16 в двоичной системе счисления
| F | 6 | 7 | A | 5 | 4 | 4 | D | C16 |
| = | = | = | = | = | = | = | = | = |
| 1111 | 0110 | 0111 | 1010 | 0101 | 0100 | 0100 | 1101 | 11002 |
ПолучилиХ= F67A544DC16=1111011001111010010101000100110111002
Теперь его запишем в четверичной системе счисления.
| 11 | 11 | 01 | 10 | 01 | 11 | 10 | 10 | 01 | 01 | 01 | 00 | 01 | 00 | 11 | 01 | 11 | 002 |
| = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = | = |
| 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | 3 | 1 | 3 | 04 |
Получили 1111011001111010010101000100110111002=3312132211101031304
Ответ: Х= F67A544DC16=3312132211101031304
Задание.
Выполнить операции сложения в дополнительном коде, с проверкой в десятичной системе счисления, для следующих исходных данных (n=8, m=0): (-27) + 45.
А=-2710, В=+4510.
Для вычисления необходимо А и В перевести в прямой код.
2710=110112, 4510=1011012
Из исходных данных видно, что В – положительное, поэтому [В]пр=[В]обр=[В]доп, а число А - отрицательное, поэтому его необходимо перевести в обратный код (по правилам перевода обратного кода):
[А]пр=0.00011011;[A]обр=1.11100100; [A]доп=1.11100101
[В]пр=0.00101101; [В]пр=[В]обр=[В]доп
Выполним сложение:
| | | | [A]доп=1.11100101 |
| | | | |
| | | | [В]доп=0.00101101 |
| | | | |
| | | | [С]доп=0.00010010 |
Проверка: А=-27, В=+45, В результате должно получиться С=+18, т.е
-2710+4510=1810
В результате сложения получилось положительное число, что подтверждает «0» в знаковом разряде, поэтому для того, чтобы проверить правильность полученного результата необходимо преобразовать полученное число [С]доп в десятичное число: [С]доп =[С]пр.
[С]пр=0.00010010=+1810
Ответ:[С]доп=0.00010010
Задача
Дана последовательность чисел, длина которой заранее неизвестна. Найдите количество четных и количество нечетных элементов последовательности. Признак конца последовательности N.
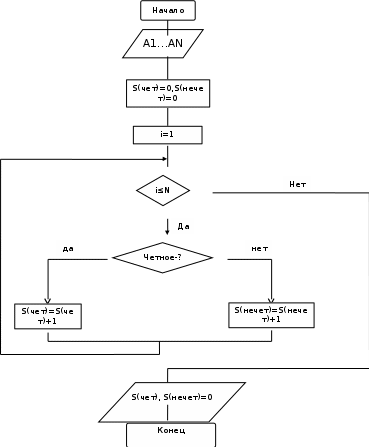
i=i+1
Пояснения к блок-схеме:
1. Проверяются условия закончилась ли последовательность чисел, если условие выполняется, тогда переходим к следующему условию.
2. Проверяются условия четное ли указанное число. Если оно четное тогда в параметре Sчет прибавляется 1, если число нечетное, тогда в параметре Sнечет прибавляется 1.
3. Проверки выполняются до тех пор, пока выполняется первое условие. Как только последовательность станет больше N, то на экран будет выведен результат подсчета четных и нечетных чисел.