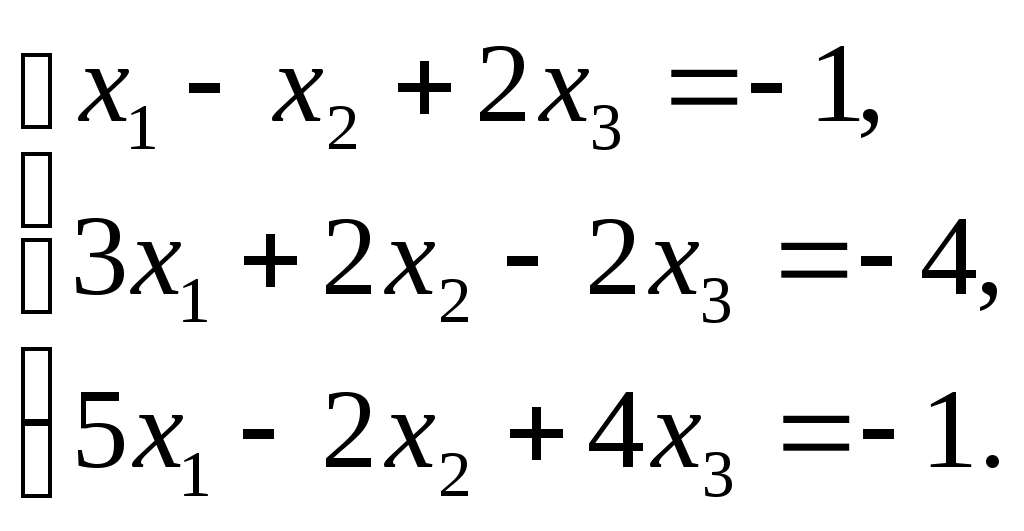
Задание №1.Решить систему линейных уравнений методом Гаусса и методом Крамера:Решение.1) Метод Гаусса.Записываем расширенную матрицу системы: 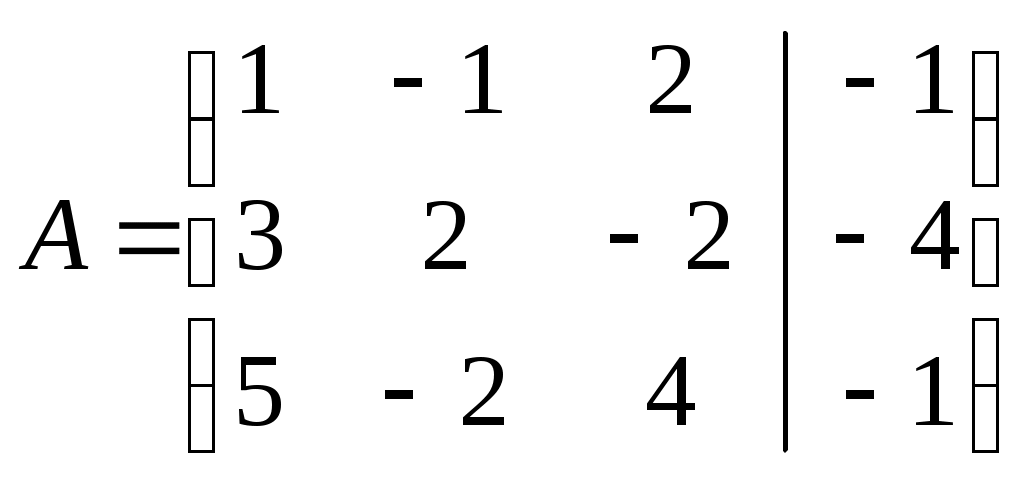.Путем элементарных операций со строками приводим ее к ступенчатому виду.Шаг первый:- вычтем из элементов второй строки соответствующие элементы первой строки, умноженные на 3;- вычтем из элементов третьей строки соответствующие элементы первой строки, умноженные на 5: 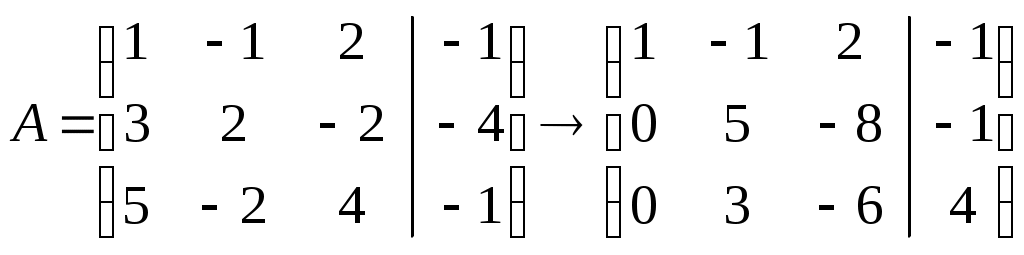.Шаг второй: вычтем из второй строки третью, умноженную на 2: 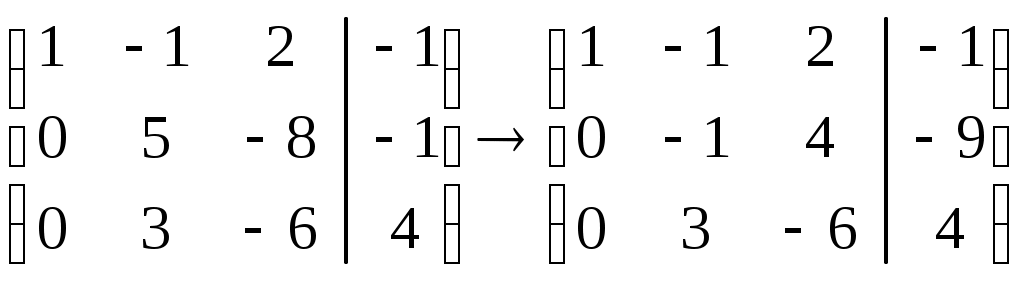.Шаг третий: прибавим к третьей строке вторую, умноженную на 3: 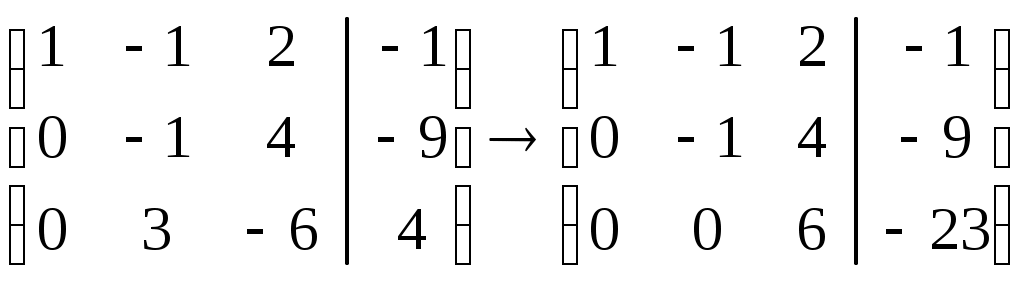.Переходим обратно к системе уравнений и последовательно находим неизвестные: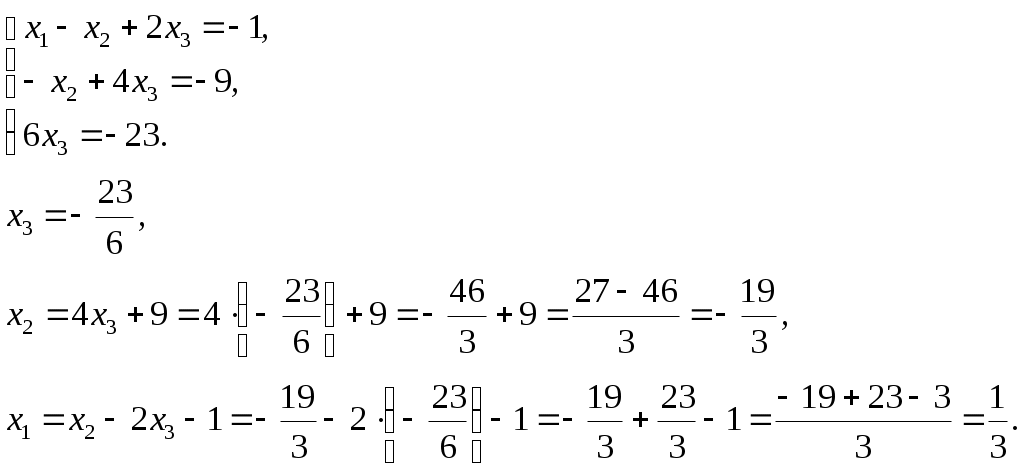Ответ: , , .2) Метод Крамера.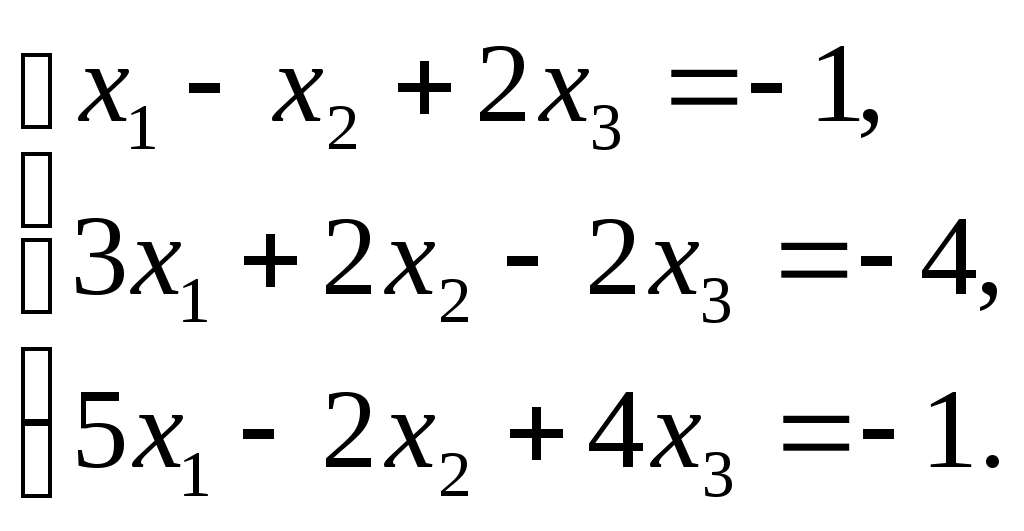Находим определитель системы: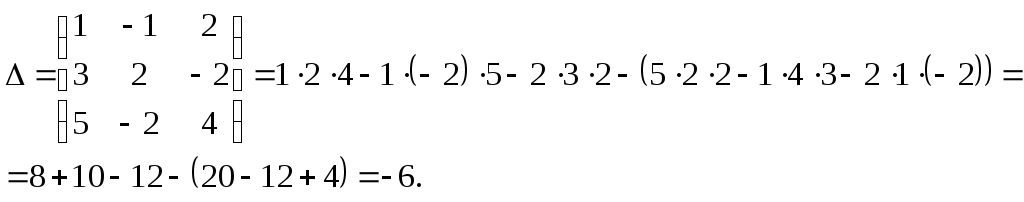Находим определители неизвестных: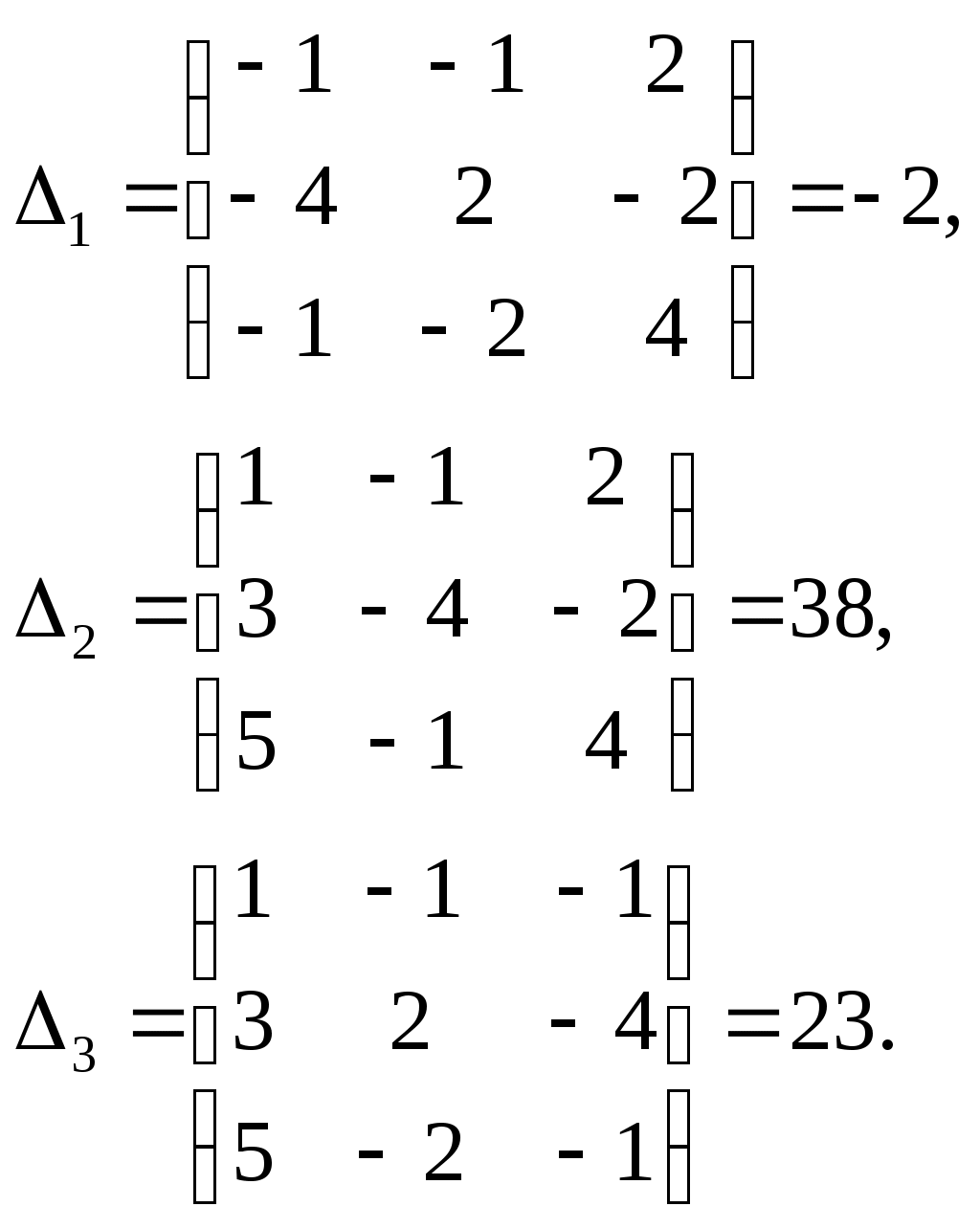По формулам Крамера находим неизвестные: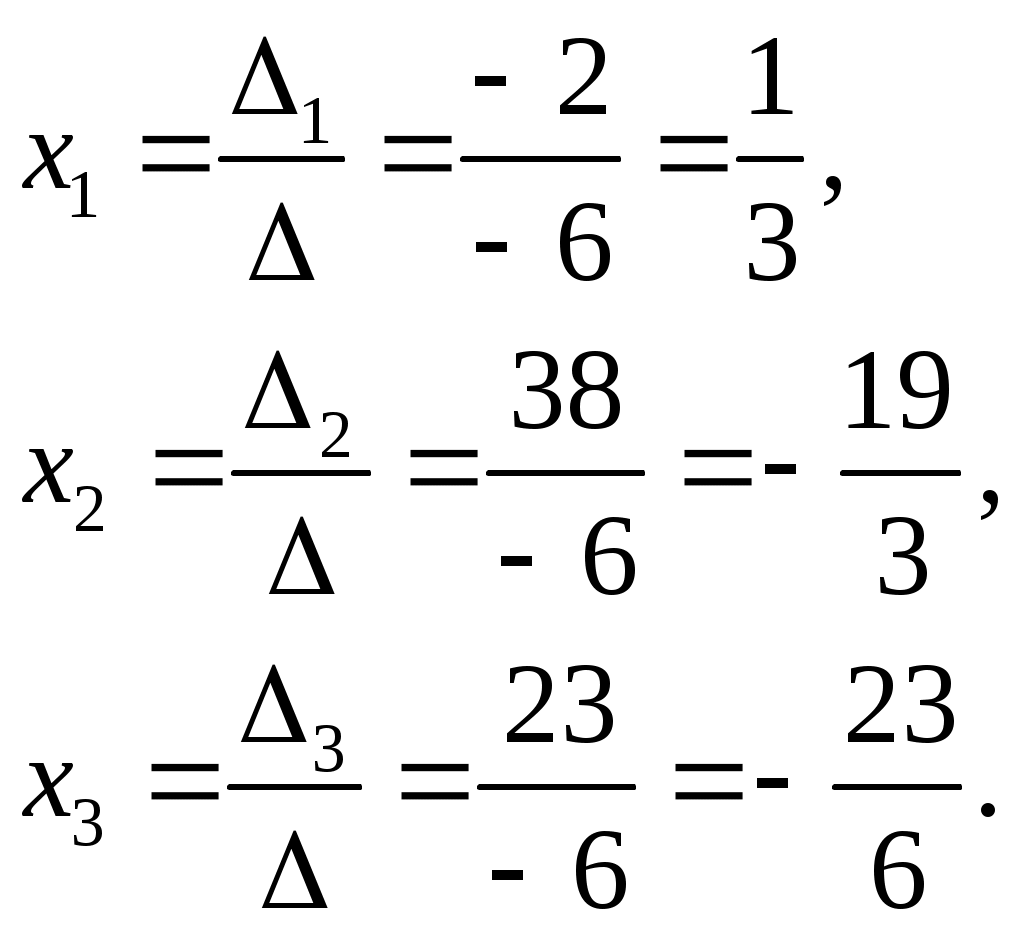Ответ: , , .Задание №2.Решить систему линейных уравнений:

---

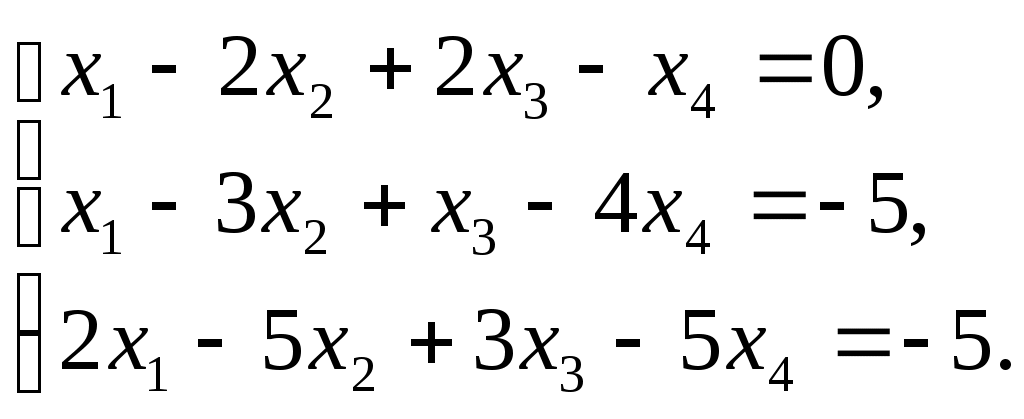
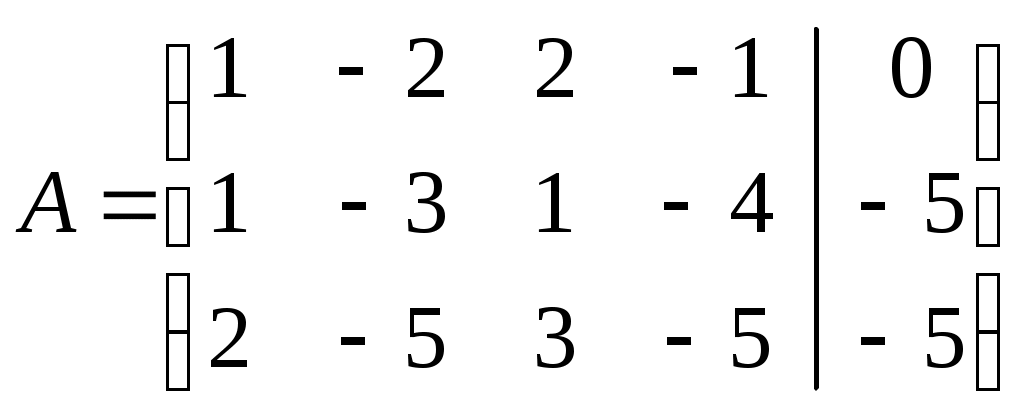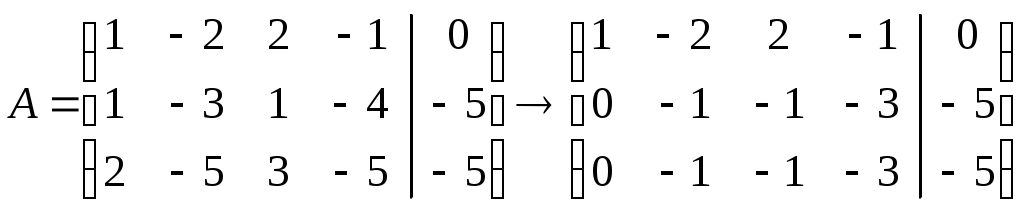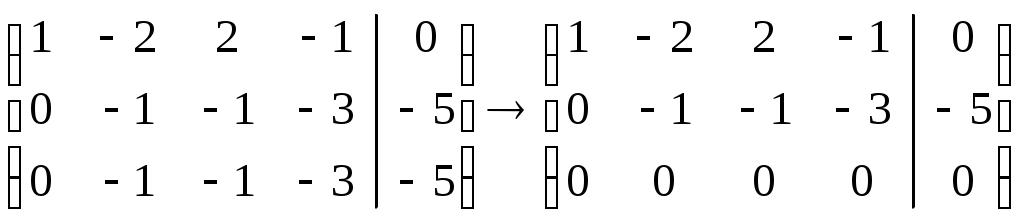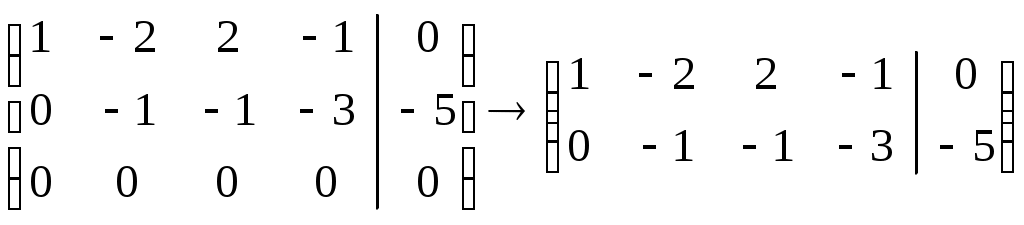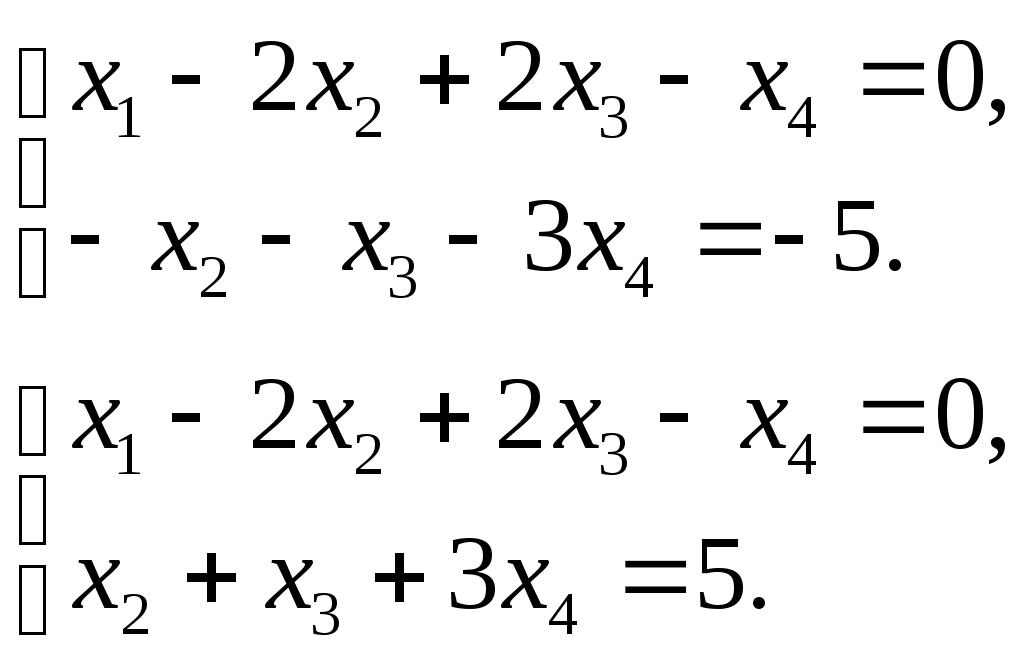
Решение.Находим общее решение системы методом Гаусса. Записываем расширенную матрицу системы: .Шаг первый: вычтем из второй строки первую; из третьей строки вычтем первую, умноженную на 2. .Шаг второй: из третьей строки вычтем вторую. .Шаг третий: отбрасываем нулевую строку. .Переходим к системе уравнений:Принимаем переменные х₁ и х₂ за базисные, а переменные х₃ и х₄ за свободные. 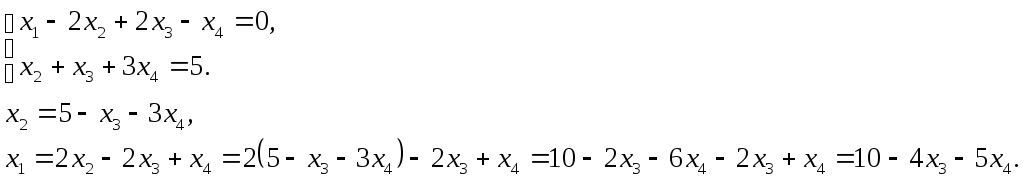Выразим базисные переменные через свободные:Общее решение имеет вид: 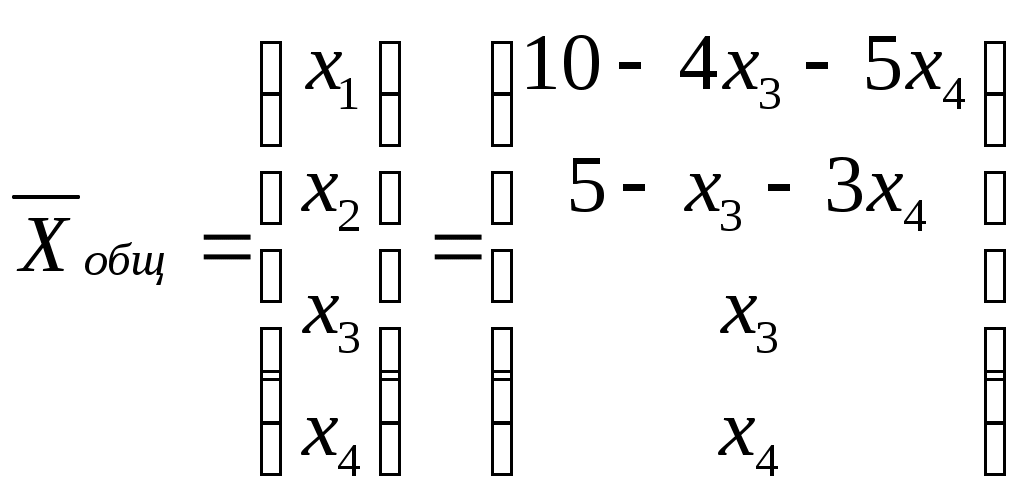.Подставляя различные значения свободных переменных, можно получить различные частные решения системы уравнений.Ответ: .

---

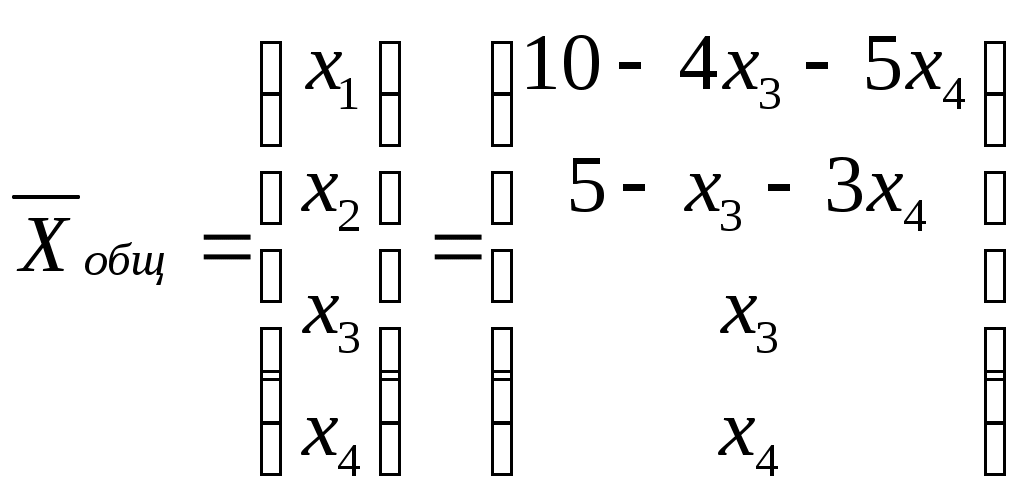Смотрите также файлы

• Первую реально работающую программируемую вычислительную машину сконструировал немец Конрад Цузе в 1941 году.docx

• Сущ.) настоящего Федерального(прил.) закона (сущ.).docx

• Повышение производительности труда прибыль от реализации продукции.docx

• Методы оценки собак по экстерьеру и конституции.docx

• Решение Определить площадь, ометаемая ветроколесом 3,14.docx