федеральное государственное бюджетное образовательное учреждение высшего образования

«Вологодский государственный университет»
Институт математики, естественных и компьютерных наук

(наименование института)

Кафедра автоматики и вычислительной техники

(наименование кафедры)

КУРСОВОЙ ПРОЕКТ
Дисциплина: «Инструментальные средства информационных систем»

Наименование темы: «Падение метеорита»

09.03.02 код направления подготовки/ специальности

. код выпускающей кафедры

___01____ регистрационный номер по журналу

Очная код формы обучения

2022 год

Руководитель	___профессор Швецов Анатолий Николаевич__
Выполнил (а) студент	_______Белов Евгений Сергеевич_______
Группа, курс	____________4Б09 ИТ-41, 4 курс______________
Дата сдачи	___________________________________________
Дата защиты Оценка по защите	___________________________________________ ___________________________________________ (подпись преподавателя)

Вологда

2022 г.

Оглавление

---

ВВЕДЕНИЕ

Каждый год на Землю падает не менее 1000 метеоритов. Однако многие из них, попадая в моря и океаны в малонаселенных районах, остаются незамеченными. Ежегодно во всем мире в музеях и научно-исследовательских учреждениях сохраняется всего от 12 до 15 метеоритов.

Происхождение метеоритов, наиболее распространенное мнение, заключается в том, что метеориты – это фрагменты малых планет. Большое количество малых планет, диаметром значительно меньше километра, образуют группу при переходе от малых планет к метеоритным телам. Столкновения малых планет в их движении вызывают непрерывный процесс их фрагментации на все меньшие и меньшие частицы, пополняя состав метеорных тел в межпланетном пространстве.

Метеориты названы в честь населенных пунктов или географических объектов, ближайших к месту падения. Многие метеориты обнаруживаются случайно и обозначаются термином "найти", в отличие от метеоритов, которые были замечены при падении и обозначаются как "падения". Один из них - тунгусский метеорит, который взорвался недалеко от реки Подкаменная Тунгуска.

Для наглядного примера последствий падения крупного метеорита на Землю создадим модель в программе NetLogo.

1 ОПИСАНИЕ МОДЕЛИ

В данном курсовом проекте необходимо разработать модель в программе Netlogo.

1. 
   Описание предметной области
   

Метеориты с большими массами тормозятся атмосферой относительно слабо и достигают поверхности с такой скоростью, что при ударе о неё они сильно изменяются, а на месте их падения остаётся кратер.

Скорость вхождения метеорита в атмосферу Земли немного превышает вторую космическую скорость 11,2 км/с, затем она снижается от торможения в атмосфере. Энергия метеорита зависит, таким образом, в основном от его массы (m), которая может изменяться в очень широких пределах.

Эта энергия тратится, во-первых, на разрушение, дробление и минеральные изменения горных пород в объеме кратера и на разрушение (вплоть до испарения) самого метеорита. Сразу нужно отметить, что при сверхзвуковом ударе размер кратера окажется значительно большим, чем размер самого метеорита, поэтому затраты энергии будут связаны с образованием кратера, а не с изменением самого метеорита. Во-вторых, часть начальной энергии переходит в кинетическую энергию выбрасываемых из кратера горных пород. В-третьих, есть еще расход на энергию звуковых волн, уходящих в глубь Земли и в атмосферу. Есть, наконец, тепловая энергия, т.е. энергия, уходящая на нагревание, а при мощных взрывах – на частичное плавление и даже испарение горных пород.

---

Приближаясь к поверхности земли, плотность воздуха увеличивается, сопротивление тела увеличивается, и оно либо останавливается практически на любой высоте, либо продолжается на своем пути до прямого столкновения с землей. В этом случае большие тела часто разбиваются на несколько частей, каждая из которых падает на землю отдельно. Во время резкого замедления космической массы над Землей сопровождающие ее ударные волны продолжают свое движение к поверхности Земли, отражаются от нее и вызывают возмущения в нижних слоях атмосферы, а также на поверхности Земли.
1.2 Аналоги данной модели

В библиотеке NetLogo есть одна похожая модель, которая показывает пожар в лесу, но данная модель обладает немного другом функционалом. Она показывает годичный цикл лесного пожара, который может случайно вспыхнуть в любой точке, и его влияние на животных и деревья. Также в этой модели довольно слабо проработана биосфера леса, так как в ней не отображена естественная жизнь животных, а значит, и того, как пожар влияет на неё.

Модель лесного пожара представлена на рисунке 1.1.



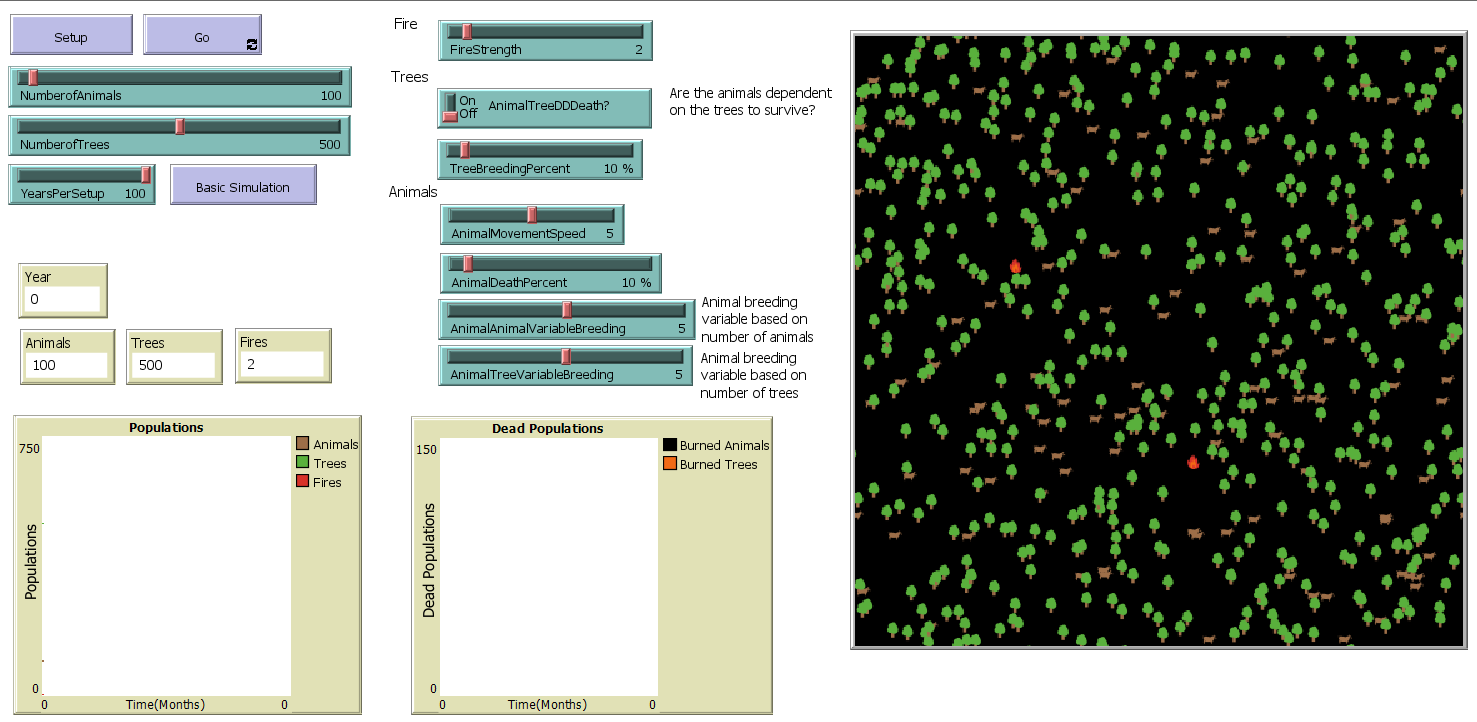
Рисунок 1.1 – Модель Fire in the forest

1.3 Математическая модель

Практически вся энергия метеорита уходит в конечном счёте именно на нагревание горных пород, пройдя перед этим через другие механические формы. Оговорка «практически» связана с изменением в результате столкновения с метеоритом скорости движения всей Земли и скорости её вращения. Они ничтожны даже при столкновении Земли с большим астероидом.

Расход энергии Е₁ на разрушение пород пропорционален объёму кратера. Будем считать объём равным примерно R. Энергия разрушения есть объём, умноженный на предел прочности горных пород у_m, то есть

E₁ = y_m*R.

При оценках размеров кратеров будем считать у_m равным пределу прочности осадочных пород у_m =10000000 Н/м. В качестве порядка величины плотности примем:

r =3 x 10 кг/см.

Второй возможный расход энергии Е₂ идёт на выброс горных пород из кратера. Перемещение большей части массы при образовании кратера происходит на расстоянии порядка его радиуса R. Для такого перемещения масс в поле тяжести начальная скорость разлёта U₀ должна по порядку величины быть равной U₀ = v*gR. Полная масса выброшенных из кратера пород есть mk = r*R*і. Поэтому затраты на кинетическую энергию горных пород, или, другими словами, затраты на выброс, есть

---

E₂ = m*k*x*U₀ = r*g*R_i.

Энергетические расходы на звуковые волны E₃ всегда бывают малы по сравнению с E₁ и E₂. Физическая причина этого состоит в том, что при любом сверхзвуковом столкновении сначала возникает ударная волна. Именно ударная волна на своём пути производит все описанные явления: и разрушения, и ускорение вещества. Интересно, что даже при наклонном падении метеорита образуется почти симметричный кратер – все кратеры одного размера схожи между собой. Это происходит потому, что ударная волна распространяется от точки удара практически одинаково, независимо от его направления. Только тогда, когда основная энергия ударной волны окажется израсходованной, когда сжатие в волне станет слабым, а скорость – равной скорости звука, она переходит в обычную акустическую, звуковую волну. Волна является ударной примерно в объёме кратера, а звук убегает с малым затуханием на большие расстояния.

Итак, главные первичные энергетические затраты есть Е 1 и Е 2. Теперь напишем приближённое уравнение энергетического баланса при падении метеорита. Оно позволит определить порядок величины радиуса кратера:

Е = у_m*R*і + r*g*R_i.

Два слагаемых уравнения по-разному зависят от радиуса кратера R. Поэтому при малых энергиях для малых кратеров главным оказывается первый член, а для больших – второй. Кратеры первого типа называют ПРОЧНОСТНЫМИ, а второго – ГРАВИТАЦИОННЫМИ. Масса метеорита, образующего кратер критического радиуса, по порядку величины есть m_o = 3000000 кг.

Падение таких и больших метеоритов – достаточно редкое событие, но поскольку след его остается на земной поверхности на времена геологических масштабов, то общее число обнаруженных на сегодня гравитационных кратеров около ста

2 РАЗРАБОТКА И РЕАЛИЗАЦИЯ ПРОГРАММНОЙ МОДЕЛИ

За основу была взята модель распространения пожара. Данная модель имитирует распространение огня среди леса. В моей модели метеорит падает, образуя кратер, сжигая затем случайным образом один объект за тик, и распространяется на его место. Так же в модели возможно отключить падение метеорита с целью посмотреть и сравнить поведение агентов в обычной ситуации

В модели представлены рычажки, отвечающие за генерацию деревьев, кроликов, и размер метеорита. Рычажок “initial-number-rabbit” отвечает за общее начальное количество кроликов, “initial-number-trees” – за начальное количество деревьев, а “initial-meteor-size” – за размер метеорита.

---

На рисунке 2.1 красным выделены эти рычажки в модели.



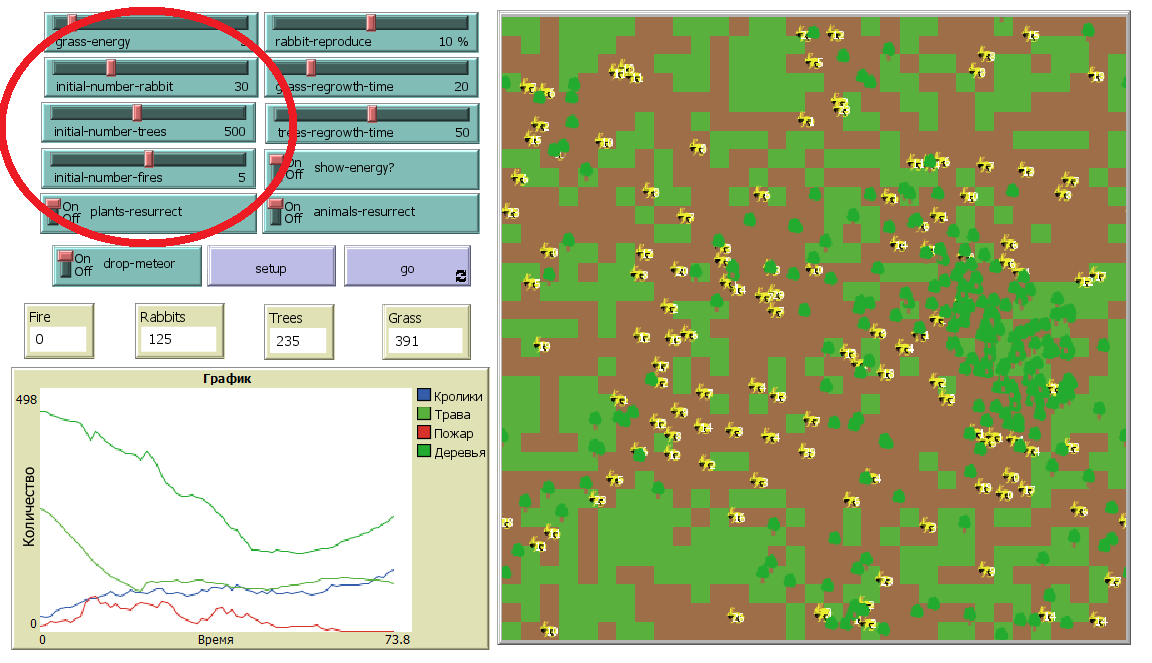
Рисунок 2.1 – Генерация
Также добавим рычажок “grass-energy”, отвечающий за то, сколько энергии будут получать кролики, поедая траву. (рисунок 2.2).



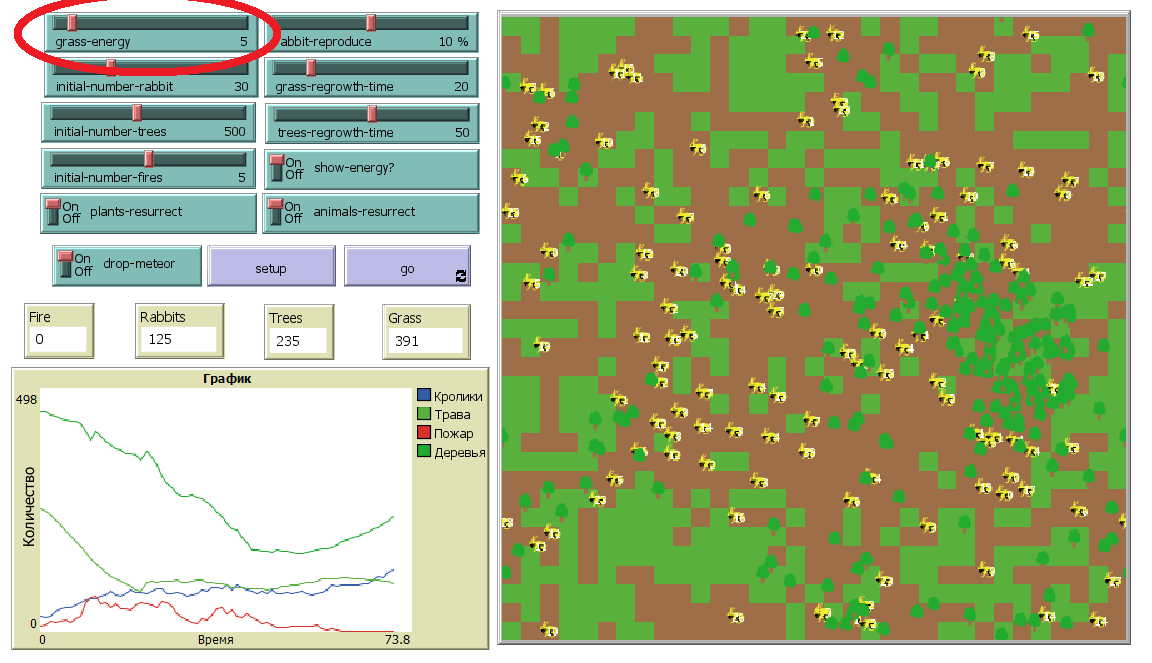
Рисунок 2.2 – Количество энергии от поедания травы
Рычажки “rabbit-reproduce”, “grass-regrowth-time”, “trees-regrowth-time” отвечают за время, необходимое для размножения кроликов, травы и деревьев соответственно. (рисунок 2.3).



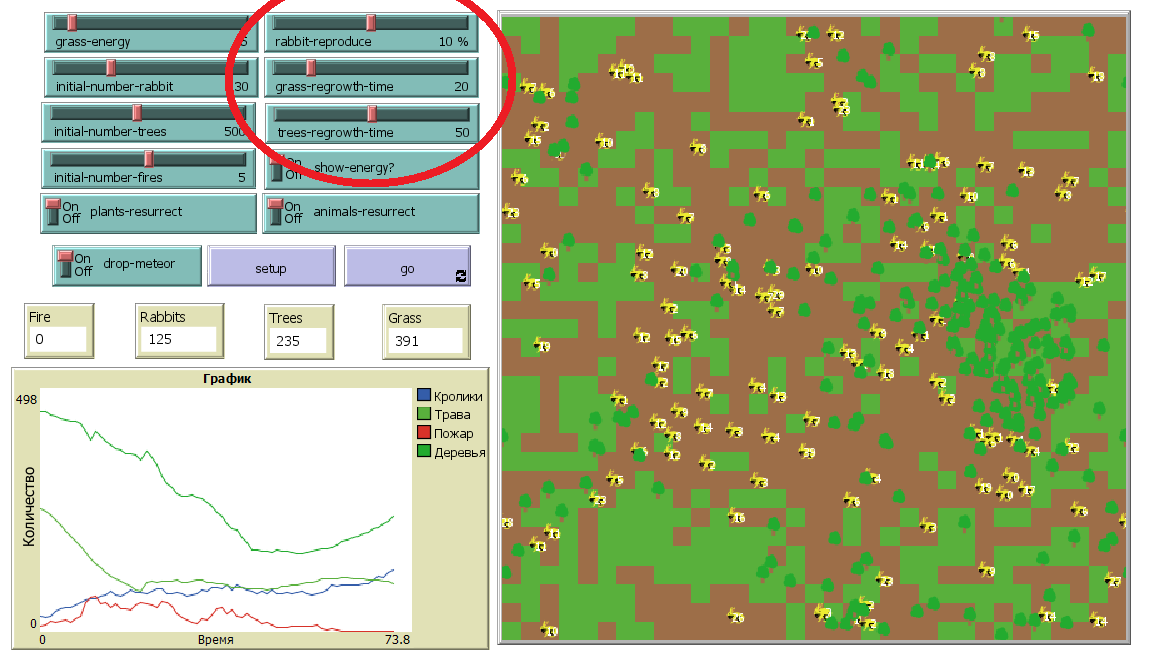
Рисунок 2.3 – Время для размножения
Далее по порядку идут переходы. “show-energy” позволяет видеть или не видеть количество энергии у кроликов, “plants-resurrect” и “animals-resurrect” включает и отключает возможность размножения для растений и кроликов соответственно, “drop-meteor” позволяет включить или отключить падение метеорита. На рисунке 2.4 они выделены красным.



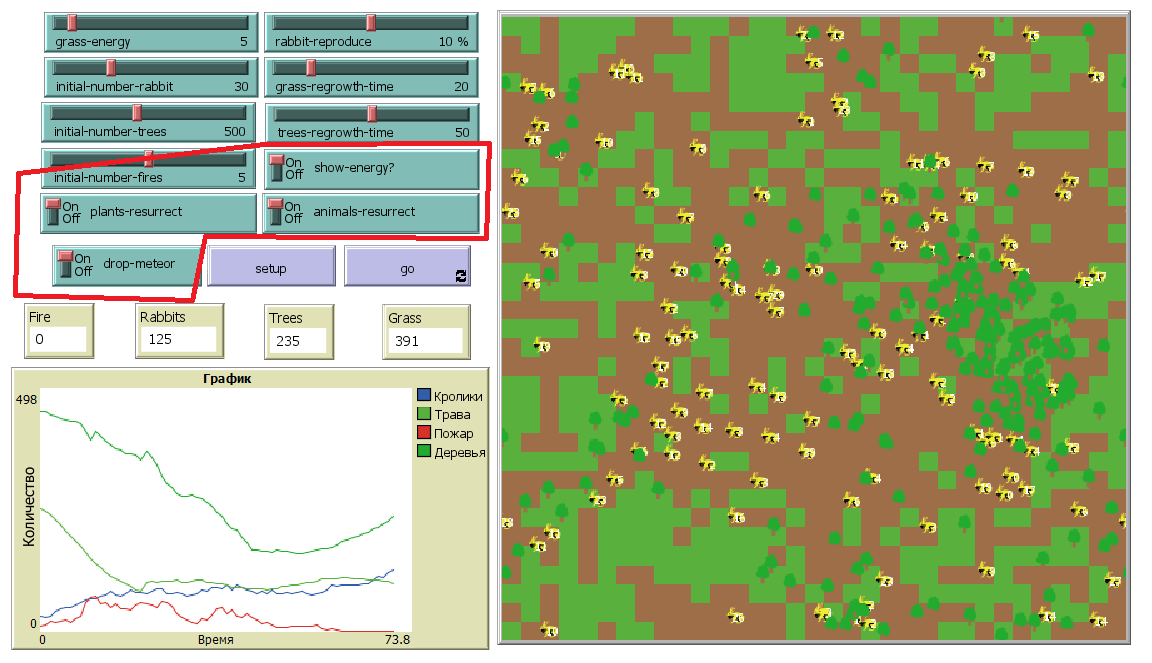
Рисунок 2.4 – Переходы
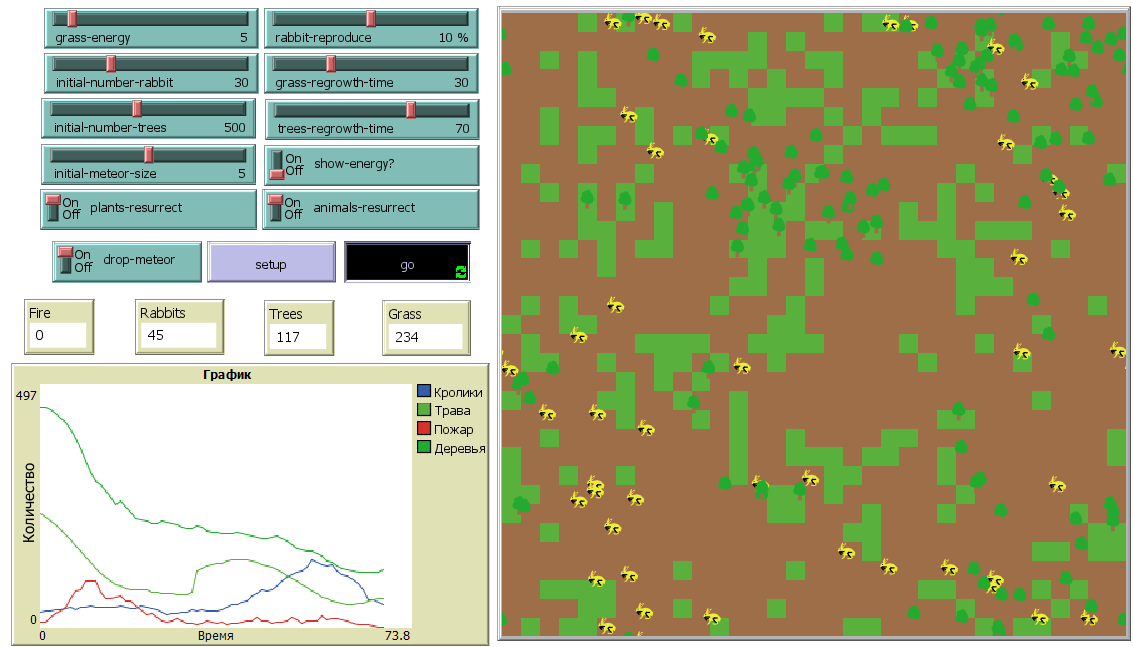
Также необходимо добавить график и численное отображение, которые будут количество животных и растений и размер пожара. (рисунок 2.5).



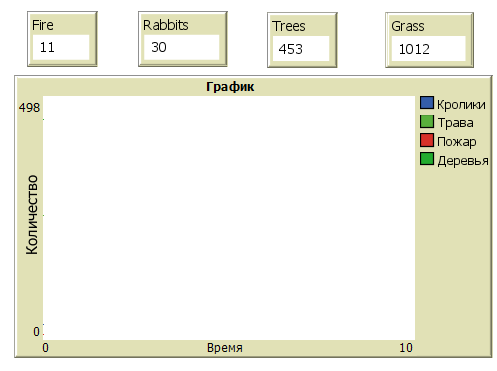
Рисунок 2.5 – График и экраны

3 ИССЛЕДОВАНИЕ РАЗРАБОТАННОЙ ПРОГРАММНОЙ МОДЕЛИ

В этом разделе проведем исследование нашей программной модели.

3.1 Первая серия экспериментов

Проведем исследование модели, меняя размер метеорита.

Первый эксперимент.



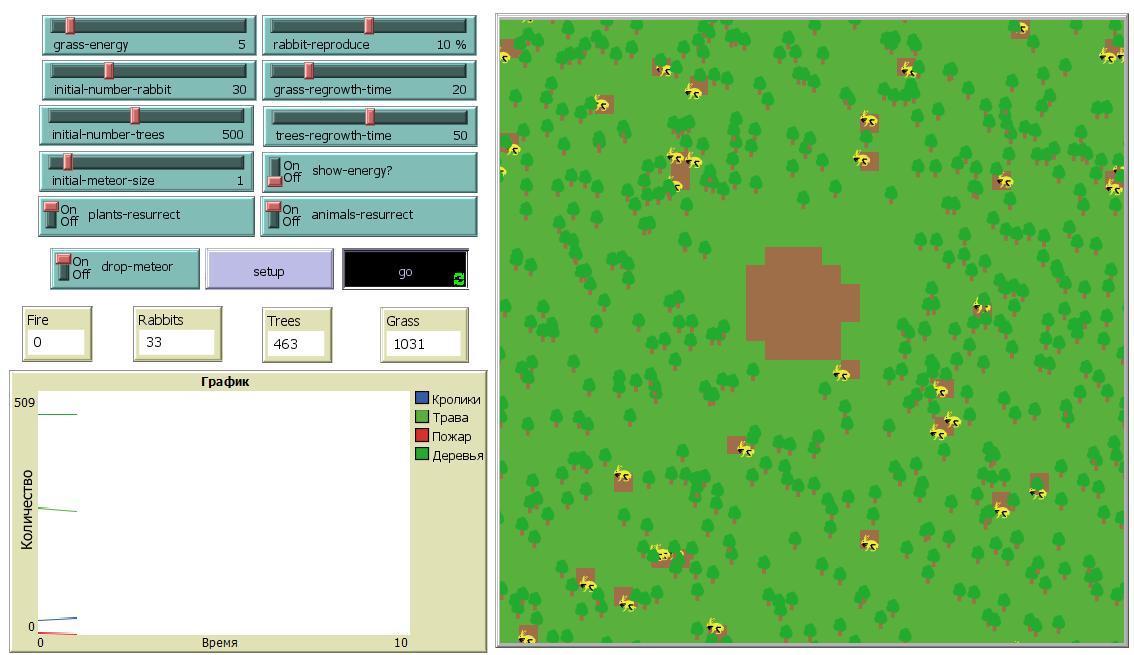
При минимальном размере метеорита остаётся небольшой кратер, пожар не распространяется, 37 деревьев и трава уничтожены только за счёт ударной волны.

Второй эксперимент.



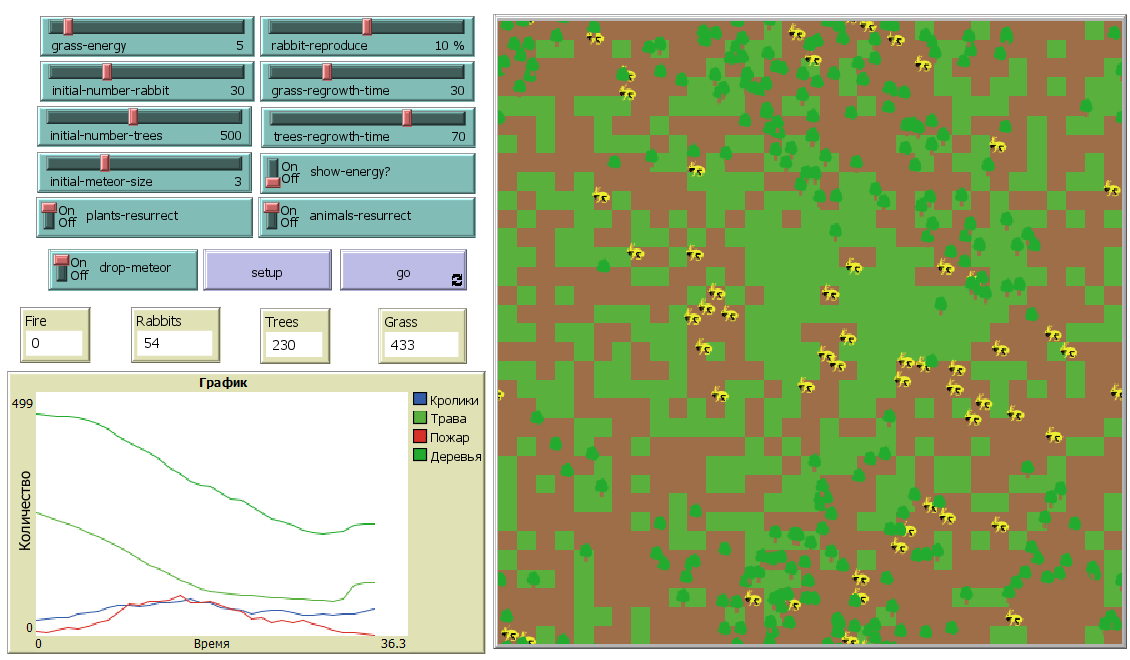
Пожар сжёг половину леса, кратер зарос травой. Ударной волной было уничтожено примерно 40 деревьев.

Третий эксперимент.

---

Смотрите также файлы

• 1. Основными принципами философии сестринского дела в России являются уважение к.docx

• Контрольная работа по дисциплине Макроэкономика.docx

• Варианты 1 Усилие есть необходимое условие нравственного совершенствования.docx

• 1. История развития статистики 5 История становления статистики в России 6 Хронология развития 8.docx

• Физическая культура и физические упражнения могут сыграть значительную роль в профилактике профессиональных заболеваний юриста.docx