Файл: Методы расчета электрических цепей постоянного тока.docx
ВУЗ: Казахская академия транспорта и коммуникаций им. М. Тынышпаева
Категория: Лекция
Дисциплина: Физика
Добавлен: 03.02.2019
Просмотров: 380
Скачиваний: 7
Метод контурных токов.
При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа.
Следовательно, метод контурных токов более экономен при вычислительной работе, чем метод на основе законов Кирхгофа (в нем меньше число уравнений).
Вывод основных расчетных уравнений приведем применительно к схеме рис. 2.12, в которой два независимых контура.
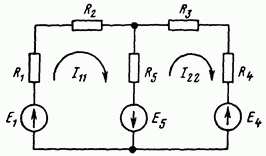
Рис. 2.12
Положим,
что в левом контуре по часовой стрелке
течет контурный ток ![]() а
в правой (также по часовой стрелке) —
контурный ток
а
в правой (также по часовой стрелке) —
контурный ток ![]() Для
каждого контура составим уравнения по
второму закону Кирхгофа. При этом учтем,
что по смежной ветви (с сопротивлением
Для
каждого контура составим уравнения по
второму закону Кирхгофа. При этом учтем,
что по смежной ветви (с сопротивлением ![]() )
течет сверху вниз ток —
)
течет сверху вниз ток — ![]() Направления
обхода контуров примем также по часовой
стрелке.
Направления
обхода контуров примем также по часовой
стрелке.
Для первого контура
![]()
Для второго контура
![]()
В
уравнении (б) множитель при токе ![]() являющийся
суммой сопротивлений первого контура,
обозначим через
являющийся
суммой сопротивлений первого контура,
обозначим через ![]() множитель
при токе
множитель
при токе ![]() (сопротивление
смежной ветви, взятое со знаком минус)
— через
(сопротивление
смежной ветви, взятое со знаком минус)
— через ![]()
Перепишем эти уравнения следующим образом:
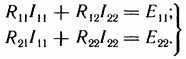
Здесь
![]()
где ![]() —
полное или собственное сопротивление
первого контура;
—
полное или собственное сопротивление
первого контура; ![]() —
сопротивление смежной ветви между
первым и вторым контурами, взятое со
знаком минус;
—
сопротивление смежной ветви между
первым и вторым контурами, взятое со
знаком минус; ![]() —
контурная ЭДС первого контура, равная
алгебраической сумме ЭДС этого контура
(в нее со знаком плюс входят те ЭДС,
направления которых совпадают с
направлением обхода контура);
—
контурная ЭДС первого контура, равная
алгебраической сумме ЭДС этого контура
(в нее со знаком плюс входят те ЭДС,
направления которых совпадают с
направлением обхода контура); ![]() полное
или собственное сопротивление второго
контура;
полное
или собственное сопротивление второго
контура; ![]() —
сопротивление смежной ветви между
первым и вторым контурами, взятое со
знаком минус;
—
сопротивление смежной ветви между
первым и вторым контурами, взятое со
знаком минус; ![]() —
контурная ЭДС второго контура.
—
контурная ЭДС второго контура.
В
общем случае можно сказать, что
сопротивление смежной ветви
между ![]() и
и ![]() -контурами
-контурами ![]() входит
в уравнение со знаком минус, если
направления контурных токов
входит
в уравнение со знаком минус, если
направления контурных токов ![]() вдоль
этой ветви встречны, и со знаком плюс,
если направления этих токов согласны.
вдоль
этой ветви встречны, и со знаком плюс,
если направления этих токов согласны.
Если в схеме больше двух контуров, например три, то система уравнений выглядит следующим образом:
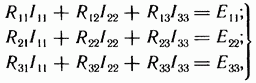
или в матричной форме
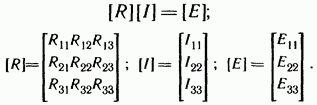
Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например по часовой стрелке.
В результате решения системы уравнений какой-либо один или несколько контурных токов могут оказаться отрицательными.
В
ветвях, не являющихся смежными между
соседними контурами (например, в ветви
с сопротивлениями ![]() схемы
рис. 2.12), найденный контурный ток является
действительным током ветви. В смежных
ветвях через контурные токи определяют
токи ветвей. Например, в ветви с
сопротивлением
схемы
рис. 2.12), найденный контурный ток является
действительным током ветви. В смежных
ветвях через контурные токи определяют
токи ветвей. Например, в ветви с
сопротивлением ![]() протекающий
сверху вниз ток равен разности —
протекающий
сверху вниз ток равен разности — ![]()
Если
в электрической цепи имеется ![]() независимых
контуров, то число уравнений тоже
равно
независимых
контуров, то число уравнений тоже
равно ![]() .
.
Общее
решение системы ![]() уравнений
относительно тока
уравнений
относительно тока ![]()
![]()
где
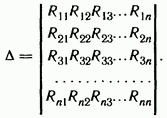
— определитель системы.
Алгебраическое
дополнение ![]() получено
из определителя Д путем вычеркивания
получено
из определителя Д путем вычеркивания ![]() столбца
и
столбца
и ![]() строки
и умножения полученного определителя
на
строки
и умножения полученного определителя
на ![]()
Если
из левого верхнего угла определителя
провести диагональ в его правый нижний
угол (главная диагональ) и учесть,
что ![]() то
можно убедиться в том, что определитель
делится на две части, являющиеся
зеркальным отображением одна другой.
Это свойство определителя называют
симметрией относительно главной
диагонали. В силу симметрии определителя
относительно главной диагонали
то
можно убедиться в том, что определитель
делится на две части, являющиеся
зеркальным отображением одна другой.
Это свойство определителя называют
симметрией относительно главной
диагонали. В силу симметрии определителя
относительно главной диагонали![]()
Составлению
уравнений по методу контурных токов
для схем с источниками тока присущи
некоторые особенности. В этом случае
полагаем, что каждая ветвь с источником
тока входит в контур, замыкающийся через
ветви с источниками ЭДС и сопротивлениями,
и что токи в этих контурах известны и
равны токам соответствующих источников
тока. Уравнения составляют лишь для
контуров с неизвестными контурными
токами. Если для схемы рис. 2.14, а принять,
что контурный ток ![]() течет
согласно направлению часовой стрелки
по первой и второй ветвям, а контурный
ток
течет
согласно направлению часовой стрелки
по первой и второй ветвям, а контурный
ток ![]() замыкается
также по часовой стрелке по второй и
третьей ветвям, то, согласно методу
контурных токов, получим только одно
уравнение с неизвестным током
замыкается
также по часовой стрелке по второй и
третьей ветвям, то, согласно методу
контурных токов, получим только одно
уравнение с неизвестным током ![]()
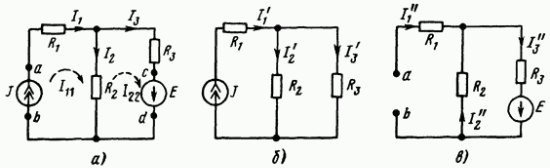
Рис. 2.14
Метод узловых потенциалов.
Ток в любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов.
Допустим,
что в схеме ![]() узлов.
Так как любая (одна) точка схемы может
быть заземлена без изменения
токораспределения в ней, один из узлов
схемы можно мысленно заземлить, т. е.
принять потенциал его равным нулю. При
этом число неизвестных уменьшается
с
узлов.
Так как любая (одна) точка схемы может
быть заземлена без изменения
токораспределения в ней, один из узлов
схемы можно мысленно заземлить, т. е.
принять потенциал его равным нулю. При
этом число неизвестных уменьшается
с ![]() до
до ![]()
Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Кирхгофа. В том случае, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономным, чем метод контурных токов.
Обратимся
к схеме рис. 2.24, которая имеет довольно
большое число ветвей (И) и сравнительно
небольшое число узлов (4). Если узел 4
мысленно заземлить, т. е. принять ![]() то
необходимо определить потенциалы только
трех узлов:
то
необходимо определить потенциалы только
трех узлов: ![]() Для
единообразия в обозначениях условимся
в § 2.22 токи писать с двумя индексами:
первый индекс соответствует номеру
узла, от которого ток утекает, второй
индекс — номеру узла, к которому ток
подтекает. Проводимости ветвей также
будут снабжаться двумя индексами.
Для
единообразия в обозначениях условимся
в § 2.22 токи писать с двумя индексами:
первый индекс соответствует номеру
узла, от которого ток утекает, второй
индекс — номеру узла, к которому ток
подтекает. Проводимости ветвей также
будут снабжаться двумя индексами.
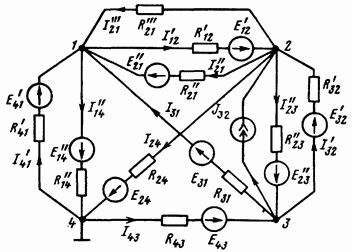
Рис. 2.24
Необходимо заметить, что эти проводимости не имеют ничего общего с входными и взаимными проводимостями ветвей, которые рассматривались в § 2.15.
В соответствии с обозначениями токов на рис. 2.24 составим уравнение по первому закону Кирхгофа для первого узла:
![]()
или
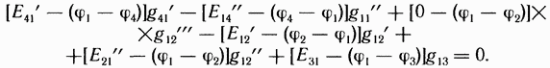
Перепишем последнее уравнение следующим образом:
![]()
где
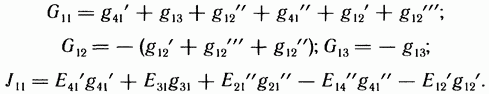
Подобные
же уравнения могут быть записаны и для
остальных узлов схемы. Если схема
имеет ![]() узлов,
то ей соответствует система из
узлов,
то ей соответствует система из ![]() уравнений:
уравнений:
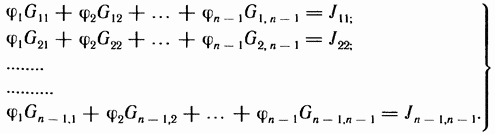
В
общем случае ![]() —
сумма проводимостей ветвей, сходящихся
в узле
—
сумма проводимостей ветвей, сходящихся
в узле ![]() —
сумма проводимостей ветвей, непосредственно
соединяющих узлы
—
сумма проводимостей ветвей, непосредственно
соединяющих узлы ![]() взятая
со знаком минус. Если между какими-либо
двумя узлами ветвь отсутствует, то
соответствующая проводимость равна
нулю. В формировании узлового
тока
взятая
со знаком минус. Если между какими-либо
двумя узлами ветвь отсутствует, то
соответствующая проводимость равна
нулю. В формировании узлового
тока ![]() -узла
-узла ![]() участвуют
те ветви, подходящие к этому узлу, которые
содержат источники ЭДС и (или) тока. Если
ЭДС
участвуют
те ветви, подходящие к этому узлу, которые
содержат источники ЭДС и (или) тока. Если
ЭДС ![]() -ветви
направлены к
-ветви
направлены к ![]() -узлу,
то ее вклад в формирование
-узлу,
то ее вклад в формирование ![]() равен
равен ![]() ,
а если эта ЭДС направлена от
,
а если эта ЭДС направлена от ![]() -узла,
то ее вклад составляет —
-узла,
то ее вклад составляет — ![]() .
Если к
.
Если к ![]() -узлу
подтекает ток от источника тока, то он
должен быть введен в
-узлу
подтекает ток от источника тока, то он
должен быть введен в ![]() со
знаком плюс, если этот ток от источника
тока утекает, то он должен входить в
со
знаком плюс, если этот ток от источника
тока утекает, то он должен входить в ![]() со
знаком минус. После решения системы
(2.22) относительно потенциалов определяют
токи в ветвях по закону Ома для участка
цепи, содержащего ЭДС.
со
знаком минус. После решения системы
(2.22) относительно потенциалов определяют
токи в ветвях по закону Ома для участка
цепи, содержащего ЭДС.
В том случае, когда в схеме имеются два узла, соединенных ветвью, в которой имеется ЭДС, а сопротивление ее равно нулю, перед составлением системы уравнений по методу узловых потенциалов один из этих узлов рекомендуется устранить в соответствии с приемом, рассмотренным в §2.24.
Система уравнений (2.22) может быть представлена в матричной форме записи:
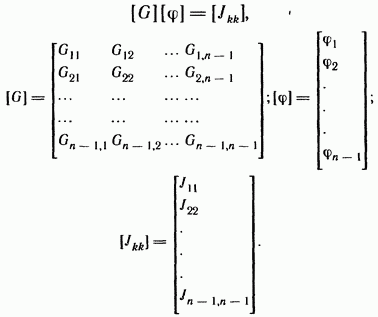 (2.22а)
(2.22а)
Ее решение
![]() (2.22б)
(2.22б)
Еще Максвеллом было установлено, что распределение токов в электрических цепях всегда происходит так, что тепловая функция системы
![]()
минимальна.
Коэффициент 1/2 обусловлен тем, что при
двойном суммировании мощность каждой
ветви учитывается дважды. Доказательство
основано на том, что совокупность
уравнений (2.22) является совокупностью
условий минимума функции Р, т. е.
совокупностью условии — ![]() и
т. д.
и
т. д.
Так
как вторые производные ![]() положительны,
то это и является доказательством
минимума тепловой функции Р.
положительны,
то это и является доказательством
минимума тепловой функции Р.
Пример
23. Найти токи в ветвях схемы рис. 2.24 и
сделать проверку по второму закону
Кирхгофа. Дано: ![]() .
Источник тока, включенный между узлами
3 и 2, дает ток
.
Источник тока, включенный между узлами
3 и 2, дает ток ![]() .
.
Решение. Записываем систему уравнений:
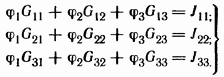
Подсчитываем проводимости:

При
подсчете ![]() учтено,
что проводимость ветви с источником
тока равна нулю (сопротивление источника
тока равно бесконечности).
учтено,
что проводимость ветви с источником
тока равна нулю (сопротивление источника
тока равно бесконечности).
Узловые токи:
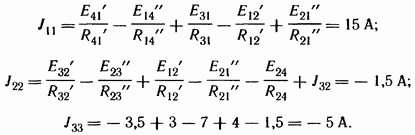
Система уравнений
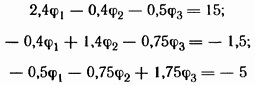
имеет
решение ![]() .
.
Заключительный этап расчета состоит в подсчете токов по закону Ома. Перед определением токов в ветвях схемы следует эти токи обозначить и выбрать для них положительные направления:
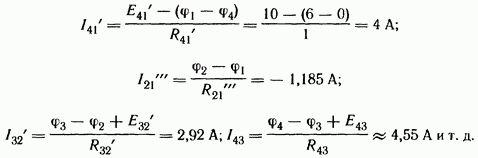
Сделаем проверку решения по второму закону Кирхгофа для периферийного контура.
Алгебраическая
сумма падений напряжений ![]() .
.
Алгебраическая
сумма ЭДС ![]() .
.
Покажем,
что основная формула (2.20) метода двух
узлов получается как частный случай
(2.22). Действительно, если один узел схемы
(рис. 2.23), например узел 6, заземлить, то
остается найти только один потенциал ![]() Для
получения формулы (2.20) из (2.22) следует
положить
Для
получения формулы (2.20) из (2.22) следует
положить ![]()
Метод двух узлов.
Часто встречаются схемы, содержащие всего два узла; на рис. 2.23 изображена одна из таких схем. Наиболее рациональным методом расчета токов в них является метод двух узлов.
Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое (с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы.
Расчетные формулы этого метода получают на основе формул (2.16а) и (2.16); их также можно просто получить из более общего метода — метода узловых потенциалов (см. § 2.22).
В
отличие от схемы рис. 2.21, а ток ![]() к
узлам
к
узлам ![]() схемы
рис. 2.23 не подтекает. Поэтому если в
формуле (2.16а) принять
схемы
рис. 2.23 не подтекает. Поэтому если в
формуле (2.16а) принять ![]() то
из нее может быть найдено напряжение
между двумя узлами:
то
из нее может быть найдено напряжение
между двумя узлами:
![]()
После
определения напряжения ![]() находят
ток в любой
находят
ток в любой ![]() ветви
по формуле
ветви
по формуле ![]()
Пример
22. Найти токи в схеме рис. 2.23, и сделать
проверку баланса мощности, если ![]()
Решение. Определим токи в схеме рис. 2.23:
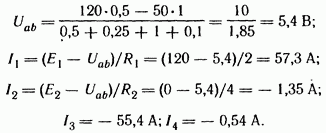
В
схеме потребляется мощность ![]()
![]()
Источники
ЭДС доставляют мощность ![]()