Точку называют полюсом n-го порядка для функции . При полюс называют простым.

Для того чтобы точка была полюсом n-го порядка функции , необходимо и достаточно, чтобы функцию можно было представить в виде , где аналитична в точке и

Теорема 2.

Для того чтобы точка была полюсом n-го порядка функции , необходимо и достаточно, чтобы главная часть ряда Лорана функции в точке имела конечное число членов, не более , причём , то есть

3. 
   Существенно особая точка
   

Опред. Изолированная особая точка называется существенно особой точкой, если не существует.

Теорема 3

Для того чтобы точка была полюсом n-го порядка функции , необходимо и достаточно, чтобы главная часть ряда Лорана функции в точке содержала бесконечно много членов.

Замечание.

Исследование характера бесконечно удалённой точки удобно проводить заменой

---

при этом

18. Вычет аналитической функции в изолированной особой точке.

19. Поведение аналитической функции в окрестности бесконечно удалённой точки. Вычет аналитической функции в бесконечно удалённой точке.

Вычет в бесконечно удалённой точке

Функция аналитична в бесконечно удалённой точке 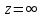, если функция 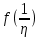аналитична в точке 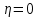. Например, функция 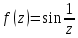аналитична в точке 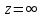, так как функция 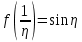аналитична в точке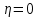

Опред. Бесконечно удалённая точка 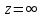комплексной плоскости называется изолированной особой точкой однозначной аналитической функции , если можно указать такое , что вне круга 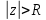функция не имеет особых точек, находящихся на конечном расстоянии от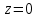



Возможны следующие случаи:

1. 
   Точка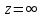 называется странимой особой точкой функции , если ряд Лорана не содержит членов с положительными степенями , то есть 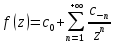, или существует конечный предел 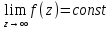, не зависящий от способа предельного перехода.
   

---

Если 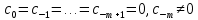, то является нулём порядка .

2. 
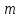   Точка называется полюсом m-го порядка функции , если ряд Лорана содержит конечноге число 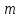членов с положительными степенями , то есть 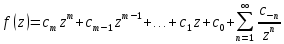, или эта функция неограниченно возрастает по модулю при 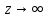независимо от предельного перехода.
   
3. 
   Точка называется существенно особой точкой функции , если ряд Лорана содержит бесконечное число членов с положительными степенями , то есть 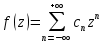, или в зависимости от выбора последовательности 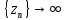можно получить 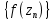, сходящуюся к любому наперед заданному пределу.
   

Опред.

Вычетом аналитической функции в точке называется комплексное число 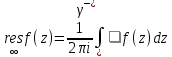, где 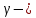произвольный замкнутый контур, проходимый по часовой стрелке(так что окрестность точки остаётся слева), вне которого функция является аналитической и не имеет особых точек, отличных от

---

.

Отсюда следует что

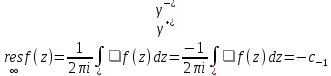
Замечание.

Вычет аналитической функции относительно бесконечно удалённой устранимой особой точки, в отличие от конечной особой устранимой точки, может оказаться отличным от нуля.

20. Основные теоремы теории вычетов.

21. Вычисление интегралов вида ∫????(si????????,co????????)????????2????0.

Интеграл 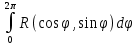, где 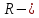рациональная функция

Сводится к контурным интегралам с помощью замены: 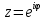. Очевидно, что 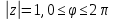и точка один раз опишет окружность против часовой стрелки. Тогда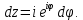

Отсюда .

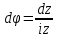Имеем





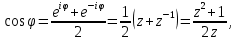
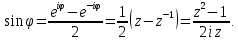
22. Вычисление интегралов вида ∫????(????)????????+∞−∞.

23. Вычисление интегралов вида ∫????????????????????(????)????????+∞−∞. Лемма Жордана.

Интеграл вида

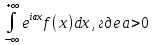
Лема 2 (Жордана).

Пусть функция является аналитической в верхней полуплоскости 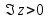, за исключением конечного числа изолированных особых точек, и равномерно относительно 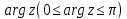стремится к нулю при 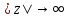. Тогда при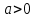



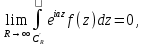
Где 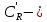дуга полуокружности

---

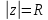в верхней полуплоскости.

Теорема 2.

Пусть функция , заданная на действительной оси 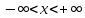, может быть аналитическое продолжение в верхней полуплоскости удовлетворяет условиям леммы Жордана и не имеет особых точек на действительной оси. Тогда при существует несобственный интеграл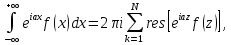



Где 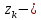особые точки функции в верхней полуплоскости.

Замечание 1

Если 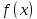чётная функция, то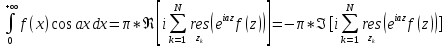



Замечание 2

Если 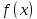нечётная функция, то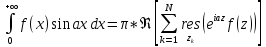



24. Преобразование Лапласа, его свойства. Таблица оригиналов и изображений.

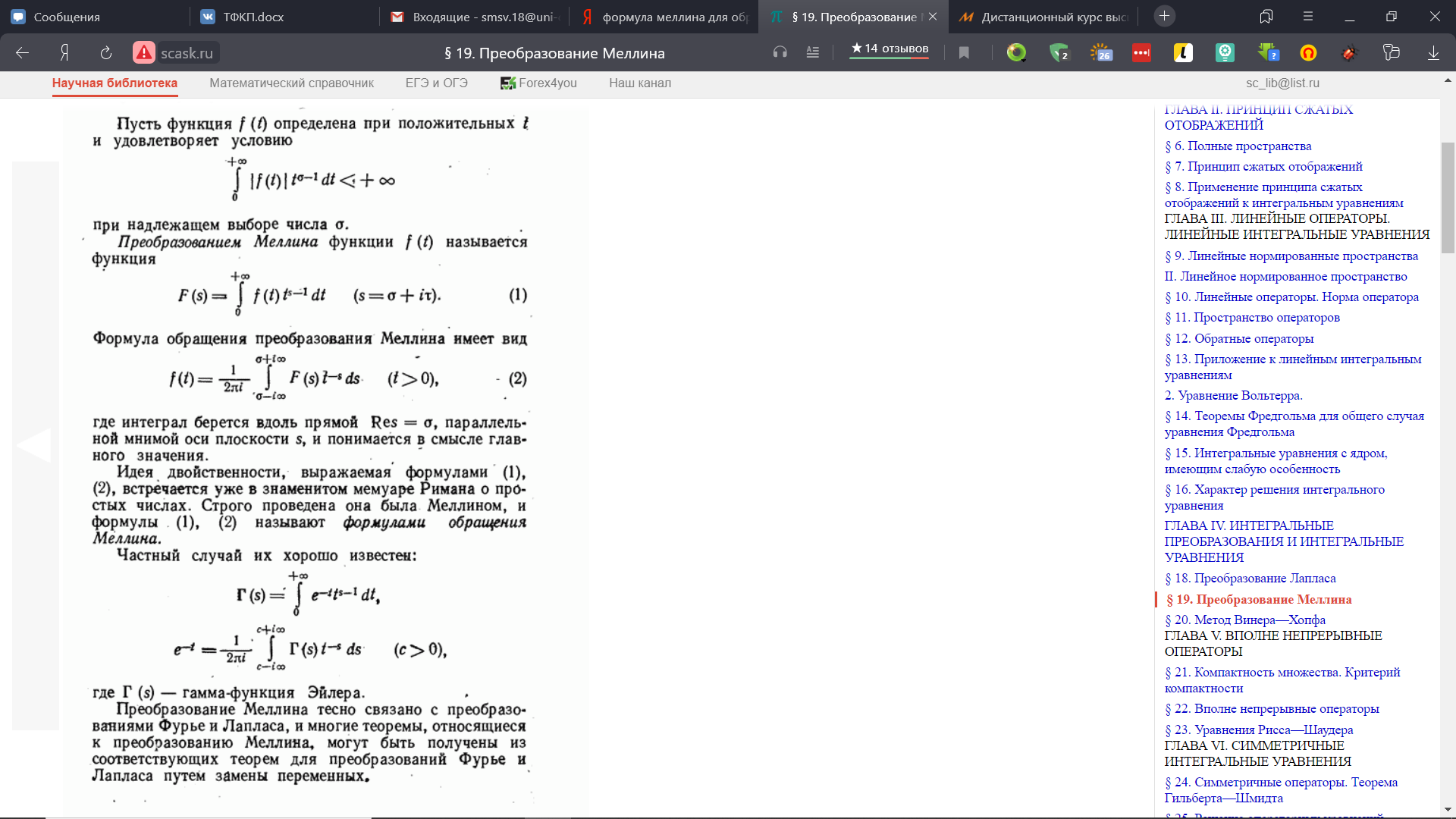
25. Нахождение оригинала по его изображению. Формула Меллина. Теоремы обращения.



https://studizba.com/lectures/47-matematika/679-ryady-fure-i-teoriya-funkciy-kompleksnoy-peremennoy/13015-17-teoremy-razlozheniya.html

26. Применение преобразования Лапласа к решению дифференциальных уравнений.

---

Смотрите также файлы

• Характеристика торгового предприятия.doc

• Брак и семья.doc

• Итоговая работа по обж за курс 9 класса. Рекомендованное время выполнения 15 минут.docx

• 3. Experience is the best teacher. Let me share my opinion about the statement Experience is the best teacher.docx

• Вопросник по вт.docx