Министерство науки и высшего образования Российской Федерациифедеральное государственное автономное образовательное учреждение высшего образования«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИТМО»Отчет по лабораторной работе №7 «Анализ точности систем управления» по дисциплине «Теория автоматического управления» Авторы: Есаулов ЛевТитова ЕкатеринаФакультет: СУиР Группа: R33812Преподаватель: Чепинский С.АВариант: 10Санкт-Петербург, 2023Цель работы. Исследование точностных свойств систем управления.Порядок выполнения работы.

1. 
   Исследуем систему с астатизмом нулевого порядка
   

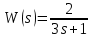
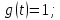
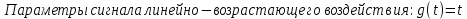
Исходные данные:Передаточная функция: Параметры постоянного сигнала воздействия: Общий коэффициент усиления разомкнутой системы:

1. 
   Исследование стационарного режима работы: .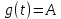
   

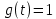
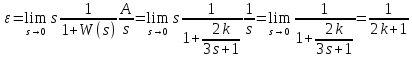
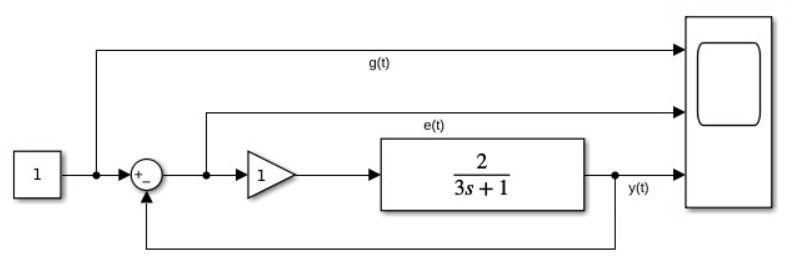
Моделируем замкнутую систему и получаем переходные процессы для трех различных значений коэффициента k и определяем предельное значение установившейся ошибки :Рис 1.1. Схема моделирования системы с астатизмом нулевого порядка в стационарном режиме работы При k = 1:

---

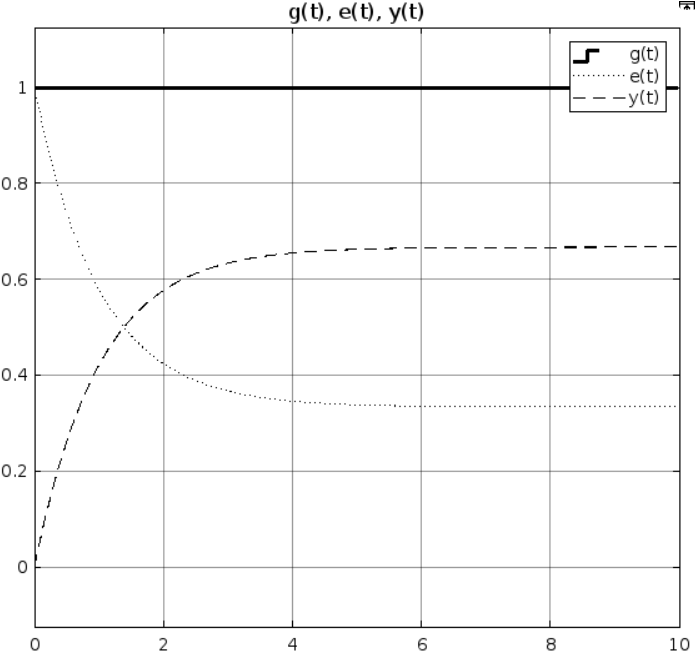
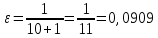
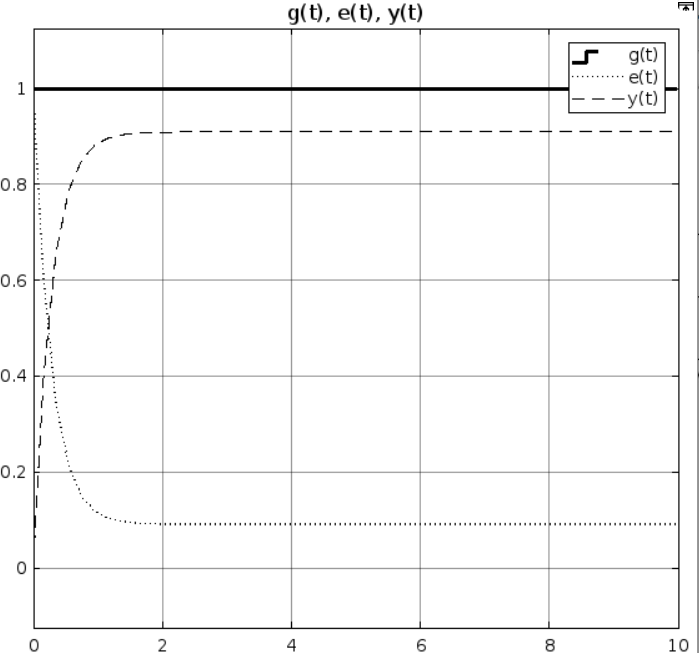
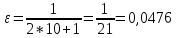
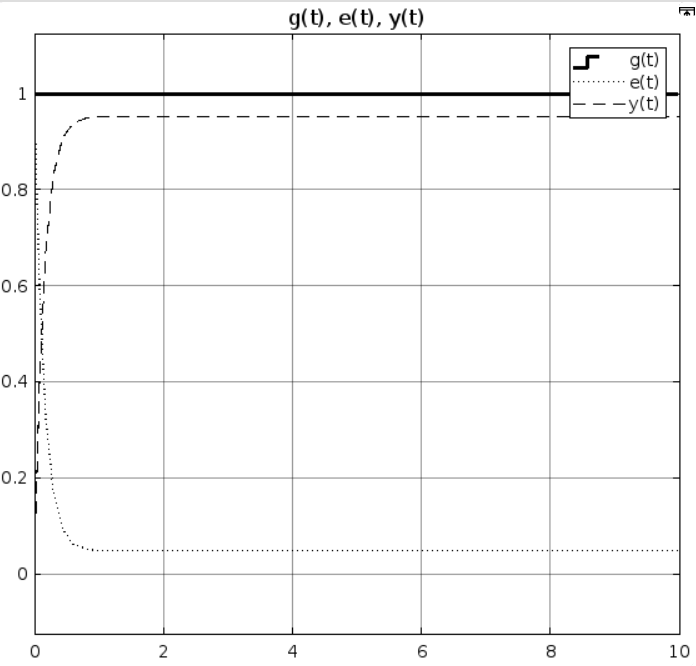
Рис 1.2 Результат моделирования при k = 1 При k = 5: Рис 1.3 Результат моделирования при k = 5При k = 10: Рис 1.4 Результат моделирования при k = 10

2. 
   Исследование режима движения с постоянной скоростью: .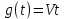
   

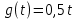
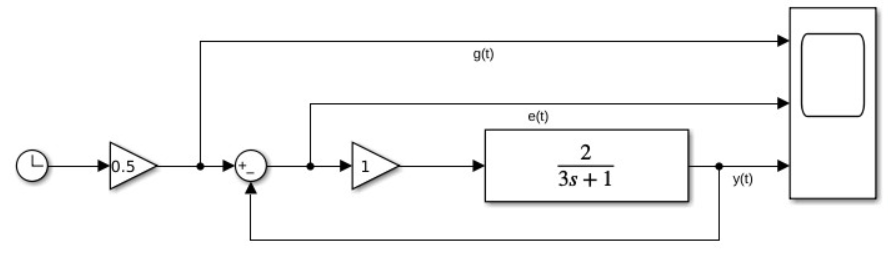
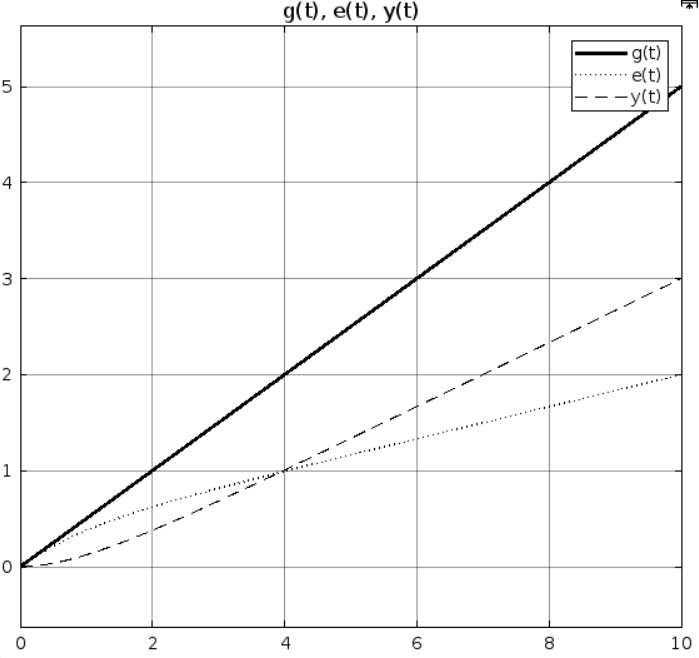
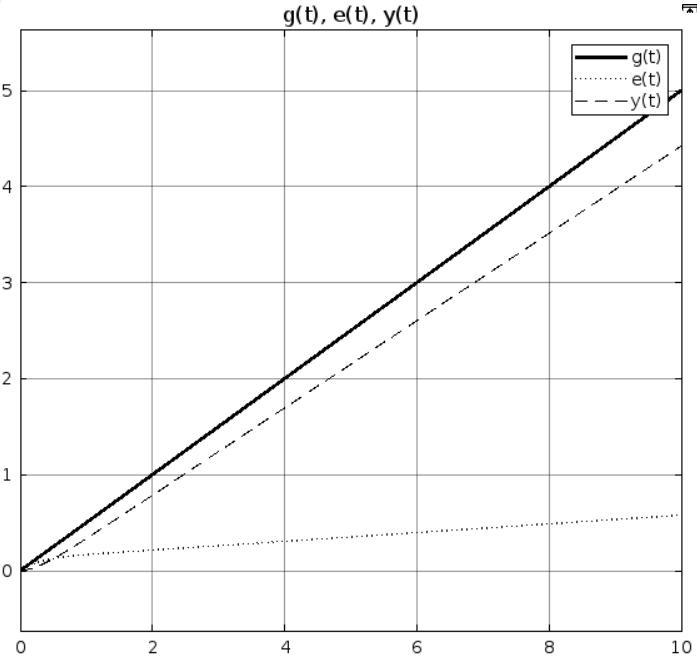
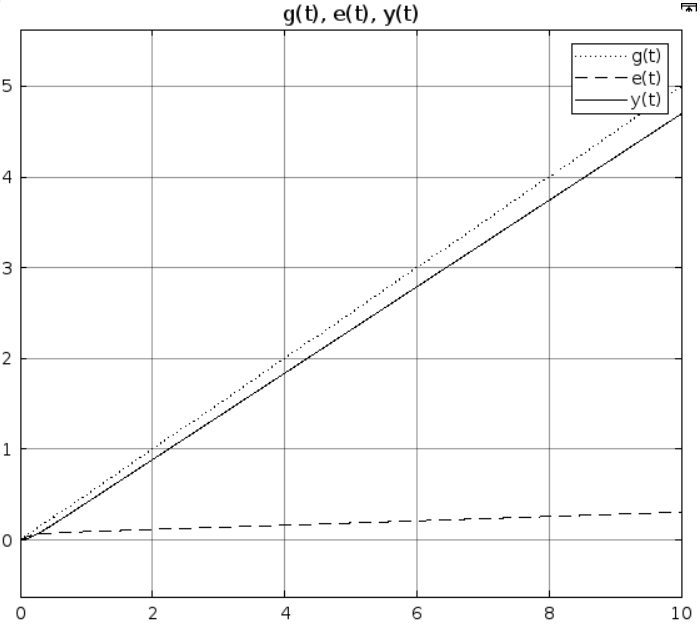
Моделируем замкнутую систему и получаем переходные процессы для трех различных значений коэффициента k:Рис 1.5. Схема моделирования системы с астатизмом нулевого порядка с режимом движения с постоянной скоростьюРис 1.6. Результат моделирования при k = 1Рис 1.7. Результат моделирования при k = 5Рис 1.8. Результат моделирования при k = 10

2. 
   Исследование системы с астатизмом первого порядка
   

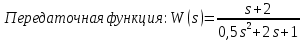
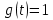
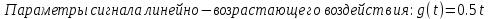
Исходные данные: Параметры постоянного сигнала воздействия: Характеристики квадратично нарастающего задающего воздействия:

1. 
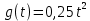
   Исследование стационарного режима работы: .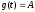
   

---

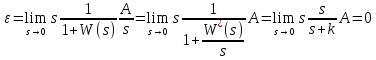
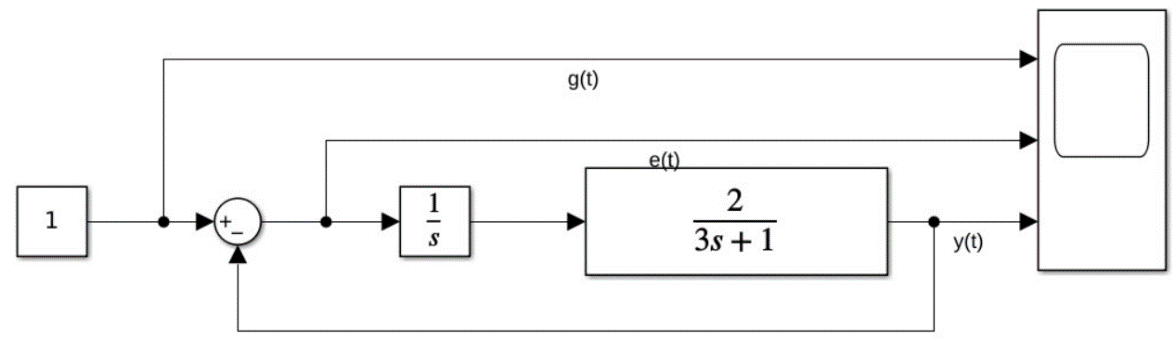
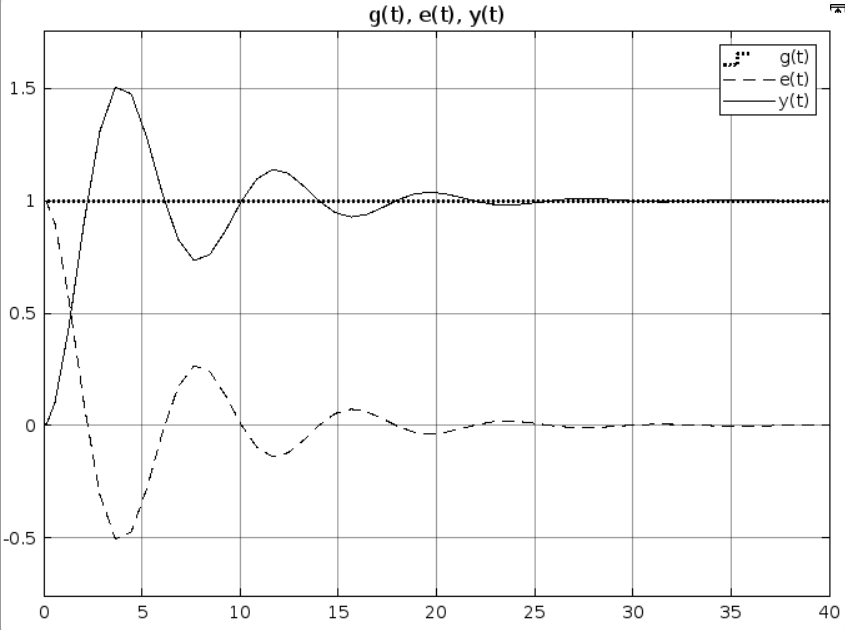
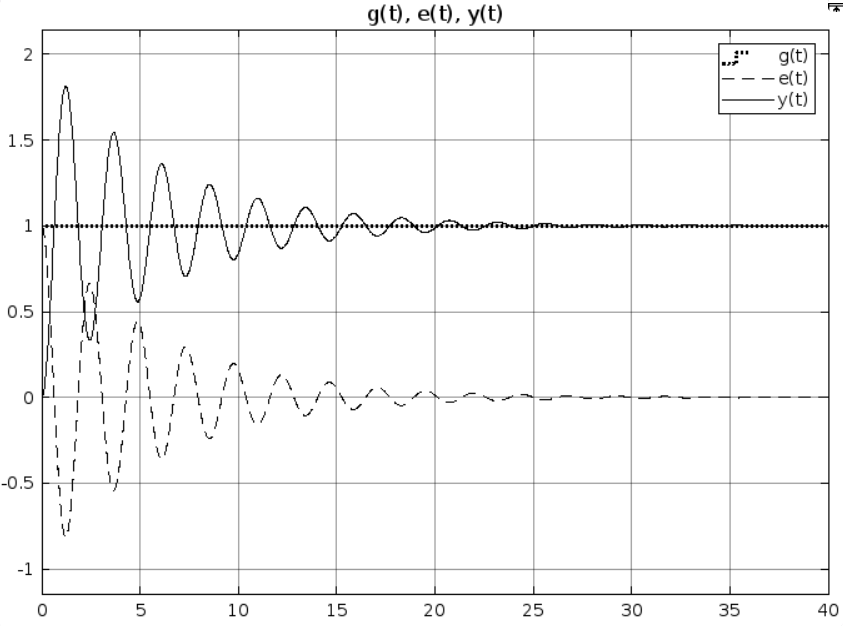
Получаем переходные процессы для различных значений коэффициента и Определяем предельное значение установившейся ошибки :Рисунок 2.1 Схема моделирования системы с астатизмом первого порядка в стационарном режиме работыРис 2.2. Результат моделирования при k = 1Рис 2.3. Результат моделирования при k = 5Рис 2.4. Результат моделирования при k = 10

2. 
   Исследование режима движения с постоянной скоростью: .
   

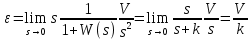
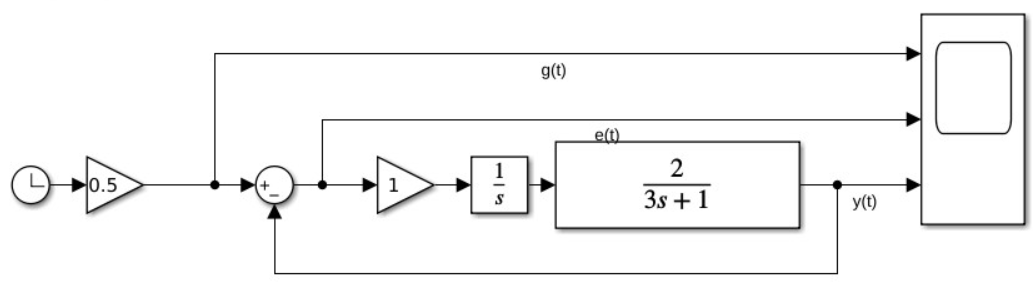
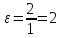
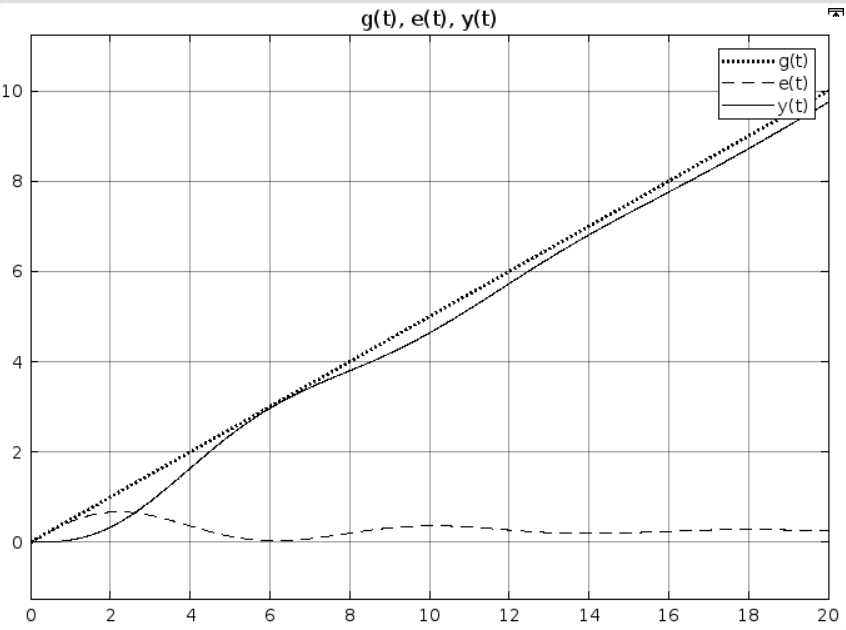
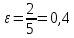
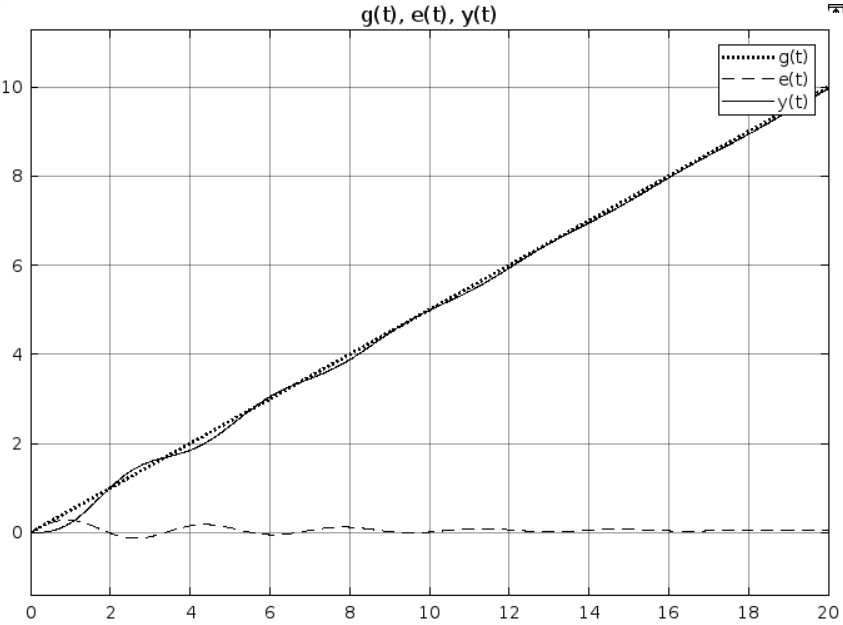
Определяем предельное значение установившейся ошибки для различных значений коэффициента :Рис 2.5. Схема моделирования системы с астатизмом первого порядка с режимом движения с постоянной скоростьюПри k = 1: Рис 2.6. Результат моделирования при k = 1При k = 5: Рис 2.7. Результат моделирования при k = 5 При k = 10:

---

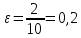
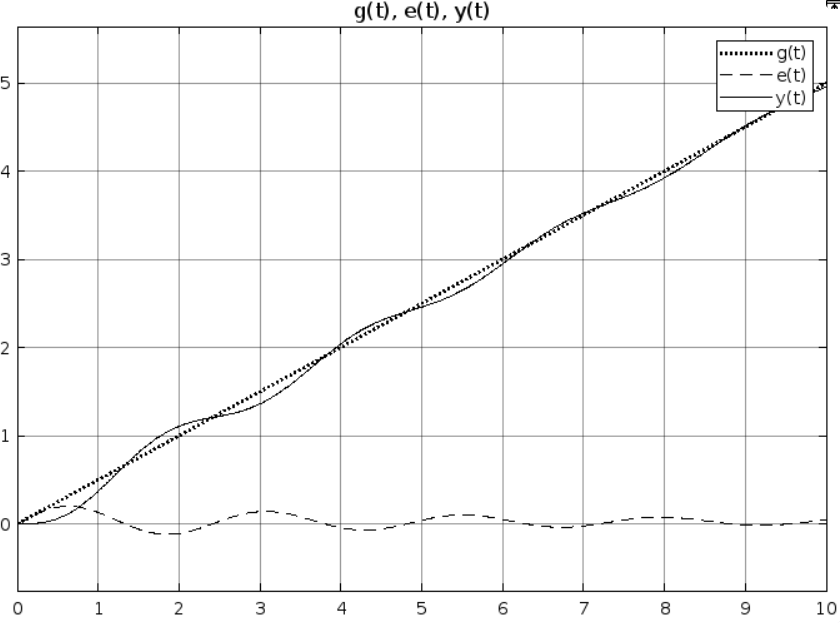
Рис 2.8. Результат моделирования при k = 10

3. 
   Исследование режима движения с постоянным ускорением :
   

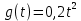
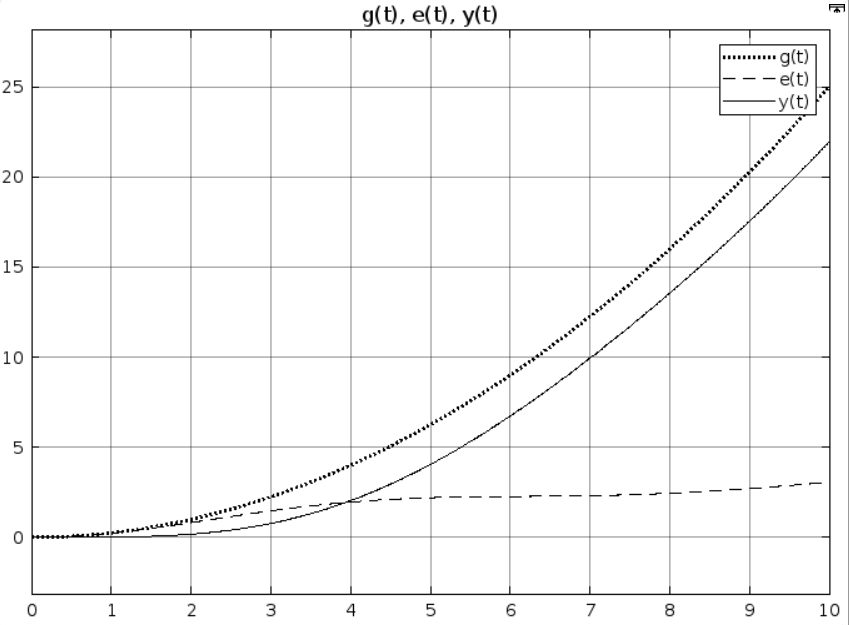
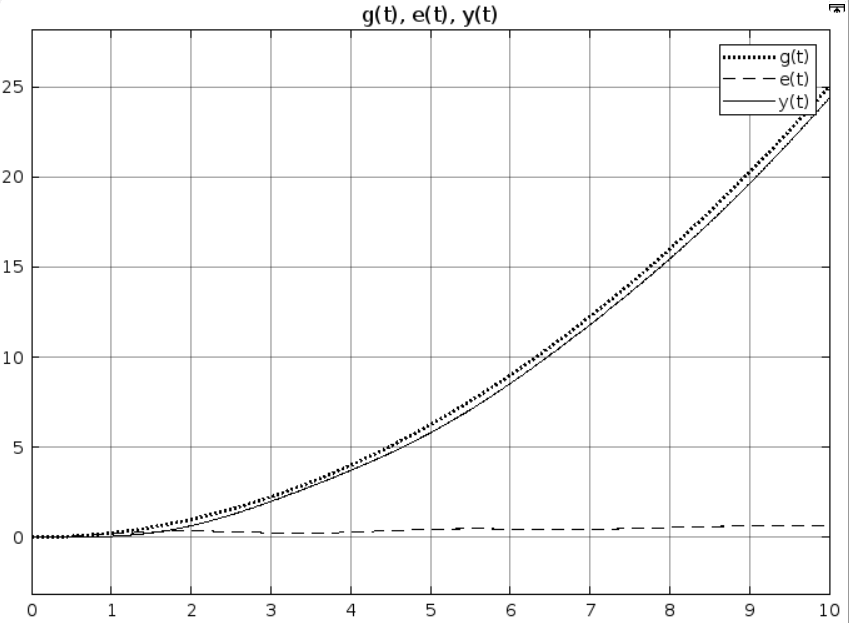
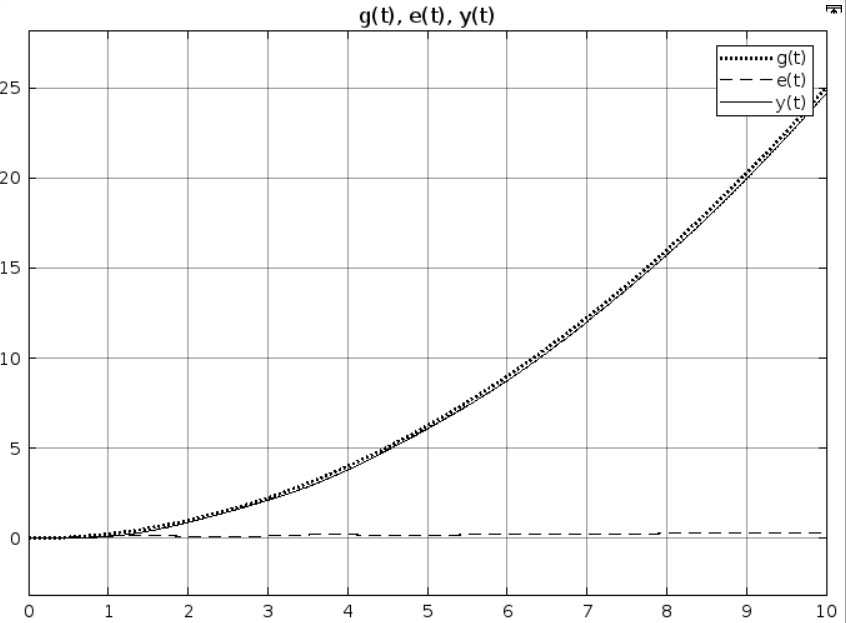
Рис 2.9. Схема моделирования системы с астатизмом первого порядка с режимом движения с постоянным ускорениемРис 2.10. Результат моделирования при k = 1Рис 2.11. Результат моделирования при k = 5Рис 2.12. Результат моделирования при k = 10

3. 
   Исследование влияния внешних возмущений.
   

Исходные данные: Передаточная функция: :

1. 
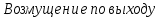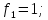
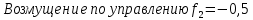
   В соответствии с вариантом задания собираем схему моделирования
   

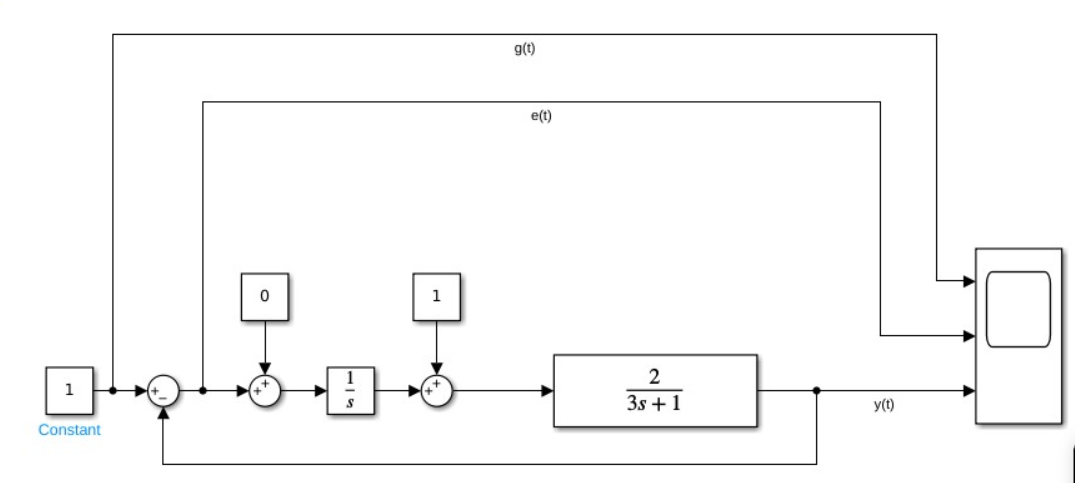
Рис 3.1. Схема моделирования возмущенной системы

2. 
   Определим предельное значение установившейся ошибки при
   

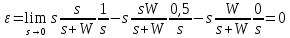
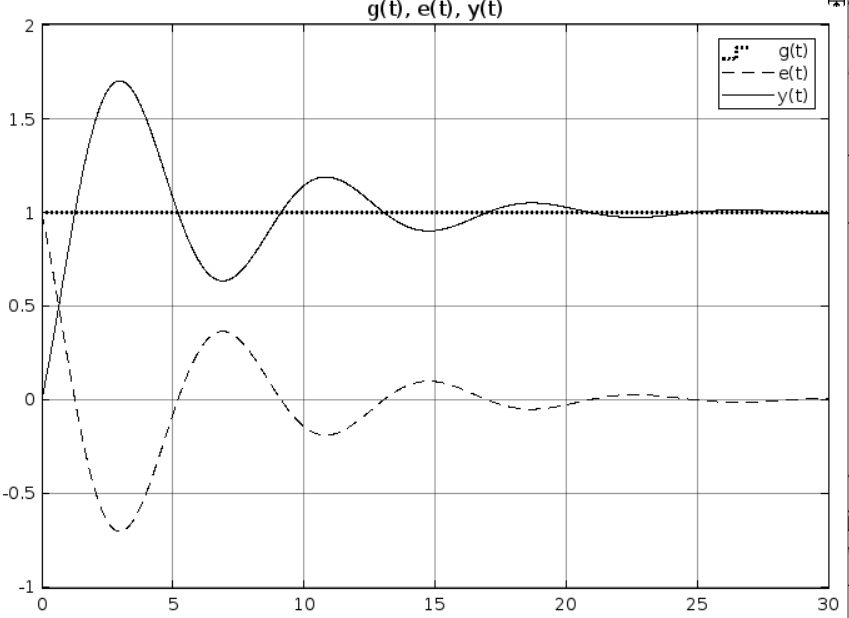
f₁(t) = 1;f₂(t) = 0;g(t) = 1;Рис 3.2. Результаты моделирования

3. 
   Определим предельное значение установившейся ошибки при
   

---

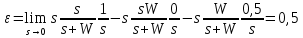
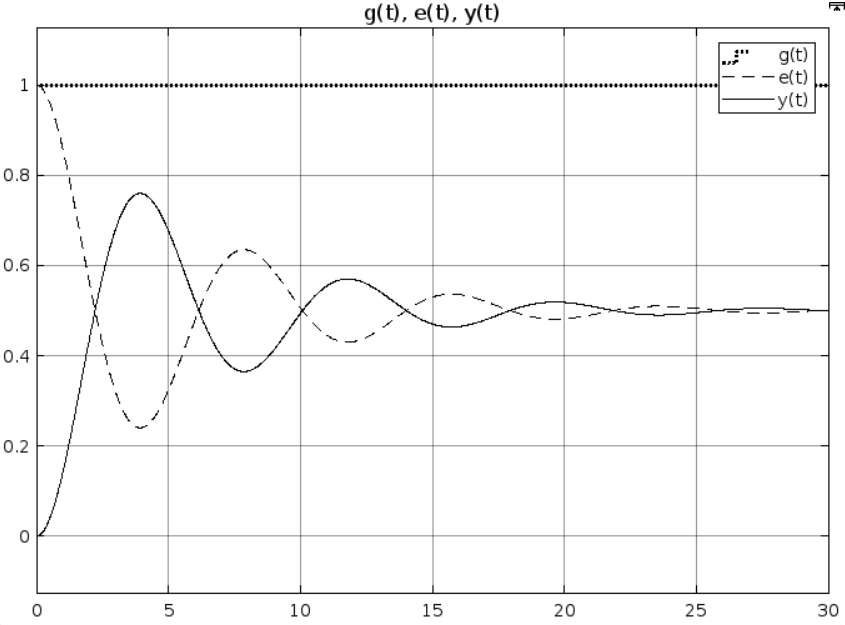
f₁(t) = 0;f₂(t) = 0.5;g(t) = 1;Рис 3.3. Результаты моделирования

4. 
   Исследование установившейся ошибки при произвольном входном воздействии.
   

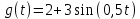
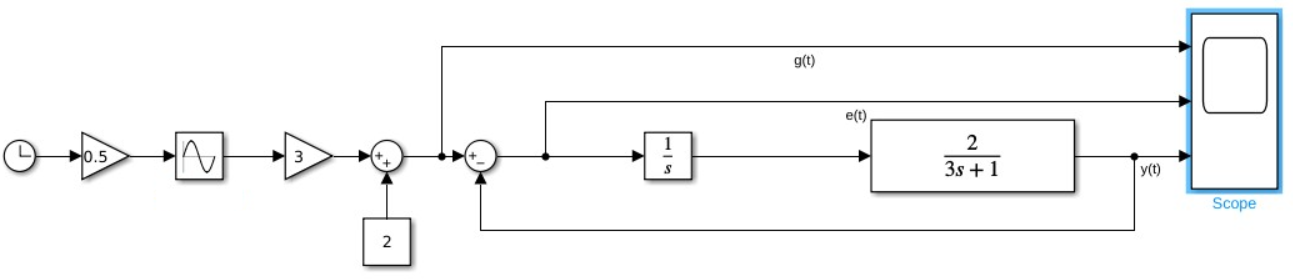
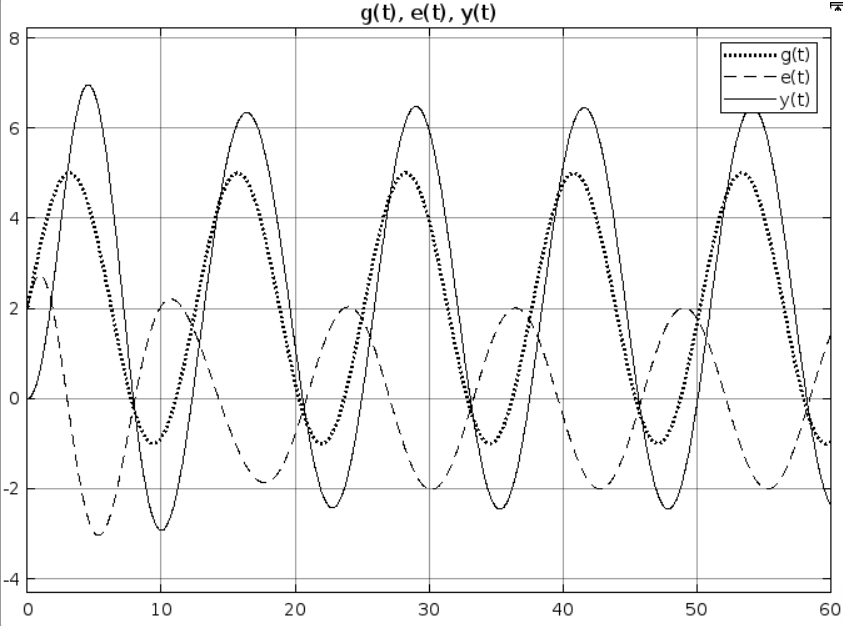
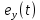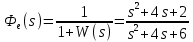
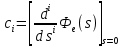
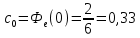
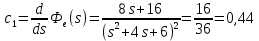
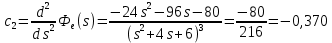
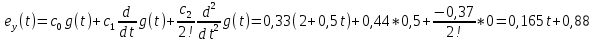
Задающее воздействие: Передаточная функция: Моделируем замкнутую систему с регулятором :Рис 4.1. Схема моделирования системыРис 4.2 Результаты моделированияПолучаем приближенное аналитическое выражение для , сохранив в ряде Тейлора три первых члена:Вывод: По графикам моделирования системы с астатизмом нулевого порядка мы можем увидеть, что значение установившейся ошибки уменьшается с увеличением коэффициента k регулятора в стационарном режиме работы. В режиме движения с постоянной скоростью график ошибки при более высоких значениях коэффициента k регулятора лежит ближе к нулевой оси. По графикам моделирования системы с астатизмом первого порядка мы видим, что значение установившейся ошибки равно 0 при любых значениях коэффициента k регулятора в стационарном режиме работы. В режиме движения с постоянной скоростью значение установившейся ошибки всегда равно V/k. В режиме движения с постоянным ускорением график ошибки при более высоких значениях коэффициента k регулятора лежит ближе к нулевой оси. По графикам моделирования возмущённой системы видно, что при отсутствии возмущения f

---

Смотрите также файлы

• Инструкция бухгалтера общие положения.docx

• Обучение физике на основании требований обновленных фгос ооо, фгос соо.odt

• Понятие и сущность общей физической подготовки, и её значение для гармонического развития.docx

• Чусовлянкина Евгения Юрьевича На тему Развитие пешеходного туризма в России (на примере турбазы Малиновка) Состав дипломной работы 1 пояснительная записка.doc

• Мошенничество Телефонные мошенничестваКак распознать мошенника.pdf