Векторлық шамаларды геометриялық тұрғыдан алғанда бағытталған кесінді арқылы бейнелейді.

Берілген екі нүкте түзудің кесіндісін анықтайды. Бұл нүктелердің бірін кесіндінің басы деп, ал екіншісін кесіндінің ұшы деп атайды. Сөйтіп, жазықтықта немесе кеңістікте реттеліп алынған екі нүкте арқылы бағытталған кесінді пайда болады.

Анықтама. Жазықтықтағы немесе кеңістіктегі бағытталған кесіндіні вектор деп, ал басы мен ұшы беттесетін векторды нольдік вектор деп атайды.

Жазу барысында векторды белгілейтін әріптердің үстіне сызықша қояды: мысалы . Векторды бұлaй жазғанда вектордың басы болатын нүкте міндетті түрде алдымен жазылады, ал оның ұшының белгілеуі екінші орында тұрады. Вектордың басы мен ұшы тиянақты болмаған жағдайда векторды белгілеу үшін үстіне сызықша қойылған бір әріпті де қолданады: т. б.

Нольдік векторды арқылы белгілейді.

Анықтама. Вектордың басы мен ұшының ара қашықтығы оның ұзындығы деп аталады. Ұзындықты кейде модуль деп те атайды.Вектордың ұзындығын немесе таңбалары арқылы белгілейді, оқығанда немесе векторының ұзындығы.

Нольдік-вектордың ұзындығы нөльге тең:



Анықтама. Егер екі вектор бір түзуде жатса немесе параллель болса, онда мұндай векторларды коллинеар деп атайды.

және

---

коллинеар векторлар деп жазылады

Нольдік вектор кез-келген векторға коллинеар болады. Өйткені нольдік вектордың тиянақты бір бағыты жоқ. Анықтама бойынша қандай да болмасын вектор өзіне-өзі коллинеар болатындығы түсінікті.

Анықтама. Егер мен векторлары коллинеар, бірдей бағытталған және олардың ұзындықтары тең болса, онда мүндай векторларды тең деп атайды.

Басқаша айтқанда және болса, онда және векторлары тең болады, яғни = . [5]

Сонымен екі вектордың теңдігін айқындау үшін осы анықтамадағы үш шарттың (коллинеарлығы; бірдей бағытталғандығы және ұзындықтарының теңдігі) орындалуын тексеру керек. Егер бұл шарттардың, ең болмағанда біреуі орындалмаса, онда векторлардың өзара тең болмағандығы.

Векторлар теңдігінің анықтамасына сүйене отырып және кезкелген нүктесін сайлап алып, берілген векторына тең болатын векторын салуға болады (Тең векторлар сурет – 1), мұндағы

---

- параллелограмм. теңдігі параллелограмм қасиеттерінен келіп шығады.



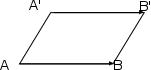
Тең векторлар сурет – 1
Векторды санға көбейту. Векторларға қолданылатын амалдардың бірі - векторын санына көбейту. Бұл ұғымға анықтама бермес бұрын нақты санының абсолют шамасын анықтап алалық: нақты санының абсолют шамасы (модулі) былай анықталады:

Анықтама. векторының нөлден өзге санына көбейтіндісі дегеніміз мынандай шарттарды қанағаттандыратын векторын айтады:

біріншіден, векторы векторына коллинеар;

екіншіден, -нің модулі мен -ның модулдерінің көбейтіндісіне тең, яғни


үшіншіден, егер

---

болса, мен векторлары бірдей бағытталған, ал болса, онда бұл векторлар қарама-қарсы бағытталған.

Векторды санға көбейтудің мынадай қасиеті бар:

Кез-келген α, β сандары және кез-келген векторы үшін (1.1) тендігі орындалады. Шынында да, (1.1) теңдіктің екі жағында тұрған векторлардың ұзындықтары бірдей, ол көбейтіндісіне тең. Осы айтылып отырған векторлардың бағыттары да бірдей.

Егер мен - ның таңбалары бірдей болса, онда -ның бағытындай, ал мен ның таңбалары қарама-қарсы болса, сол екі вектордың бағыты -ның бағытымен қарама-қарсы. Егер мен және -ның ең болмағанда береуі нөльге тең болса, онда теңдіктің екі жағында нөл тұрады.

---

Сонымен (1.1) теңдік толық дәлелденді. Теорема. және векторлары коллинеар болу үшін (1.2)

теңдігі орындалатындай санының табылуы қажетті және жеткілікті. [6]

Дәлелі: Қажеттілігі. а) үшін орындалатын саны болатынын дәлелдейік.

1. 
   Егер болса, онда үшін
   
2. 
   болсын: егер болса, онда үшін , себебі және
   

б) егер болса, онда үшін теңдігін аламыз

Жеткіліктілігі: Егер

---

Смотрите также файлы

• Тема Особенности содержания обновленных фгосооо, фгос соо.docx

• Вопросы к дифференцированному зачету.docx

• Современное использование.docx

• Отчет по производственной практике практики по получению профессиональных умений и опыта профессиональной деятельности.docx

• Практическое задание Развитие талантов каждого олимпиадное движение, конкурсы, фестивали.docx