ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(3.21)
Соответственно дифференциалы потенциалов (3.21) имеют вид:
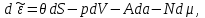 (3.22а)
(3.22а)
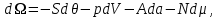 (3.22б)
(3.22б)
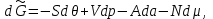 (3.22в)
(3.22в)
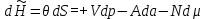 (3.22г)
(3.22г)
Также как и для термодинамических потенциалов первой группы, для потенциалов (3.21) можно построить термодинамические тождества, найти выражения параметров термодинамической системы и т.д.
Рассмотрим характерные соотношения для “потенциала омега”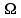 , выражающий квазисвободную энергию, и использующийся на практике наиболее часто среди остальных потенциалов группы (3.22).
, выражающий квазисвободную энергию, и использующийся на практике наиболее часто среди остальных потенциалов группы (3.22).
Потенциал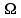 задается в переменных (
задается в переменных (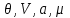 ), описывающих термодинамическую систему с воображаемыми стенками. Параметры системы в этом случае определяются из соотношений:
), описывающих термодинамическую систему с воображаемыми стенками. Параметры системы в этом случае определяются из соотношений:
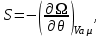

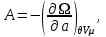
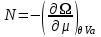 (3.23)
(3.23)
Термодинамические тождества, следующие из потенциальности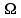 , имеют вид:
, имеют вид:
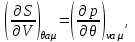
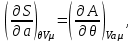
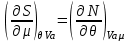
(3.24)
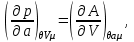
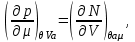
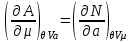
Достаточно интересными являются аддитивные свойства термодинамических потенциалов второй группы. Поскольку в этом случае число частиц не входит в число параметров системы, то в качестве аддитивного параметра используют объем. Тогда для потенциала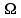 получаем:
получаем:
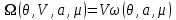 (3.25)
(3.25)
Здесь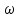 - удельный потенциал
- удельный потенциал 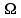 на 1
на 1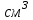 . Учитывая (3.23), получаем:
. Учитывая (3.23), получаем:
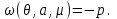 , соответственно,
, соответственно, 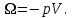 (3.26)
(3.26)
Справедливость (3.26) можно доказать и на основе (3.15):
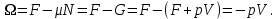
Потенциал также может быть использован для пересчета термодинамических функций, записанных в виде
также может быть использован для пересчета термодинамических функций, записанных в виде 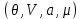 к виду
к виду 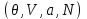 . Для этого соотношение (3.23) для N:
. Для этого соотношение (3.23) для N:
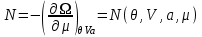
разрешается относительно :
: 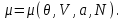
В качестве термодинамических потенциалов могут выступать не только энергетические характеристики системы, но и любые другие величины, входящие в соотношение (3.1). В качестве важного примера рассмотрим энтропию как термодинамический потенциал. Исходное дифференциальное соотношение для энтропии следует из обобщенной записи I и II начал термодинамики:
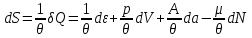 (3.27)
(3.27)
Таким образом, энтропия является термодинамическим потенциалом для системы, заданной параметрами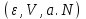 . Другие параметры системы имеют вид:
. Другие параметры системы имеют вид:

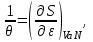

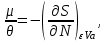
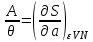 (3.28)
(3.28)
Разрешая первое из соотношений (3.28) относительно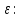
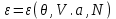 возможен переход от переменных
возможен переход от переменных 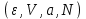 к переменным
к переменным 
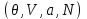 .
.
Аддитивные свойства энтропии приводят к известным соотношениям:
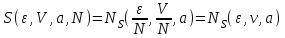 (3.29)
(3.29)
Перейдем к определению термодинамических потенциалов на основе заданных макроскопических состояний термодинамической системы. Положим для упрощения вычислений отсутствие внешних полей (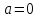
). Это не снижает общности результатов, поскольку при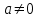 в результирующих выражениях просто появляются дополнительные системы.
в результирующих выражениях просто появляются дополнительные системы.
В качестве примера найдем выражения свободной энергии, используя в качестве исходных уравнение состояния, калорическое уравнение состояния и особенности поведения системы при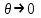 . Учитывая (3.3) и (3.12), находим:
. Учитывая (3.3) и (3.12), находим:
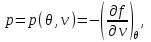
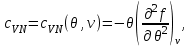
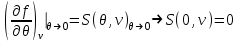 (3.30)
(3.30)
Проинтегрируем второе уравнение системы (3.30) с учетом граничного условия при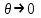 :
:
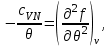
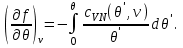
Тогда система (3.30) принимает вид:
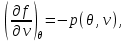
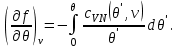 (3.31)
(3.31)
Решение системы (3.31) позволяет найти удельную свободную энергию в виде
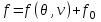 (3.32)
(3.32)
Начало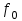 отсчета удельной свободной энергии также может быть найдено из условий при
отсчета удельной свободной энергии также может быть найдено из условий при 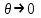 :
:
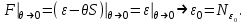
Тогда (3.32) принимает вид:
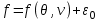 , (3.33а)
, (3.33а)
а выражение всей свободной энергии системы с точностью до аддитивной постоянной принимает вид:
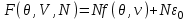 (3.34)
(3.34)
Тогда реакция системы на включение внешнего поля задается дополнительным уравнением состояния, которое в зависимости от набора переменных состояния имеет вид:
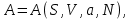 или
или 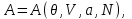
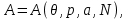
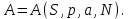 (3.35)
(3.35)
Тогда изменение соответствующего термодинамического потенциала, связанное с включением нуля от нуля до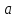 , определяется из выражений :
, определяется из выражений :

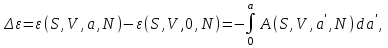
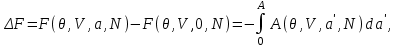 (3.36)
(3.36)
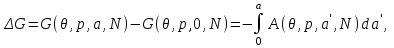
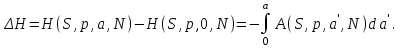
Таким образом, задание термодинамического потенциала в макроскопической теории возможно только на основе использования заданных уравнений термодинамического состояния, которые в свою очередь, сами получаются на основе задания термодинамических потенциалов. Разорвать этот “замкнутый круг” можно только на основе микроскопической теории, в которой состояние системы задается на основе функций распределения с учетом статистических особенностей.
3.
Обобщим полученные результаты на случай многокомпонентных систем. Это обобщение осуществляется путем замены параметра множеством
множеством 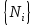 . Рассмотрим сказанное на конкретных примерах.
. Рассмотрим сказанное на конкретных примерах.
Положим, что термодинамическое состояние системы задано параметрами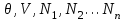 , т.е. мы рассматриваем систему в термостате, состоящую из нескольких компонентов, число частиц в которых равно
, т.е. мы рассматриваем систему в термостате, состоящую из нескольких компонентов, число частиц в которых равно 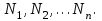 Свободная энергия, являющаяся в этом описании термодинамическим потенциалом, имеет вид:
Свободная энергия, являющаяся в этом описании термодинамическим потенциалом, имеет вид:
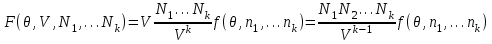 (3.37)
(3.37)
В качестве аддитивного параметра в (3.37) введены не число частиц, а объем системы V. Тогда через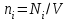 обозначена плотность системы. Функция
обозначена плотность системы. Функция 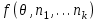 является неаддитивной функцией неаддитивных аргументов. Это достаточно удобно, поскольку при разбиении системы на части функция
является неаддитивной функцией неаддитивных аргументов. Это достаточно удобно, поскольку при разбиении системы на части функция 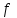 не изменится для каждой части.
не изменится для каждой части.
Тогда для параметров термодинамической системы можно записать:
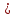
Учитывая, что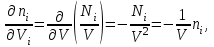 имеем
имеем
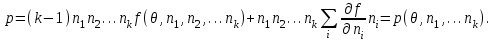 (3.38)
(3.38)
Для химического потенциала отдельного компонента запишем:
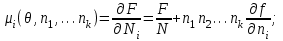 (3.39)
(3.39)
Существуют и другие способы учета аддитивных свойств свободной энергии. Введем относительные плотности чисел частиц каждой из компонент:
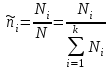 , (3.40)
, (3.40)
не зависящие от объема системы V. Здесь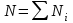 - общее число частиц в системе. Тогда
- общее число частиц в системе. Тогда
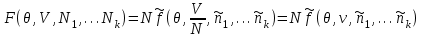 (3.41)
(3.41)
Выражение химического потенциала в этом случае принимает более сложный вид:
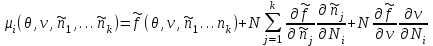
Вычислим производные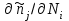 и
и 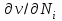 и подставим их в последнее выражение:
и подставим их в последнее выражение:

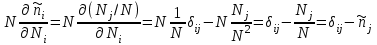
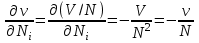
Тогда
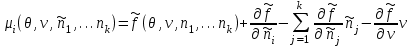 (3.42)
(3.42)
Выражение для давления, напротив упростится:
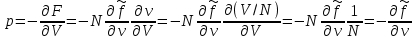 (3.43)
(3.43)
Аналогичные соотношения могут быть получены и для потенциала Гиббса. Так, если в качестве аддитивного параметра задан объем, то с учетом (3.37) и (3.38) запишем:
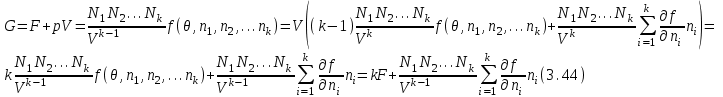 это же выражение может быть получено из (3.юю), которое в случае многих частиц принимает вид:
это же выражение может быть получено из (3.юю), которое в случае многих частиц принимает вид:
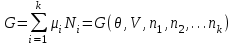 (3.45)
(3.45)
Подставляя в (3.45) выражение(3.39), находим:
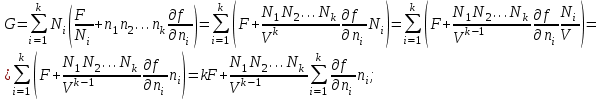
что полностью совпадает с (3.44).
Для того, чтобы перейти к традиционной записи потенциала Гиббса (через переменные состояния (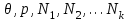 )) необходимо разрешить уравнение (3.38):
)) необходимо разрешить уравнение (3.38):
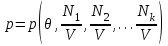
Относительно объема V и подставить результат в (3.44) или (3.45):
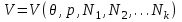
Если в качестве аддитивного параметра задано полное число частиц в системе N, то потенциал Гиббса с учетом (3.42) принимает следующий вид:

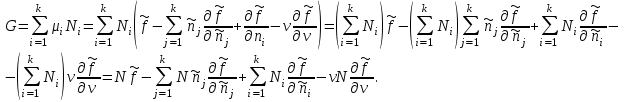
Зная вид удельных величин:
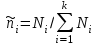 ,получим:
,получим:

Соответственно дифференциалы потенциалов (3.21) имеют вид:
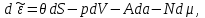 (3.22а)
(3.22а)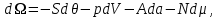 (3.22б)
(3.22б)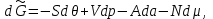 (3.22в)
(3.22в)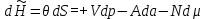 (3.22г)
(3.22г)Также как и для термодинамических потенциалов первой группы, для потенциалов (3.21) можно построить термодинамические тождества, найти выражения параметров термодинамической системы и т.д.
Рассмотрим характерные соотношения для “потенциала омега”
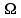 , выражающий квазисвободную энергию, и использующийся на практике наиболее часто среди остальных потенциалов группы (3.22).
, выражающий квазисвободную энергию, и использующийся на практике наиболее часто среди остальных потенциалов группы (3.22).Потенциал
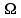 задается в переменных (
задается в переменных (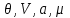 ), описывающих термодинамическую систему с воображаемыми стенками. Параметры системы в этом случае определяются из соотношений:
), описывающих термодинамическую систему с воображаемыми стенками. Параметры системы в этом случае определяются из соотношений: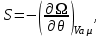
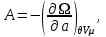
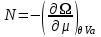 (3.23)
(3.23)Термодинамические тождества, следующие из потенциальности
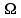 , имеют вид:
, имеют вид: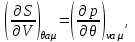
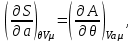
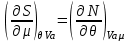
(3.24)
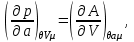
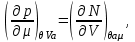
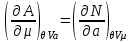
Достаточно интересными являются аддитивные свойства термодинамических потенциалов второй группы. Поскольку в этом случае число частиц не входит в число параметров системы, то в качестве аддитивного параметра используют объем. Тогда для потенциала
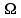 получаем:
получаем: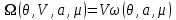 (3.25)
(3.25)Здесь
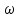 - удельный потенциал
- удельный потенциал 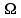 на 1
на 1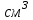 . Учитывая (3.23), получаем:
. Учитывая (3.23), получаем:
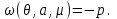 , соответственно,
, соответственно, 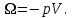 (3.26)
(3.26)Справедливость (3.26) можно доказать и на основе (3.15):
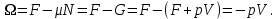
Потенциал
 также может быть использован для пересчета термодинамических функций, записанных в виде
также может быть использован для пересчета термодинамических функций, записанных в виде 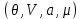 к виду
к виду 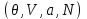 . Для этого соотношение (3.23) для N:
. Для этого соотношение (3.23) для N: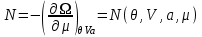
разрешается относительно
 :
: 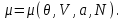
В качестве термодинамических потенциалов могут выступать не только энергетические характеристики системы, но и любые другие величины, входящие в соотношение (3.1). В качестве важного примера рассмотрим энтропию как термодинамический потенциал. Исходное дифференциальное соотношение для энтропии следует из обобщенной записи I и II начал термодинамики:
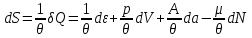 (3.27)
(3.27)Таким образом, энтропия является термодинамическим потенциалом для системы, заданной параметрами
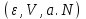 . Другие параметры системы имеют вид:
. Другие параметры системы имеют вид:
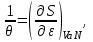

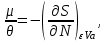
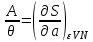 (3.28)
(3.28)Разрешая первое из соотношений (3.28) относительно
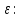
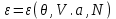 возможен переход от переменных
возможен переход от переменных 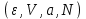 к переменным
к переменным 
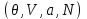 .
.Аддитивные свойства энтропии приводят к известным соотношениям:
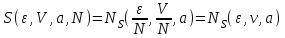 (3.29)
(3.29)Перейдем к определению термодинамических потенциалов на основе заданных макроскопических состояний термодинамической системы. Положим для упрощения вычислений отсутствие внешних полей (
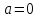
). Это не снижает общности результатов, поскольку при
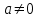 в результирующих выражениях просто появляются дополнительные системы.
в результирующих выражениях просто появляются дополнительные системы.В качестве примера найдем выражения свободной энергии, используя в качестве исходных уравнение состояния, калорическое уравнение состояния и особенности поведения системы при
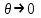 . Учитывая (3.3) и (3.12), находим:
. Учитывая (3.3) и (3.12), находим: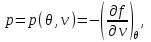
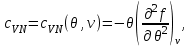
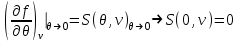 (3.30)
(3.30)Проинтегрируем второе уравнение системы (3.30) с учетом граничного условия при
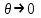 :
: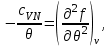
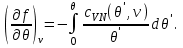
Тогда система (3.30) принимает вид:
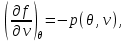
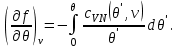 (3.31)
(3.31)Решение системы (3.31) позволяет найти удельную свободную энергию в виде
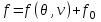 (3.32)
(3.32)Начало
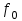 отсчета удельной свободной энергии также может быть найдено из условий при
отсчета удельной свободной энергии также может быть найдено из условий при 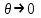 :
: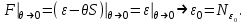
Тогда (3.32) принимает вид:
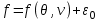 , (3.33а)
, (3.33а)а выражение всей свободной энергии системы с точностью до аддитивной постоянной принимает вид:
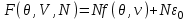 (3.34)
(3.34)Тогда реакция системы на включение внешнего поля задается дополнительным уравнением состояния, которое в зависимости от набора переменных состояния имеет вид:
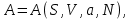 или
или 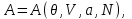
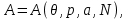
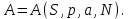 (3.35)
(3.35)Тогда изменение соответствующего термодинамического потенциала, связанное с включением нуля от нуля до
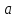 , определяется из выражений :
, определяется из выражений :
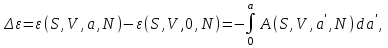
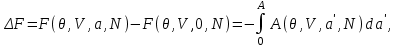 (3.36)
(3.36)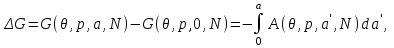
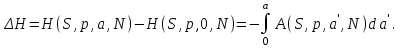
Таким образом, задание термодинамического потенциала в макроскопической теории возможно только на основе использования заданных уравнений термодинамического состояния, которые в свою очередь, сами получаются на основе задания термодинамических потенциалов. Разорвать этот “замкнутый круг” можно только на основе микроскопической теории, в которой состояние системы задается на основе функций распределения с учетом статистических особенностей.
3.
Обобщим полученные результаты на случай многокомпонентных систем. Это обобщение осуществляется путем замены параметра
 множеством
множеством 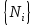 . Рассмотрим сказанное на конкретных примерах.
. Рассмотрим сказанное на конкретных примерах.Положим, что термодинамическое состояние системы задано параметрами
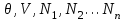 , т.е. мы рассматриваем систему в термостате, состоящую из нескольких компонентов, число частиц в которых равно
, т.е. мы рассматриваем систему в термостате, состоящую из нескольких компонентов, число частиц в которых равно 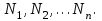 Свободная энергия, являющаяся в этом описании термодинамическим потенциалом, имеет вид:
Свободная энергия, являющаяся в этом описании термодинамическим потенциалом, имеет вид: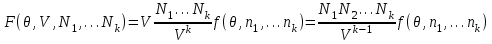 (3.37)
(3.37)В качестве аддитивного параметра в (3.37) введены не число частиц, а объем системы V. Тогда через
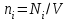 обозначена плотность системы. Функция
обозначена плотность системы. Функция 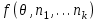 является неаддитивной функцией неаддитивных аргументов. Это достаточно удобно, поскольку при разбиении системы на части функция
является неаддитивной функцией неаддитивных аргументов. Это достаточно удобно, поскольку при разбиении системы на части функция 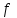 не изменится для каждой части.
не изменится для каждой части.Тогда для параметров термодинамической системы можно записать:
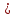
Учитывая, что
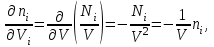 имеем
имеем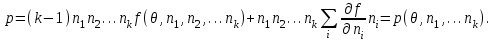 (3.38)
(3.38)Для химического потенциала отдельного компонента запишем:
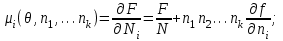 (3.39)
(3.39)Существуют и другие способы учета аддитивных свойств свободной энергии. Введем относительные плотности чисел частиц каждой из компонент:
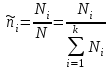 , (3.40)
, (3.40)не зависящие от объема системы V. Здесь
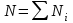 - общее число частиц в системе. Тогда
- общее число частиц в системе. Тогда 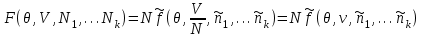 (3.41)
(3.41)Выражение химического потенциала в этом случае принимает более сложный вид:
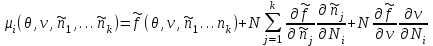
Вычислим производные
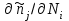 и
и 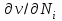 и подставим их в последнее выражение:
и подставим их в последнее выражение:
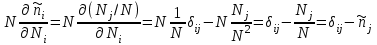
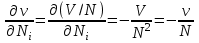
Тогда
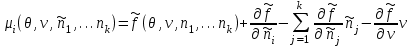 (3.42)
(3.42)Выражение для давления, напротив упростится:
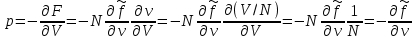 (3.43)
(3.43)Аналогичные соотношения могут быть получены и для потенциала Гиббса. Так, если в качестве аддитивного параметра задан объем, то с учетом (3.37) и (3.38) запишем:
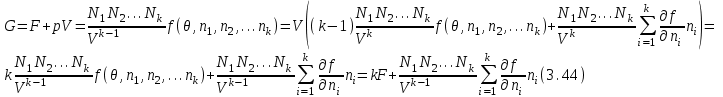 это же выражение может быть получено из (3.юю), которое в случае многих частиц принимает вид:
это же выражение может быть получено из (3.юю), которое в случае многих частиц принимает вид: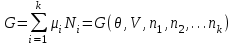 (3.45)
(3.45)Подставляя в (3.45) выражение(3.39), находим:
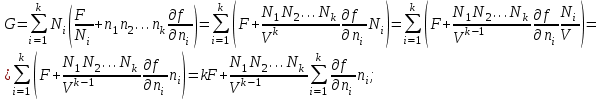
что полностью совпадает с (3.44).
Для того, чтобы перейти к традиционной записи потенциала Гиббса (через переменные состояния (
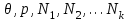 )) необходимо разрешить уравнение (3.38):
)) необходимо разрешить уравнение (3.38):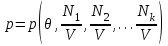
Относительно объема V и подставить результат в (3.44) или (3.45):
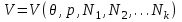
Если в качестве аддитивного параметра задано полное число частиц в системе N, то потенциал Гиббса с учетом (3.42) принимает следующий вид:

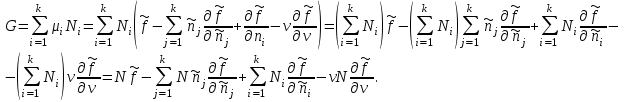
Зная вид удельных величин:

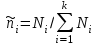 ,получим:
,получим: