ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
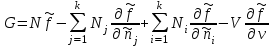.В последнем выражении суммирование по jзаменим на суммирование по i. Тогда второе и третье слагаемые в сумме дают нуль. Тогда для потенциала Гиббса окончательно получим:
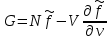. (3.46)Это же соотношение может быть получено и другим способом (из (3.41) и (3.43)):
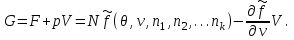
Далее рассмотрим многокомпонентную систему “под поршнем”, состояние которой описывается параметрами (
). Роль термодинамического потенциала в этом случае играет потенциал Гиббса:
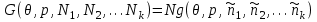(3.47)Тогда для химического потенциала каждой из компонент получим:
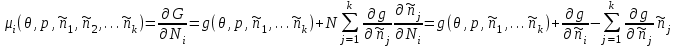(3.48)При выводе (3.48) выполнены преобразования, аналогичные использованным при выводе (3.42), с помощью воображаемых стенок. Параметры состояния системы образуют набор (
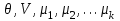).Роль термодинамического потенциала играет потенциал
, который принимает вид: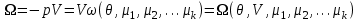
(3.49)Как видно из (3.49), единственным аддитивным параметром в данном случае является объем системы V.
Определим некоторые термодинамические параметры такой системы. Число частиц в данном случае определяется из соотношения:
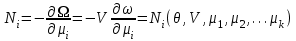(3.50)Для свободной энергии F и потенциала Гиббса G можно записать:
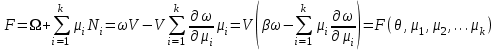(3.51)
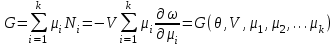(3.52)Таким образом, соотношения для термодинамических потенциалов и параметров в случае многокомпонентных систем видоизменяются только за счет необходимости учета числа частиц (или химических потенциалов) каждой компоненты. При этом сама идея метода термодинамических потенциалов и расчетов, проводимых на его основе, остается неизменной.
4.
В качестве примера использования метода термодинамических потенциалов рассмотрим задачу химического равновесия. Найдем условия химического равновесия в смеси трех веществ, вступающих реакцию. Дополнительно предположим, что исходные продукты реакции является разреженными газами(это позволяет не учитывать межмолекулярные взаимодобывания), а в системе поддерживаются постоянные температура и давление
, 
(такой процесс наиболее просто реализовать практически, поэтому условие постоянства давления и температуры создаются в промышленных установках для химической реакции ).Условие равновесия термодинамической системы в зависимости от способа ее описания определяются максимальной энтропией системы или минимальной энергией системы (подробнее см. Базаров Термодинамика). Тогда можно получить следующие условия равновесия системы:
-
Состояние равновесия адиабатически изолированной термодинамической системы, заданной параметрами (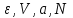
), характеризуется максимумом энтропии:
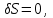
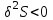(3.53а)Второе выражение в (3.53а) характеризует устойчивость равновесного состояния.
-
Состояние равновесия изохорно-изотермической системы, заданное параметрами (
), характеризуется минимумом свободной энергии. Условие равновесия в этом случае принимает вид:
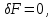
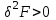(3.53б)-
Равновесие изобарно-изотермической системы, задаваемой параметрами (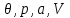
), характеризуется условиями:
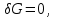
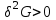(3.53в)-
Для системы в термостате с переменным числом частиц, определенной параметрами (
), условия равновесия характеризуется минимумами потенциала :
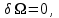
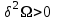(3.53г)Перейдем к использованию химического равновесия в нашем случае.
В общем случае уравнение химической реакции записывается в виде:
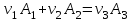(3.54)Здесь
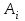- символы химических веществ, 
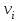- так называемые, стехиометрические числа. Так, для реакции
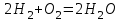
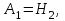
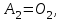
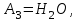
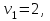
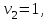
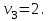
Поскольку в качестве параметров системы выбраны давление и температура, которые положены постоянными. Удобно в качестве состояния термодинамического потенциала рассмотреть потенциал Гиббса G. Тогда условие равновесия системы будет заключаться в требовании постоянства потенциала G:
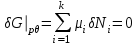(3.55)Поскольку мы рассматриваем трехкомпонентную систему, положим
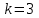. Кроме того, учитывая (3.54), можно записать уравнение баланса для числа частиц (
): 
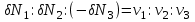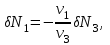
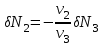(3.56)Вводя химические потенциалы для каждой из компонент:
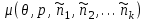и учитывая сделанные допущения, находим:
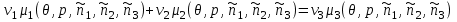(3.57)Уравнение (3.57) было впервые получено Гиббсом в 1876г. и является искомым уравнением химического равновесия. Легко заметить, сравнивая (3.57) и (3.54), что уравнение химического равновесия получается из уравнения химической реакции путем простой замены символов реагирующих веществ на их химические потенциалы. Этот прием может быть использован и при записи уравнения химического равновесия для произвольной реакции.
В общем случае решение уравнения (3.57) даже для трех компонент является достаточно загруженным . Это связанно, во-первых, с тем, что даже для однокомпонентной системы получить явные выражения для химического потенциала весьма затруднительно. Во-вторых, относительные концентраци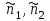и
и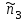 
не являются малыми величинами. То есть невозможно выполнить по ним разложение в ряд. Это еще сильнее усложняет задачу решения уравнения химического равновесия.Физически отмеченные трудности объясняются необходимостью учета перестройки электронных оболочек атомов, вступающих в реакцию. Это приводит к определенным сложностям микроскопического описания , что сказывается и при макроскопическом подходе.
Поскольку мы условились ограничится исследованием разреженности газа, то можно воспользоваться моделью идеального газа. Будем считать, что все реагирующие компоненты являются идеальными газами, заполняющими общий объем и создающие давление p. В этом случае любым взаимодействием (кроме химических реакций) между компонентами смеси газов можно пренебречь. Это позволяет допустить, что химический потенциал i-го компонента зависит только от параметров этого же компонента.
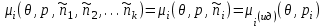(3.58)Здесь
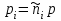- парциальное давление i-го компонента, причем: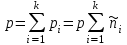
С учетом (3.58) условие равновесия трехкомпонентной системы (3.57) примет вид:
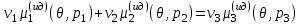(3.59)Для дальнейшего анализа воспользуемся уравнением состояния идеального газа, которое запишем в виде:
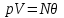(3.60)Здесь через
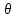, как и ранее, обозначается термодинамическая температура 
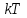. Тогда известная из школы запись 
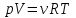принимает вид: 
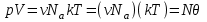, что и записано в (3.60).Тогда для каждого компонента смеси получим:
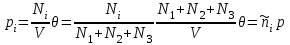(3.61)Определим вид выражения химического потенциала идеального газа. Как следует из (2.22), химический потенциал имеет вид:
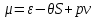(3.62)Учитывая уравнение (3.60), которое можно записать в виде
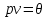, задача определения химического потенциала сводится к определению удельной энтропии и удельной внутренней энергии.
Система уравнений для удельной энтропии следует из термодинамических тождеств (3.8) и выражения теплоемкости (3.12):
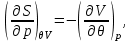
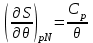
Учитывая уравнение состояния (3.60) и переходя к удельным характеристикам, имеем:
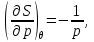
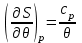(3.63)Решение (3.63) имеет вид:
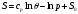
Система уравнений для удельной внутренней энергии идеального газа следует из (2.23):
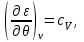
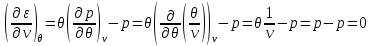
Решение этой системы запишется в виде:
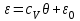
Подставляя (3.64) - (3.65) в (3.66) и учитывая уравнение состояния идеального газа, получаем:
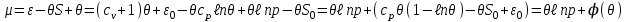(3.66)Для смеси идеальных газов выражение (3.66) принимает вид:
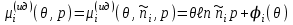
Подставляя (3.67) в (3.59), получаем:
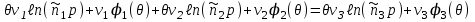
Выполняя преобразования, запишем:
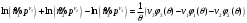
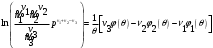
Выполняя потенцирование в последнем выражении, имеем:
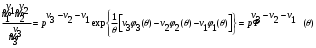(3.68)Соотношение (3.68) получило название закона действующих масс. Величина
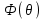является функцией только температуры и получила название компоненты химической реакции.Таким образом химическое равновесие и направление химической реакции определяется величиной давления и температуры.