Файл: Цель работы Изучить способы аппроксимации функции плотности вероятности по данным наблюдений. Задачи.docx

Аппроксимация плотности вероятности

Цель работы

Изучить способы аппроксимации функции плотности вероятности по данным наблюдений.

Задачи

1. Сгенерировать выборку случайных чисел.

2. Сформировать локальные оценки логарифма плотности вероятности по полученной выборке значений случайной величины.

3. По новой выборке локальных оценок логарифма плотности выполнить аппроксимацию функции плотности;



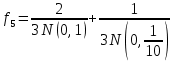
Исходные параметры для функции аппроксимации заданы в таблице 1.

n	A	a	lampda	g
200	[0.66; 0.33]	[0; 0]	[1; 0.1]	'N'

Ход работы

М-файл для работы представлен на рис. 2.

n = 200 A = [0.66 0.33]; a = [0 0]; lambda = [1 0.1]; g = 'N'; Approxpdf(n, A, a, lambda, g)

Рис. 2. М-файл для работы

Используя функцию Approxpdf(n,A,a,lampda,g), были получены локальные оценки логарифма плотности (см. рис. 3).



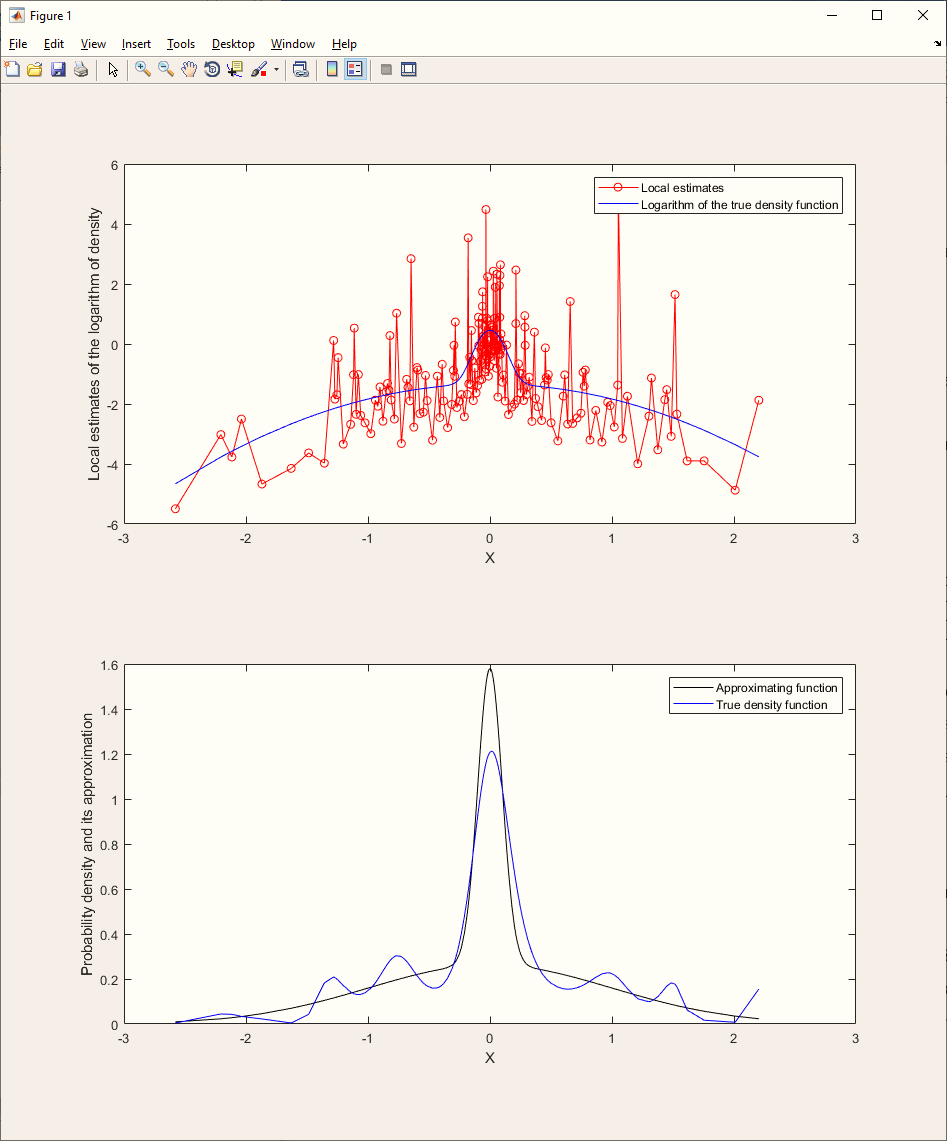
Рис. 3. Формирование локальных оценок логарифма плотности

На рис. 4 показаны результаты аппроксимации по полученным локальным оценкам.



Рис. 4. Результаты аппроксимации

Вывод

В процессе выполнения данной работы были изучены различные методы приближения функции плотности вероятности на основе имеющихся наблюдений. Для этого была создана выборка случайных чисел, на основе которой были получены локальные оценки логарифма плотности вероятности. Затем была создана новая выборка на основе этих оценок, и с ее помощью была выполнена аппроксимация функции плотности, указанной в задании.

---

function Approxpdf(n,A,a,lampda,g) X=GenRandom(n,A,a,lampda,'N'); [xv,fv,fz,m]=approx(X,1);

F=Truepdf(xv,A,a,lampda,'N');

subplot(211); plot(xv,log(fv),'ro-',xv,log(F),'b'); xlabel('X'); ylabel('log f'); legend('LF','LF*');

% n	объем-выборка
% R	Равномерное	N	Нормальное
% L	Логистическое	E	Экспоненциальное
% G	Гамма (хи-квадрат)

subplot(212); plot(xv,F,'k',xv,fz,'b-'); xlabel('X'); ylabel('f'); legend('F','F*'); function X=GenRandom(n,A,a,lampda,g)


% где A=[A1 A2 ...Am]

% a=[a1 a2...am] lampda=[lampda1 lampda2 ...lampdam]

% если f = 0.5N(5,1)+0.5N(11,2)

% A=[0.5 0.5] a=[5 11] lampda=[1 2] X=[];

for i=1:length(A) ni=n*A(i); switch g

case 'R'

Xi=a(i)+ lampda(i)*rand(ni,1); case 'N';

Xi=a(i)+ lampda(i)*(sqrt(-2*log(rand(ni,1)))).*sin(2*pi*rand(ni,1)); case 'E'

Xi=a(i)- lampda(i) *log(rand(ni,1)); case 'L'

Xi=a(i)+lampda(i)*log((1-rand(ni,1))./rand(ni,1)); case 'G'

ng=input(['n',num2str(i),'\n']); for j=1:ni

Xi(j)=a(i)+ lampda(i)*sum((randn(ng,1)).^2)/2; end

end

if size(Xi,2)>size(Xi,1) Xi=Xi';

end X=[X;Xi];

end

X=sort(X);
function F=Truepdf(X,A,a,lampda,g) F=0;

for i=1:length(A) switch g

case 'N';

F=F+A(i)*exp(-0.5*((X-a(i))/lampda(i)).^2)/(sqrt(2*pi)*lampda(i)); case 'E'

F=F+A(i)*exp(-(X-a(i))/lampda(i))/lampda(i); case 'L'

z=(X-a(i))/lampda(i); F=F+A(i)*1/lampda(i)*exp(-z)./(1+exp(-z)).^2;

case 'G'

n=input(['n',num2str(i),'\n']);

F=F+A(i)*(X-a(i)).^(n/2-1)/(lampda(i)^(n/2)*gamma(n/2)).*exp(-(X-a(i))/lampda(i)); end

end
function [xv,fv,fz,m]=approx(x,criteria)

% Дубов И.Р. Аппроксимация вероятностных законов в системах мониторинга:

% Владимир, 2001. –137с.

% criteria=0 или 1

x=sort(x); % упорядоченная выборка

n=length(x); for i=1:(n-1)

xv(i)=(x(i)+x(i+1))/2; end

xv=xv'; k=1:n;

d=sum(k.^-2); % Дисперсия ошибок

M=-1*sum(k.^-1); % пси-функция Эйлера (дигамма – функция) nr=n-1;

for i=1:nr fv(i)=exp(M)/(x(i+1)-x(i));

end

---

fv=fv'

lfv=log(fv); % lfv локальные оценок логарифма плотности вероятности

% Аппроксимация логарифма плотности

if criteria==0 [m,fest,lfz,a]=Malloca(xv,lfv,d);

else

for i=1:n-1 [yest,fest]=fit(xv,lfv,'x',i-1,1);

f(i)=abs(mean((lfv-yest).^2)-d);

j=i+1; [yest,fest]=fit(xv,lfv,'x',j-1,1);

c=abs(mean((lfv-yest).^2)-d); if c>f(i)

break; end

end m=i-1;

[lfz,fest]=fit(xv,lfv,'x',m,1); end

fz=exp(lfz);
function [yest,fest,a]=fit(x,y,f,m,s)

% y=X1(x)+X2(x)+X3(x) … +Xm(x)+error of std s

% where Xj(x) bases function

% A=[X1(x) X2(x) X3(x) … Xm(x)]

% % size of A is N*M

% for example if y(x)=a_0+a_1*x+a_2*x^2 … a_m*x^m

% A=[1 X X^2 … X^m]

% a=[a_0 a_1 … a_m]

% where X=[x_1 x_2 … x_n]'
if size(x,2)>size(x,1) x=x';

end

if size(y,2)>size(y,1) y=y';

end

if size(s,2)>size(s,1) s=s';

end n=length(x); s=s.*ones(n,1); si=1./s;

sg=sqrt(1/mean(si.^2)); sb=si*sg; Af=zeros(n,m+1);

for i=0:m Af(:,i+1)=(((eval(f)).^i));

end sa=sb(:,ones(1,m+1)); A=Af.*sa; alpha=A'*A;

b=y.*sb; Beta=A'*b; a=inv(alpha)*Beta; yest=Af*a;

fest=[num2str(a(1))]; for i=2:length(a)

fest=[fest,'+',num2str(a(i)),'*',f,'.^',num2str(i-1)]; end

%fest=['y=',fest]; temp=fest; n=length(temp)-1; j=1;

i=1;

while (j
if (temp(j)=='+')&(temp(j+1)=='-') fest(i)=[];

i=i-1; end i=i+1; j=j+1;

end
function [degree,fest,LF,a]=Malloca(xf,lfv,sd2)

%==================================================

% malloca criteria

% c=abs(mean((lfv-yest).^2)-d*(1-2*(j-1)/n))

%==================================================

n=length(xf); sd=sd2.^0.5; for i=2:n

[yest,fest]=fit(xf,lfv,'x',i-1,sd); f(i)=sum(((yest-lfv).^2)./sd2)-(n-2*(i-1)); j=i+1;

[yest,fest,a]=fit(xf,lfv,'x',j-1,sd);

c=sum(((yest-lfv).^2)./sd2)-(n-2*(j-1)); if c>f(i)

break; end

end degree=i-1;

[yest,fest,a]=fit(xf,lfv,'x',degree,sd); LF=yest;

---