Файл: Занятие 5 Цель работы Ознакомление с теоремой В. А. Котельникова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 34
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЭС Тема 17 Практическое занятие 5
Цель работы: Ознакомление с теоремой В.А. Котельникова
Влади́мир Алекса́ндрович Коте́льников — советский и российский учёный в области радиофизики, радиотехники, электроники, информатики, радиоастрономии и криптографии.
Владимир Александрович Котельников - действительный член АН, вице-президент АН СССР, дважды Герой Социалистического труда, лауреат Государственной и Ленинской премий, профессор родился в Казани в семье профессора Казанского университета в 1908 году.
После окончания школы он поступил в Московский энергетический институт, который закончил в 1931 году, получил специальность инженера-электрика и начал работать инженером в институте связи Красной Армии, затем перешел в Центральный научно-исследовательский институт наркомата связи и одновременно стал работать в МЭИ. На начальном пути своей научной деятельности он занимался проблемами увеличения эффективности систем связи.
В 1933 году он уже публикует свою крупную научную работу «О пропускной способности эфира и проволоки в электросвязи», в которой впервые сформулирована теорема (известная в радиотехнике как теорема Котельникова) о точном представлении функции с ограниченным спектром совокупностью ее отсчетов, произведенных в отдельно взятых точках. Она широко применяется в радиофизике, оптике, в теории цифровой обработки сигналов.
Для деятельности В.А. Котельникова характерна тесная связь теории с практикой. Под его руководством в довоенные годы была создана аппаратура однополосной радиосвязи на линии Москва-Хабаровск. В годы Великой Отечественной войны в руководимом им коллективе были разработаны новые системы связи. За эти разработки В.А. Котельников в 1943 г. и 1946 г. был дважды удостоен Государственной премии СССР. Позднее с его участием были созданы первые образцы аппаратуры управления и контроля состояния космических аппаратов.
Широкую известность, как у нас, так и за рубежом принесла Котельникову В.А. фундаментальная работа «Теория потенциальной помехоустойчивости», опубликованная в 1947 году, где установлены предельные возможности радиоприема при наличии шумов.
В 1953 году В.А. Котельников избирается действительным членом АН СССР
, а с 1954 по 1988 годы возглавляет Институт радиотехники и электроники АН СССР, где его идеи в области приема сигналов послужили основой для создания нового научного направления – планетной радиолокации. Стимулом к развитию этого направления явилась необходимость уточнения размеров Солнечной системы для осуществления полетов космических кораблей к планетам. Радиолокация планет Венеры, Марса, Меркурия в1961-1964 годах позволила получить основополагающие данные о физическом состоянии этих планет – период и направление вращения Венеры, коэффициенты отражения поверхности планет. За эти работы В.А. Котельников и его сотрудники были удостоены Ленинской премии.
После ряда фундаментальных исследований в 1984 –1992 годах, впервые в мире осуществлено картографирование северной части планеты Венера с помощью АМС «Венера 15» и «Венера 16». Работа проводилась многими коллективами страны, в том числе ИРЭ АН СССР и ОКБ МЭИ, который был создан Котельниковым В.А. и до перехода на работу в Институт радиотехники и электроники АН СССР, он возглавлял это КБ.
Академик В.А. Котельников – основатель теории потенциальной помехоустойчивости. Всемирную известность и широкое использование получила теорема отсчетов (теорема Котельникова). Разработал основы и создал аппаратуру телеметрии для самолетов и ракет, а также радиолокации планет Солнечной системы. Сыграл большую роль в развитии отечественной науки как директор Института радиоэлектроники РАН и вице-президент РАН, основатель ОКБ МЭИ.
Теорема Котельникова гласит о том, что непрерывный сигнал с ограниченным спектром можно точно восстановить по его дискретным отсчётам, если они были взяты с частотой дискретизации, превышающего максимальную частоту сигнала минимум в два раза.
Теорема Котельникова
Возможность передачи непрерывного сигнала его дискретными отсчетами была обоснована В. А. Котельниковым в 1933 г. В соответствии с его теоремой любой непрерывный сигнал, ограниченный по спектру верхней частотой Fв, полностью определяется последовательностью своих дискретных отсчетов, взятых через промежуток времени Тд≤1/2Fв.
Таким образом, если требуется передать непрерывный сигнал U(t) с ограниченным спектром, то не обязательно передавать весь сигнал, а
достаточно передать лишь его мгновенные значения, отсчитанные через интервалы времени Тд . В соответствии с этим частота следования дискретных отсчетов сигнала, т. е. частота дискретизации 2Fв≤ Fд.
Для восстановления непрерывного сигнала из последовательности его дискретных отсчетов в пункте приема используется фильтр нижних частот (ФНЧ) с частотой среза, равной Fв.
Как известно, отклик идеального ФНЧ с граничной частотой среза Fв на очень короткий прямоугольный импульс, поданный на его вход, имеет вид, изображенный на рисунке 1 .
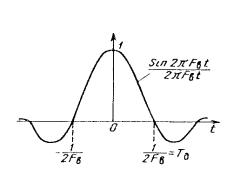
Рисунок 1 . Отклик ФНЧ на короткий прямоугольный импульс.
Если на вход такого фильтра поступает последовательность коротких импульсов, соответствующих дискретным отсчетам непрерывного сигнала (рисунок 2), то на выходе фильтра в результате суммирования отдельных откликов переданный непрерывный сигнал вновь восстанавливается.
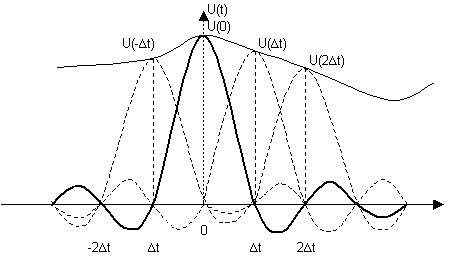
Рисунок 2. Формирование непрерывного сигнала фильтром нижних частот.
Выбор частоты дискретизации
На основании теоремы Котельникова Fд >=2Fв. Если выбрать Fд = 2Fв, то, как видно из рисунка 3, нижняя боковая частота, определяемая из условия:
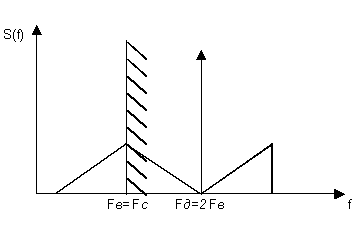
Рисунок 3. Выбор частоты дискретизации.
Fд –Fв=2Fв-Fв=Fв совпадает с верхней частотой спектра модулирующего сигнала и для восстановления непрерывного сигнала из последовательности его дискретных отсчетов необходимо использовать идеальный ФНЧ с частотой среза Fc=Fв. В реальных системах частоту дискретизации выбирают из условия Fд>2Fв. Обычно Fд=(2,3...2,4)Fв. Так, при дискретизации телефонных сигналов с диапазоном частот 0,3...3,4 кГц частота дискретизации равна 8 кГц (рисунок 4).
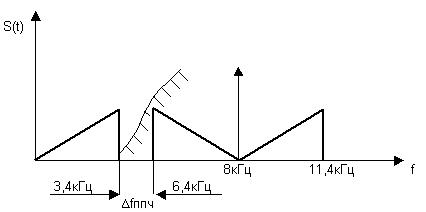
Рисунок 4. Выбор частоты дискретизации.
В данном случае упрощаются требования к параметрам ФНЧ, так как при этом образуется достаточно широкая (1,2 кГц) переходная полоса частот Δfппч для расфильтровки, которая позволяет использовать простые ФНЧ на приеме для восстановления непрерывного сигнала из последовательности его дискретных отсчетов.
Квантование по уровню
На рисунке 1.5 показаны отсчеты (дискреты) сигнала и их квантованные значения. В результате квантования передаются не истинные, а только разрешенные значения уровней.
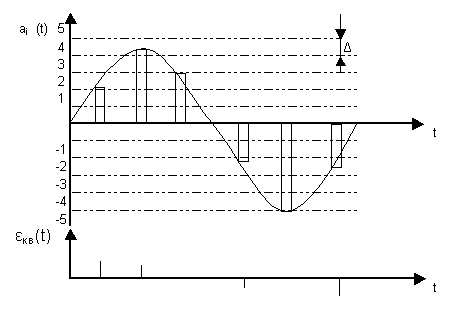
Рисунок 5. Квантования сигнала.
На рисунке 5: Δ - шаг квантования; E кв(t) - ошибка квантования.
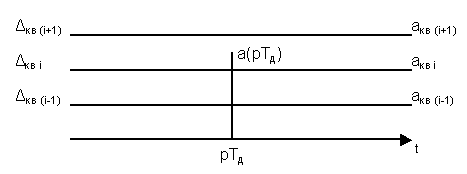
Рисунок 6. Квантование.
Вместо a(pТд) передается aкв (i+1) или aкв i значения. Возникает ошибка квантования ?кв:
E кв i (pТд)= a(pТд) - aкв i (рисунок 1.12)
Квантование бывает:
-
равномерное (Δ i = Δ i-1 = Δ i-2 =? );
-
неравномерное.
В первом случае возможны два типа амплитудных характеристик (АХ) квантующих устройств. Они приведены на рисунке 7.
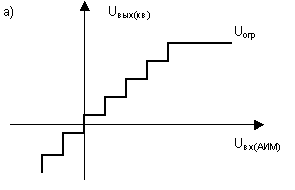
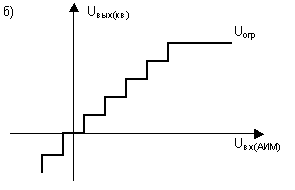
Рисунок 7. АХ квантующих устройств.
При АХ, изображенной на рисунке 7.а, возникают шумы в режиме молчания
, а при АХ, изображенной на рисунке 7.б, не воспроизводятся малые сигналы 
.Расчет мощности шумов квантования.
Ошибку квантования Eкв(t) можно рассматривать как некоторую помеху – шум квантования. Влияние его на качество связи можно оценить отношением:
где Rкв – коэффициент шума квантования;
Рср.с – средняя мощность сигнала;
Ркв – мощность шума квантования.
Eкв(t) – последовательность прямоугольных импульсов с частотой Fд и случайной высотой. Полагаем, что t<<Тд.
Eкв(t) – случайная величина с плотностью вероятности Wкв(х).
Заметим, что при неравномерном квантовании Ркв можно уменьшить, если для больших рi выбирать меньшие Δi, то есть для тех шагов квантования, где вероятность появления сигнала больше, выбирать меньший шаг квантования. Таким образом, при равномерном квантовании Ркв зависит только от Δ. Поэтому Rкв зависит только от мощности отсчета сигнала. Для того, чтобы не возникали шумы ограничения Uогр=Umax, где Umax - пиковые значения сигнала.
Определение числа уровней квантования.
Энергетический спектр шумов квантования, то есть последовательности импульсов случайной амплитуды, но детерминированной частоты Fд и длительности tи, примерно равномерен в очень широкой полосе частот, если t<<Тд, то мощность этих шумов пропорциональна полосе частот Δf, в которой она определяется.
На приеме исходный сигнал выделяется ФНЧ с граничной частотой Fв, который уменьшает мощность шума квантования Ркв в раз
, то есть:
Для речевых сигналов
дБ. Однако, учитывая разную длину абонентских линий,
определяется как разность уровней мощности пиковых значений мощности на входе канала и средней мощности наиболее удаленного абонента. Тогда 
дБ.Исходя из нормирования помех, можно определить необходимое число уровней квантования:
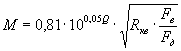
Защищенность от шумов квантования не должна быть меньше 25 дБ. Тогда . Подставив в формулу [1-14] Fд=8 кГц, Fв =3,4 кГц,
дБ, получим 
, что существенно усложняет возможности передачи ИКМ-сигнала.При неравномерном квантовании шаг квантования изменяется по определенному закону. Если уменьшать шаг квантования для более вероятных значений сигнала, то мощность шума квантования уменьшается. Однако, при этом вид АХ квантующего устройства зависит от закона распределения квантуемого сигнала. Поэтому обычно неравномерное квантование обеспечивает примерное постоянство Rкв для различных значений квантованных отсчетов сигнала.