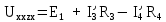Файл: Контрольная работа по дисциплине тоэ вариант 39 студент группы эпзу101 Кувшинов Д. В. Проверил преподаватель.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 100

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской ФедерацииИркутский Государственный Технический УниверситетКафедра общеобразовательных дисциплин Контрольная работапо дисциплине ТОЭВариант №39Выполнил: студент группы ЭПзу-10-1Кувшинов Д. В.Проверил: преподаватель Васильева Ф. А.Иркутск 2012Вариант 13.Задание 1. Линейные электрические цепи постоянного тока.Для электрической схемы, изображенной на рис. 12 выполнить следующее:

  1. Упростить схему, заменив последовательно и параллельно соединенные резисторы четвёртой и шестой ветвей эквивалентными.

  2. Заменить источники тока эквивалентными источниками ЭДС.

  3. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

  4. Определить токи во всех ветвях схемы методом контурных токов.

  5. Определить токи во всех ветвях схемы методом узловых потенциалов.

  6. Результаты расчета токов, выполненного двумя методами, свести в таблицу и сравнить их между собой.

  7. Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

  8. Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора.

  9. Рассчитать потенциалы точек любого замкнутого контура, включающего в себя обе ЭДС и построить потенциальную диаграмму для любого замкнутого контура.

Дано:

R1 = 22,5 Ом

R2 = 18 Ом

R3 = 15 Ом

R`4 = 135 Ом

R``4 = 15 Ом

R5 = 12 Ом

R`6 = 5,5 Ом

R``6 = 5 Ом

E1 = 24 В

E2 = 30 В

J1 = 0,2A

J2 = 0A
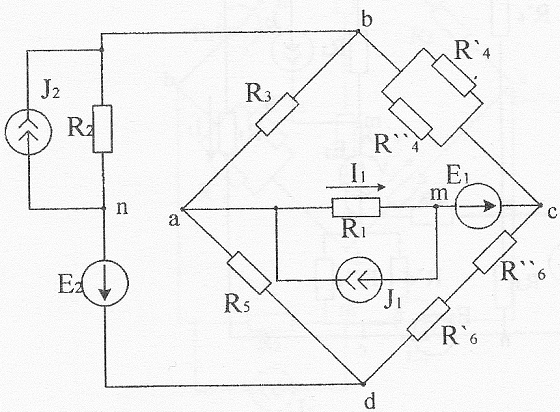
Рисунок 12 – Схема цепи

  1. Упростим схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет будем вести для упрошенной схемы, а такжеисточники тока эквивалентными источниками ЭДС.
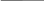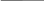
ЗдесьE`1 = J1 ×R1 = 0,2 ×22,5 = 4,5 BИсточник тока можно исключить из схемы т.к. R6 = R’6 + R’’6 = 5,5 + 5 = 10,5 OмR’4R’’4 R4 = = 13,5 Ом 4R’4+ R’’4В этой схеме:Узлов У = 4Ветвей В = 6Контуров К = 3

  1. Составим на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.
Выберем направление токов в ветвях схемы произвольно.Количество уравнений необходимых по законам Кирхгофапо первому закону n1 = У – 1 = 4 – 1 = 3;по второму закону n2 = K = 3;общее количество n = n1 + n2 = 3 + 3 = 6.По первому закону Кирхгофадля узла “a”: I5 – I1 – I3 = 0дляузла“b”: I3+ I4 – I2 = 0дляузла“c”: I1 – I4 – I6 = 0По второму закону Кирхгофадля контура I: I1× R1 + I4× R4 – I3× R3 = E1 – E`1для контура II: -I1× R1 – I5× R5 – I6
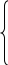
× R6 = E`1 – E1для контура III: I2× R2 + I5× R5 + I3× R3 = E2Запишем систему уравнений поставив числовые значенияI5 – I1 – I3 = 0I3 + I4 – I2 = 0I1 – I4 – I6 = 022,5 × I1 + 13,5× I4 –15×I3 = 24 – 4,5 = 19,5-22,5× I1-12× I5 -10,5× I6 = 4,5-24=-19,518× I2+12×I5+ 15× I3 = 30

  1. Решим систему уравнений составленную на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы с помощью MathCad методом итераций.

  1. Определить токи во всех ветвях схемы методом контурных токов.
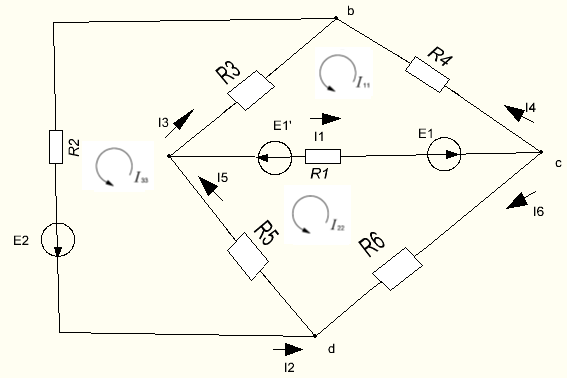
При расчете цепей методом контурных токов принимаем, что в каждом независимом контуре течет свой контурный ток.Число уравнений, которые необходимо составить для расчёта токов в ветвях схемы, всегда равно числу независимых контуров. В данной схеме три независимых контура, поэтому имеем следующую систему:I11×(R1+ R3 + R4) – I33× R3 – I22× R1 = E1 – E`1I22×(R1 + R5 + R6) – I11× R1 – I33× R5 = E`1 – E1I33×(R2+ R3 + R5) – I22× R5 – I11× R3 = E2Подставим числовые значения:
51×I11 – 22,5×I22 – 15×I33= 19,5-22,5×I11+45×I22– 12×I33 = -19,5-15×I11– 12×I22+45×I33= 30Решим систему уравнений с помощью MathCad методом итераций:





Найдем токи цепи:

I1=I11-I22=0,761-0,207=0,554 А;

I2=I22=0,975 А;

I3=I33-I11=0,975-0,761=0,214 А;

I4= I11=0,761 А;

I5= I33-I11=0,975-0,207=0,768 А;

I6= -I22= -0,207 А.

Отрицательное значение тока означает, что действительное значение тока не совпадает с первоначально выбранным.


  1. Результаты расчета токов, выполненного двумя методами, сведем в таблицу и сравним их между собой.

Номер тока по схеме
Значение, полученное по законам Кирхгофа, А
Значение, полученное методом контурных токов, А
Разница

1
0,554
0,554
0

2
0,975
0,975
0

3
0,215
0,214
0,001

4
0,761
0,761
0

5
0,768
0,768
0

6
-0,207
-0,207
0

  1. Составим баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).
Суммарная мощность источников:∑Pист.=E1×I1 – E`1×I1 +E2×I2=24×0,554 – 4,5×2,493+30×0,975=40,053ВтСуммарная мощность потребителей:∑Pпотр=R1×I1
2+R2×I22+R3×I32+R4×I42+R5×I52+R6×I62==22,5×0,5542+18×0,9752+15×0,2152+13,5×0,7612+12×0,7682+10,5×(-0,207)2= 40,056171Вт

  1. Определим ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора.
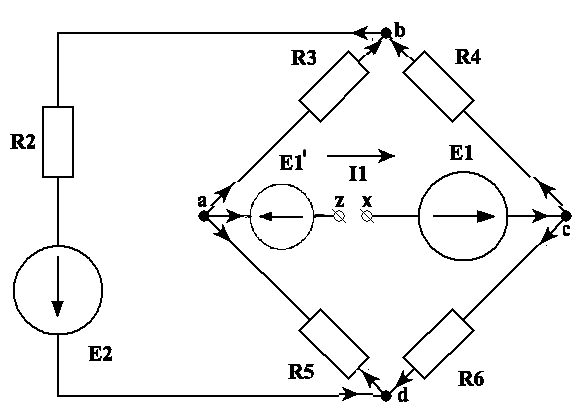
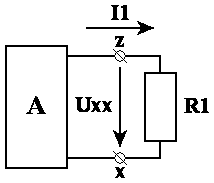
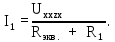
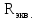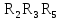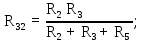
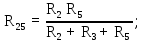
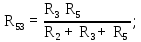
Выделим из схемы ветвь, в которой необходимо определить ток:Оставшуюся часть схемы представим в виде активного двухполюсника к зажимам z, x которого присоединена выделенная ветвь:Согласно теореме об эквивалентном генераторе, по закону Ома, составим уравнение:Н айдем активного двухполюсника, для этого преобразуем треугольник в эквивалентную звезду: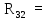6 Ом;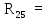4,8 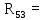Ом;4 Ом;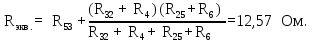Найдем 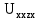активного двухполюсника методом узловых потенциалов: 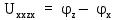; 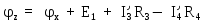+E’1

Смотрите также файлы