НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ПРОЧНОСТИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ

УТВЕРЖДАЮ

Преподаватель

________________ 2020 г.

З А Д А Н И Е №1

«Расчет статически определимого ступенчатого стержня»

Шифр зачетной книжки:


РАЗРАБОТАЛ:

Студент:

Группа:

Факультет:

Новосибирск

2020
Задача 1. Расчет статически определимого ступенчатого стержня

Ступенчатый стержень изготовлен из серого чугуна марки СЧ24 с пределами прочности при растяжении 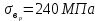и сжатии 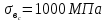, модулем упругости 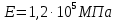(рис. 1).

Исходные данные к задаче

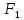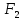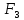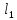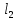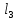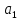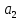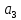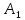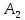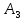кН			м						см2				-
40	-70	30	0,2	0,6	0,9	0,1	0,4	0,9		3	2	1		3,7

---

Требуется:

1) построить эпюры нормальных (продольных) сил, нормальных напряжений и перемещений поперечных сечений;

2) определить перемещение свободного торца стержня, используя принцип независимости действия сил;

3) проверить прочность стержня.



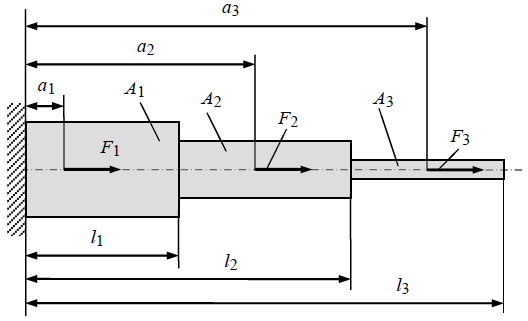
Рис. 1. Расчетная схема к задаче 1


Решение

Расчетная схема. Расчетная схема стержня согласно исходным данным к задаче изображена на рис. 2. Начало системы координат xy поместим в точке B (заделка). Ось х направим вдоль стержня (горизонтально), ось y – перпендикулярно оси х (вертикально).

Определение реакции опоры. Предполагаем, что реакция опоры (заделки) R_Bнаправлена в положительном направлении оси х (рис. 2). Для нахождения реакции составляем уравнение равновесия:





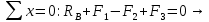
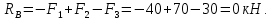
Эпюра нормальных сил. Разобьем стержень на отдельные (силовые) участки, начиная от свободного торца. Границами участков при построении эпюры нормальных сил являются сечения, в которых приложены внешние сосредоточенные силы, а также торцы стержня (сечения B и M). Таким образом, заданный стержень имеет три участка – MK, KC, CB (рис. 2). При применении метода сечений принципиально безразлично, равновесие какой из отсеченных частей (левой или правой) стержня рассматривать. В данном случае, применяя метод сечений, будем оставлять правую и отбрасывать левую отсеченную часть стержня. При растяжении нормальную силу принято считать положительной.

Правило знаков: при рассмотрении равновесия оставленной части стержня будем всегда предполагать нормальную силу N положительной, т. е. направленной от сечения, независимо от действия внешней нагрузки.

Проведем произвольные сечения на указанных участках MK, KC, CB и рассмотрим равновесие оставленных частей (рис. 2).


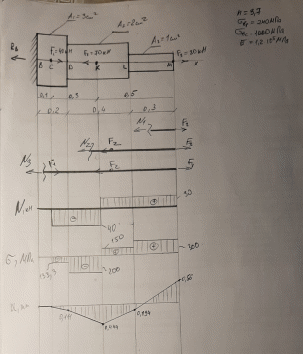
Рис. 2. Расчетная схема стержня и эпюры

Участок MK



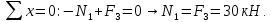
Знак плюс показывает

---

, что на участке МК действует растягивающая сила.
Участок KC



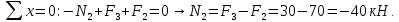
Знак плюс показывает, что на участке KC действует растягивающая сила.

Участок CB





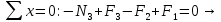
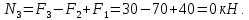
Реакция R_Bзаделки равна R_B= N₃ = 0 кН, что совпадает с результатом, полученным ранее из решения уравнения равновесия. Таким образом, если определять значения нормальных сил, оставляя каждый раз после проведения сечения левую часть стержня, то получим те же результаты.

Для построения эпюры N проведем ось абсцисс графика параллельно оси х стержня и отложим в произвольно выбранном масштабе значения нормальных сил по оси ординат y. Так как в пределах одного участка нормальная сила не меняется, то эпюра ограничена прямыми линиями, параллельными оси абсцисс (рис. 2). Полученные графики принято штриховать, при этом штриховка должна быть перпендикулярна оси стержня. Каждая линия штриховки в соответствующем масштабе выражает величину нормальной силы в лежащем против нее поперечном сечении.

Эпюра нормальных напряжений. При построении эпюры нормальных напряжений границами участков являются сечения, в которых приложены внешние сосредоточенные силы и изменяются размеры поперечного сечения. Следовательно, в этом случае имеем пять участков – ML, LK, KD, DC, CB (рис. 2). Напряжения для этих участков получим, разделив значения N на соответствующие площади поперечных сечений стержня, т.е. используем формулу:


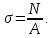
Участок ML



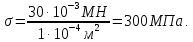
Участок LK



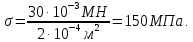
Участок KD



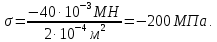
Участок DC



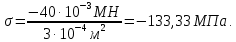
Участок CB



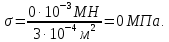
Эпюра перемещений. Эпюру перемещений следует строить, начиная от защемленного торца

---

В, для которого .

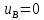Перемещение произвольного сечения, взятого в пределах участка BC на расстоянии х, равно удлинению части стержня длиной х (см. рис 2):



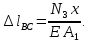
Полученное выражение показывает, что перемещения возрастают (по мере удаления сечения от заделки) по линейному закону. При нагружении стержня сосредоточенными силами в пределах каждого участка эпюра перемещений будет линейной; поэтому для ее построения достаточно определить перемещения сечений, совпадающих с границами участков.

Абсолютное перемещение сечения С (u_C) равно перемещению сечения В плюс удлинение участка BC, так как нормальная сила N₃ положительна:





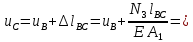
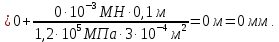
Абсолютное перемещение сечения D(u_D) равно перемещению сечения Cплюс удлинение участка CD, так как нормальная сила N₂ положительна:





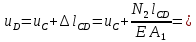
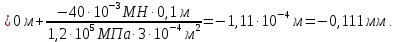
Абсолютное перемещение сечения K(u_K) равно перемещению сечения Dплюс удлинение участка DK, так как нормальная сила N₂ положительна:





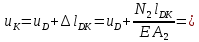
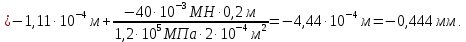
Абсолютное перемещение сечения L(u_L) равно перемещению сечения Kплюс удлинение участка KL, так как нормальная сила N₁ положительна:





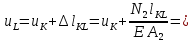
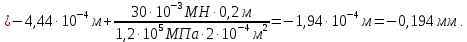
Абсолютное перемещение сечения M(u_M) равно перемещению сечения Lплюс удлинение участка LM, так как нормальная сила N₁ положительна:





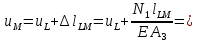
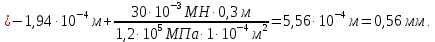
Построенная по полученным данным эпюра перемещений показана на рис. 2.

Вычисление перемещения свободного торца M

---

стержня на основе принципа независимости действия сил. На основе принципа независимости действия сил перемещение свободного торца u_Mстержня от нагрузок F₁, F₂ и F₃ равно сумме перемещений u_M (F₁), u_M (F₂), u_M (F₃) от действия каждой силы в отдельности, т.е.



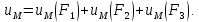
Вычисляем перемещения u_M (F₁), u_M (F₂), u_M (F₃), u_M .

Сила вызывает деформацию растяжения, поэтому в расчете ставим знак плюс: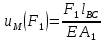





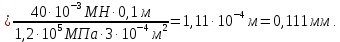
Сила вызывает деформацию сжатия, поэтому в расчете ставим знак минус: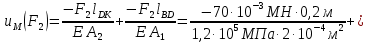





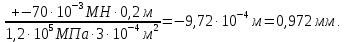
Сила вызывает деформацию растяжения, поэтому в расчете ставим знак плюс: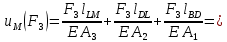







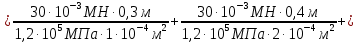
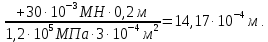
Следовательно,



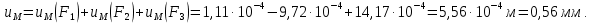
Полученный результат совпадает с результатом, полученным при построении полной эпюры перемещений (см. рис. 2).

Проверка прочности стержня. В связи с тем, что стержень изготовлен из материала, имеющего разные пределы прочности при растяжении и сжатии, проверку прочности необходимо отдельно проводить для участков, испытывающих растяжение и сжатие. При этом выделяются участки, имеющие наибольшие растягивающие и сжимающие напряжения (рис. 2, эпюра σ).

Участок LM – .

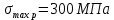Вычисляем допускаемые напряжения при растяжении:

---

Смотрите также файлы

• Предметные требования с овз прописывались по каждому предмету дополнительным блоком.docx

• Обжиг глины был уже в специальной, а не на обычном очаге.docx

• Анализ фильма (сериала) по дисциплине Социология Выполнили студенты группы.docx

• Центр помощи Аддиктивные и суицидальные формы поведения.pptx

• Влияние физических упражнений на основные системы организма.docx