Файл: Урок Прямая и отрезок.docx

Ресурсный материал

Игра

Теоретические вопросы.

1. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.

2. Что такое градусная мера угла?

3. Какой угол называется развернутым?

4. Луч ОС делит угол АОВ на два угла. Как найти градусную меру угла АОВ, если известны градусные меры углов АОС и СОВ?

5. Сколько прямых можно провести через две прямые точки?

6. Объясните, как сравнить два угла.

7. Какие фигуры называются равными?

8. Какой угол называется острым? прямым? тупым?

9. Сколько общих точек могут иметь две прямые?

10. Какой луч называется биссектрисой угла?

11. Объясните, как сравнить два отрезка.

12. Какие углы называются смежными? Чему равна сумма смежных углов?

13. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы?

14. Какие приборы применяют для построения прямых углов на местности?

15. Какая точка называется серединой отрезка?

16. Какие прямые называются перпендикулярными?

17. Объясните, что такое луч. Как обозначаются лучи?

18. Какими инструментами пользуются для измерения расстояний?

Задачи.

1. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 220°.

2. На прямой b отмечены точки С, D и Е, причем СD = 6 см, DЕ = 8 см. Какой может быть длина отрезка СЕ?

3. Три точки В, D и С лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?

4. Один из смежных углов на 28° меньше другого. Найдите оба смежных угла.

5. Начертите угол 132° и проведите биссектрису смежного с ним угла.

6. Точка М – середина отрезка АВ, МВ = 4,3 дм. Найдите длину отрезка АВ.

7. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 300°.

8. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.

9. Три точки М, N и K лежат на одной прямой. Известно, что МN = 15 см, NK = 18 см. Каким может быть расстояние МK?

10. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.

11. Один из смежных углов в 11 раз больше другого. Найдите оба смежных угла.

12. Один из смежных углов в 8 раз больше другого. Найдите оба смежных угла.

13. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.

---

14. Точка М – середина отрезка АВ, МВ = 2,5 см. Найдите длину отрезка АВ.

15. Один из смежных углов равен 52°. Найдите другой угол.

16. Один из вертикальных углов, образованный при пересечении двух прямых, равен 35°. Найдите другие неразвернутые углы.

17. Точки А, В, М лежат на одной прямой. Длина отрезка АВ = 7,3 см, АМ = 3 см. Какой может быть длина отрезка МВ?

18. ОС – биссектриса угла АОВ. Известно, что угол АОС равен 43°. Найдите градусную меру угла АОВ.

Урок62. Повторение. Признаки равенства треугольников.
Равнобедренный треугольник

Цели деятельности учителя	Создать условия для систематизации знаний, умений, навыков учащихся по данной теме; совершенствовать навыки решения задач по теме «Признаки равенства треугольников. Равнобедренный треугольник»
Термины и понятия	Признаки равенства треугольников, боковая сторона, основание, медиана, биссектриса, высота, углы при основании
Планируемые результаты
Предметные умения		Универсальные учебные действия
Применяют изученные понятия, результаты, методы для решения задач практического характера		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: осознают важность и необходимость изучения предмета
Организация пространства
Формы работы	Фронтальная (Ф); парная (П); индивидуальная (И)
Образовательные ресурсы	• Задания для фронтальной (парной) работы. • Тест

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Устранить пробелы в знаниях учащихся	(Ф/И) Заслушать сочинения учащихся
II этап. Тест
Цель деятельности	Совместная деятельность
Систематизировать теоретические знания учащихся	(И) Учащиеся выполняют тестовые задания (см. Ресурсный материал)
III этап. Решение задач по готовым чертежам
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения задач	(Ф/И/П) Записать короткое решение к задачам по готовым чертежам. 1) Доказать: DB – биссектриса ADC. 2) Доказать: О – середина АВ. 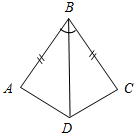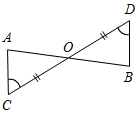Рис. 1 Рис. 2 3) Дано: С – середина АЕ, ВС + CD = 10 см. 4) Доказать: ВС = DC. Найти: ВС. 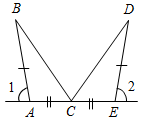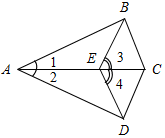Рис. 3 Рис. 4 5) Доказать: ВЕ = АС, ED = DC. 6) Найти:BFC. 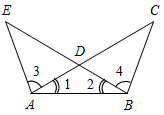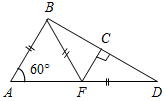Рис. 5 Рис. 6 7) Найти:AFD. 8) Найти:BAC. 9) Найти: АВ. 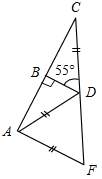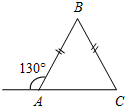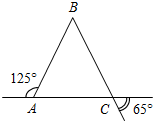Рис. 7 Рис. 8 Рис. 9
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
– Уточните алгоритм исправления ошибок. – Назовите способы действий, вызвавшие затруднение. – Оцените собственную деятельность на уроке		(И) Домашнее задание: повторить главу III, вопросы 1–15; решить оставшиеся задачи. Дополнительные задачи: № 328–332 на выбор учащихся

---

Ресурсный материал

Тест

1. Для доказательства равенства ∆АВС и ∆DEF (рис. 1) достаточно доказать, что:

а) AB = DF; б) AC = DE; в) AB = DE.

2. Для доказательства равенства ∆АВС и ∆EDF (рис. 2) достаточно доказать, что:

a) A = D; б)B = D; в)A = E.



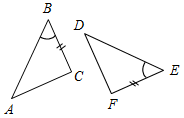
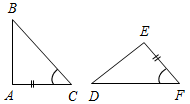
Рис. 1 Рис. 2

3. Из равенства ∆АВС и ∆FDE (рис. 3) следует, что:

a) AB = FD; б) AC = DF; в) AB = EF.

4. Из равенства ∆АВС и ∆DEF (рис. 4) следует, что:

a) B = D; б) A = E; в) C = F.



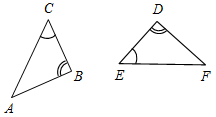
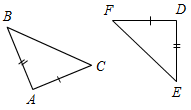
Рис. 3 Рис. 4

5. В ∆ABC все стороны равны, и в ∆DEF все стороны равны. Чтобы доказать равенство ∆АВС и ∆DEF, достаточно доказать, что:

a) В = D; б) AB = DE; в) Р_АВС = P_DEF.

6. «Медиана в равнобедренном треугольнике является биссектрисой и высотой». Это утверждение:

а) всегда верно; б) всегда неверно; в) может быть верно.

7. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?

а) в любом; б) равнобедренном; в) равностороннем.

8. Если в треугольнике два угла равны, то этот треугольник:

а) равнобедренный; б) равносторонний; в) прямоугольный.

9. Если треугольник равносторонний, то:

а) он равнобедренный; б) все его углы равны; в) любая его биссектриса является его медианой и высотой.

Ответы: 1 – в; 2 – в; 3 – а; 4 – в; 5 – б, в; 6 – в; 7 – б; 8 – а; 9 – а, б, в.

Урок63. Повторение. Признаки равенства треугольников.
Равнобедренный треугольник

Цели деятельности учителя	Создать условия для систематизации знаний, умений, навыков учащихся по данной теме; совершенствовать навыки решения задач по теме «Признаки равенства треугольников. Равнобедренный треугольник»
Термины и понятия	Признаки равенства треугольников, боковая сторона, основание, медиана, биссектриса, высота, углы при основании
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, результаты, методы для решения задач практического характера		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в группе, в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для теста. • Задания для групповой и домашней работы

---

I этап. Тестовые задания
Цель деятельности	Совместная деятельность
Повторить теоретические сведения	(И) Блицтест (10 мин). Тест сдается на проверку учителю. Задание № 1 (оценивается в 4 балла). Отрезки MN и KB пересекаются в точке А. Точка А является серединой этих отрезков. Докажите, что треугольники MKA и NBA равны (рис. 1). 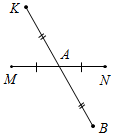Рис. 1 Задание № 2 (оценивается в 6 баллов). Луч АВ – биссектриса угла АОЕ, перпендикулярен отрезку ОЕ. Найдите длину отрезка АО, если АЕ = 5 см
II этап. Решение задач
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения задач	(Г) Класс разбивается на 4 группы. Учащиеся 15 минут работают в группах, затем представляют свои решения, обсуждают задачи. 1) На рисунке 2 ВЕ и СF – высоты ∆АВС. При помощи только линейки постройте высоту АХ этого треугольника. Найдите длину ВС, если АХ = ВЕ, СХ = СЕ, АС = 17 дм. 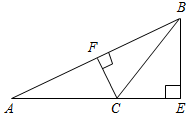Рис. 2 2) На рисунке 3 ∆АВС – равнобедренный, L – середина АС, АМ = СK. Доказать, что ML = LK. 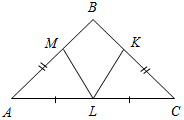Рис. 3 3) На рисунке 4 НKN = MNK, KО = ОN. Доказать, что KHN = KMN. 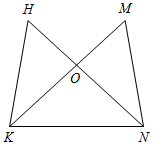Рис. 4
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какие свойства равнобедренного треугольника повторили? – Оцените свою работу и работу группы		(И) Домашнее задание: решить тест. Каждое из заданий № 1, 2 оценивается в 4 балла. 1. Укажите номера верных утверждений. 1) Высота треугольника всегда лежит внутри треугольника. 2) Медиана – это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. 3) В равнобедренном треугольнике медиана совпадает с биссектрисой, проведенной из той же вершины. 4) В равностороннем треугольнике все углы равны. 2. Докажите, что биссектриса равностороннего треугольника разбивает его на два равных треугольника

---