Файл: Урок Прямая и отрезок.docx

Урок3. Сравнение отрезков и углов

Цель деятельности учителя	Создать условия для введения одного из важнейших геометрических понятий – понятия равенства фигур, в частности равенства отрезков и углов; для обучения учащихся сравнению отрезков и углов, введения понятий середины отрезка и биссектрисы угла
Термины и понятия	Отрезок, прямая, точка, плоскость, луч, угол, биссектриса угла, середина отрезка
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления		Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют находить в различных источниках информацию, необходимую для решения математических проблем. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для самостоятельной работы

I этап. Актуализация опорных знаний. Вводное повторение
Цель деятельности	Совместная деятельность
Систематизировать теоретический материал	(Ф) Вопросы к учащимся: 1) Назовите основные геометрические фигуры на плоскости. 2) Что такое планиметрия? 3) Как можно обозначить прямую? 4) Что называется отрезком? 5) Сколько общих точек могут иметь две прямые? 6) Сколько прямых можно провести через любые две точки плоскости? 7) Объясните, что такое луч. Как обозначаются лучи? 8) Какая фигура называется углом? Объясните, что такое вершина и стороны угла. 9) Какой угол называется развернутым? 10) Сколько неразвернутых углов образуется при пересечении трех прямых, проходящих через одну точку? (Двенадцать углов.)
II этап. Изучение нового материала
Цель деятельности	Совместная деятельность
Ввести понятие биссектрисы угла	(Ф) Введение понятия равенства фигур. Вывод: две геометрические фигуры называются равными, если их можно совместить наложением. 1) Сравнение фигур. – Задача сравнения фигур (их форм и размеров) является одной из основных в геометрии. На практике сравнить наложением две небольшие плоские фигуры вполне возможно, а вот два очень больших стекла, а тем более два земельных участка практически невозможно. Это приводит к выводу о необходимости определенных правил сравнения двух фигур, позволяющих сравнить некоторые их размеры и по результатам этого сравнения сделать вывод о равенстве или неравенстве данных фигур. (Можно предложить учащимся сравнить некоторые фигуры наложением кальки.) 2) Работа по рис. 20 учебника. Запись в тетрадях: ВK = DМ (равные отрезки); АС <АВ. 3) Введение понятия середины отрезка (рис. 21). 4) Решение задач № 19 и 20 (по рис. 25). 5) Работа по рис. 22 и 23 учебника. 6) Выполнение задания № 21 на доске и в тетрадях. 7) Введение понятия биссектрисы угла (рис. 24). 8) Решение задачи № 22 (устно)
III этап. Решение задач
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения задач	(Ф/И) 1. Самостоятельная работа в форме диктанта. 1) На луче h с началом в точке О отложите отрезки ОА и ОВ так, чтобы точка А лежала между точками О и В. Сравните отрезки ОА и ОВ и запишите результат сравнения. 2) Начертите неразвернутый угол АВС и проведите произвольный луч ВD, делящий этот угол на два угла. Сравните углы АВС и АВD, АВС и DВС и запишите результаты сравнения. 2. Решение задач. № 1. На прямой а от точки А отложены два отрезка АВ и АС, причем АВ<АС< 1,99АВ. Сравните отрезки ВС и АВ (рис. 1а). АС < 1,99АВ, АС < АВ +0,99АВ, тогда ВС < 0,99АВ, следовательно, ВС <АВ; (рис. 1б) АВ – частьВС, поэтому ВС < АВ. а) Рис. 1 б) № 2. AOC = BOD, ОМ и ON – биссектрисы углов АОВ и COD. Сравните углы MON и АОС. (AOB = COD, так как AOC = BOD, a ВОС – общая часть углов АОС и BOD. Так как ОМ и ON – биссектрисы углов АОВ и COD(по усл.), следовательно,АОМ = МОВ = CON = NOD. AOC = АОМ + МОВ + ВОС, MON = МОВ + ВОС + CONMON = AOC.) 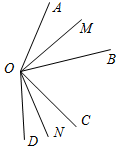Рис. 2
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какие фигуры называются равными? – Что такое биссектриса угла? – Задайте три вопроса по теме		(И) Домашнее задание: изучить пункты 5 и 6 из § 3; ответить на вопросы 7–11 на с. 25; решить задачи № 18 и 23

1   2   3   4   5   6   7   8   9   ...   47

---

Урок 4. Измерение отрезков

Цель деятельности учителя		Создать условия для ознакомления учащихся с процедурой измерения отрезков, введения понятия длины отрезка и рассмотрения свойств длин отрезков, ознакомления с различными единицами измерения и инструментами для измерения отрезков
Термины и понятия		Отрезок, прямая, точка, середина отрезка
Планируемые результаты
Предметные умения			Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления			Познавательные: владеют первоначальными сведениями об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: имеют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для фронтальной и самостоятельной работы
I этап. Актуализация опорных знаний
Цель деятельности	Совместная деятельность
Выявить трудности, возникшие при выполнении домашнего задания	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Проверить правильность решения домашней работы. Для этого вызвать к доске троих учащихся
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Способствовать изучению новой темы, используя текст учебника	(Ф/И) Учащимся предлагается прочитать самостоятельно § 4 «Измерение отрезков» и ответить на вопросы,записанные на доске. – Какие основные единицы измерения длины нам известны? А дополнительные? (Основные единицы измерения длины отрезка: мм, см, дм, м, км; дополнительные единицы измерения длины отрезка: световой год (путь, который проходит свет в течение одного года), морская миля (1,852 км); старинные единицы измерения длины: аршин (0,7112 м), сажень (2,1336 м), косая сажень (2,48 м), маховая сажень (1,76 м), локоть (0,45 м) и другие.) – Как найти длину отрезка, если точка делит его на два отрезка, длины которых известны? (Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков.) – Какими инструментами пользуются для измерения расстояний? (Для измерения расстояний используются масштабная миллиметровая линейка, штангенциркуль, рулетка.)
III этап. Решение задач
Цель деятельности	Деятельность учителя				Деятельность учащихся
Закрепить полученные знания	(Ф/И) Учитель показывает оформление решения задачи на доске, объясняя, как из условия задачи выделить, что дано и что требуется найти или доказать. 1. Решить задачу № 32 (письменно; один ученик у доски, остальные – в тетрадях). 2. Решить задачи № 30, 31 (б) на доске и в тетрадях. 3. Выполнить задания и сделать необходимые краткие записи на доске и в тетрадях. 1) Дан луч h с началом в точке О; Вh, Аh; точка В лежит между точками О и А. а) Какой из отрезков: ОВ или ОА – имеет бо́льшую длину? б) Найдите АВ, если ОА = 72 см, ОВ = 4,2 дм. 2) Начертите прямую а и отметьте точку А, не лежащую на этой прямой. С помощью масштабной линейки и циркуля отметьте на прямой а точку D, удаленную от точки А на расстояние 3 см. (Выяснить вместе с учащимися, что задача может иметь одно или два решения, а может и не иметь решений.) 4. Решить задачу № 29 учебника. 5. Выполнить задание. Начертите отрезок СD, равный 5 см. С помощью масштабной линейки отметьте на прямой СD точку В, такую, что СВ = 2 см. а) Сколько таких точек можно отметить на прямой СD? б) Какова длина отрезка ВD? Рассмотрите все возможные случаи				(И) № 32. Дано: А, В, Са, АВ = 12 см, ВС = 13,5 см. Найти: АС. Решение: На прямой а отметим точки А, В, С. Возможны случаи: а) Точка В лежит между точками А и С, тогда АС = АВ + ВС, АС = 12 см + 13,5 см = 25,5 см. б) Точка А лежит между точками В и С, тогда АС = СВ – АВ, АС = 13,5 см – 12 см = 1,5 см. в) Точка С не может лежать между точками А и В, так как АВ<ВС. 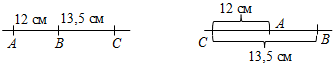а) б) Ответ: 25,5 см или 1,5 см
IV этап. Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень сформированности теоретических знаний и практических навыков	(И) Решить задачи № 28, 27, 31, 34 из учебника. Дополнительные задачи для тех, кто справился с работой. № 1. Длина отрезка АВ равна 14 см. Найдите на прямой все такие точки D, для которых DA = 3DB. Ответ: если DАВ, то AD = 10,5 см, DB = 3,5 см; если ВАD, то DB = 7 см, AD = 21 см. № 2. Точки А, В и С лежат на одной прямой, причем длина отрезка ВС больше длины отрезка АС в 3 раза, а длина АВ меньше длины ВС на 3,6 см. Найдите длину отрезка АС. Ответ: АС = 3,6 см
IV этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Как измерить отрезки и сравнить их? – Составьте синквейн к уроку				(И) Домашнее задание: изучить пункты 7, 8 из § 4; ответить на вопросы 12 и 13, с. 25; решить задачи № 24, 25, 28, 33, 36 (решение задачи приведено в учебнике)

---

Урок5. Решение задач по теме «Измерение отрезков»

Цели деятельности учителя	Создать условия для обучения учащихся решению задач на нахождение длины части отрезка или всего отрезка; способствовать развитию логического мышления
Термины и понятия	Отрезок, прямая, точка, середина отрезка
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления		Познавательные: имеют первоначальные сведения об идеях и о методах математики как универсального языка науки и техники, о средствах моделирования явлений и процессов. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Чертежи к задачам. • Задания для самостоятельной работы

I этап. Актуализация опорных знаний
Цель деятельности	Совместная деятельность
Выявить трудности, возникшие при выполнении домашнего задания	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Проверить правильность выполнения домашнего задания
II этап. Решение задач
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения задач	(Ф/И) 1. Решить задачи по рисункам (устно;рисунки подготовлены на доске заранее). а) Дано: ВС = 2,5 см. б) Дано: AD = 42 см, ВС = 11 см. в) Дано: АВ : АС = 4 : 5; АС = 12,5 дм. Найти: АС. Найти: АВ. Найти: АВ. Рис. 1 Рис. 2 Рис. 3 Ответ: АС = 5 см. Ответ: АВ = 20 см. Ответ: АВ = 10 дм. 2. Решить задачи № 38, 40 (письменно). № 38. Дано: О, А, В лежат на одной прямой, ОА = 12 см, ОВ = 9 см. Найти: расстояние между серединами отрезков ОА и ОВ. Решение: Пусть М – середина отрезка ОА, N – середина отрезка ОВ. Возможны два случая: а) Рис. 4 б) а) Если точка О лежит на отрезке АВ, то МО = АО : 2 = 6 см, NО = ВО : 2 = 4,5 см. Расстояние между серединами отрезков ОА и ОВ равно длине отрезка MN, a MN = МО + ON = 6 см + 4,5 см = 10,5 см. б) Если точка О не лежит на отрезке АВ, то МО = АО : 2 = 6 см, NО = ВО : 2 = 4,5 см, MN = МО – ON = = 6 см – 4,5 см = 1,5 см. Ответ: а) 10,5 см; б) 1,5 см. № 40 (предложить учащимся решить самостоятельно, а затем проверить решение задачи). Дано: АВ = 28 см; С, DАВ; М – середина AC; N – середина DB; MN = 16 см. Найти: CD. Рис. 5 Решение: АВ = AM + MN + NB; АМ + NB = AB – MN = 28 см – 16 см = 12 см. М – середина АС, значит, АМ = MС; N – середина BD, значит, BN = ND. Так как АМ + NB = 12 см, АМ = МС, BN = ND, то MC + DN = 12 см. MN = МС + CD + DN = 16 см, МС + DN = 12 см, значит, CD = MN – (MC + DN) = 16 см – 12 см = 4 см. Ответ: 4 см
III этап. Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень сформированности знаний учащихся	(И) Работа выполняется на листочках и сдается на проверку учителю. Вариант I 1. На отрезке АВ взяты точки С и D. Найдите длину отрезка CD, если АВ = 12 см, АС = 3 см, BD = 4 см. 2. На отрезке АВ длиной 36 см взята точка K. Найдите длину отрезков АK и ВK, если АK больше ВK на 4 см. 3. На прямой отмечены точки А, В, С так, что АВ = 27 м, АС = 11 м, ВС = 16 м. Какая из этих точек лежит между двумя другими? Вариант II 1. На отрезке АВ взята точка С, а на отрезке СВ – точка D. Найдите длину отрезка BD, если АВ = 15 см, CD = 7 см, АС = 6 см. 2. На отрезке АВ длиной 36 см взята точка K. Найдите длину отрезков АK и ВK, если АK больше ВK в 3 раза. 3. На прямой отмечены точки А, В, С так, что АВ = 7 м, АС = 21 м, ВС = 28 м. Какая из этих точек лежит между двумя другими?
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Оцените свою работу на уроке. – Какие задания вызвали у вас наибольшие затруднения?		(И) Домашнее задание: решить задачи № 35, 37, 39

1   2   3   4   5   6   7   8   9   ...   47

---

Урок6. Измерение углов

Цель деятельности учителя	Создать условия для введения понятия градусной меры угла и рассмотрения свойств градусных мер углов, введения понятий острого, прямого и тупого углов, ознакомления учащихся с приборами для измерения углов на местности
Термины и понятия	Градус, минута, секунда, угол
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления		Познавательные: выдвигают гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); коллективная (К)
Образовательные ресурсы	• Задания для самостоятельной и фронтальной работы. • Вопросы для викторины

I этап. Актуализация опорных знаний
Цель деятельности	Задания для самостоятельной работы
Систематизировать теоретические знания	(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Самостоятельная работа на 10 минут с взаимопроверкой. Вариант I 1. На прямой b отмечены точки С, D и Е так, что СD = 6 см, DЕ = 8 см. Какой может быть длина отрезка СЕ? Ответ: СЕ = 14 см или СЕ = 2 см. 2. Точка М – середина отрезка АВ; МВ = 4,3 дм. Найдите длину отрезка АВ в миллиметрах. Вариант II 1. На прямой m отмечены точки А, В и С так, что АС = 12 см, АВ = 8 см. Какой может быть длина отрезка ВС? Ответ: ВС = 20 см или ВС = 4 см. 2. Точка Р – середина отрезка MN. Найдите длину отрезка PN в метрах, если MN = 14 дм
II этап. Изучение нового материала. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Ввести понятия единиц измерения углов (градус, минута, секунда)	(Ф/К) 1. Понятия градуса, градусной меры угла, развернутого и прямого углов были введены еще в 5 классе. Возможно, учащиеся знакомы также с острыми и тупыми углами. Поэтому можно предложить ученикам викторину, а в случае затруднения ответы на вопросы викторины порекомендовать найти в пункте 9 и записать их в тетрадях. Викторина: 1) Единица измерения углов. (Градус.) 2) Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле. (Градусная мера угла.) 3) часть развернутого угла. (Градус.) 4) часть градуса. (Минута.) 5) часть минуты. (Секунда.) 6) Градусная мера развернутого угла. (180°.) 7) Градусная мера прямого угла. (90°.) 8) Градусная мера неразвернутого угла. (Меньше 180°.) 9) Угол, градусная мера которого меньше 90°. (Острый.) 10) Угол, градусная мера которого больше 90°, но меньше 180°. (Тупой.) После того, как проверены ответы на вопросы викторины, можно перейти к рассмотрению свойств: • Равные углы имеют равные градусные меры. • Меньший угол имеет меньшую градусную меру. • Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов (рис. 34 учебника на с. 19). 2. Выполнение практических заданий № 41, 42, 43. 3. Решение задач № 45, 46 (устно). 4. Введение понятий прямого, острого и тупого углов с помощью рис. 35. 5. Решение задач № 51 (по рис. 38), 52 (по рис. 39) и 53 (устно)
III этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения задач	(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 47 и 48. Решение записывается на доске и в тетрадях (объясняет учитель). 2. Решить задачи обучающего характера на доске и в тетрадях (учащиеся с помощью учителя делают на доске чертеж, записывают, что дано и что нужно найти, учатся оформлять решение задачи): 1) Луч ВD делит развернутый угол АВС на два угла, разность градусных мер которых равна 46°. Найдите образовавшиеся углы. 2) Луч СК делит прямой угол ВСМ на два угла, один из которых в 4 раза больше другого. Найдите образовавшиеся углы. 3) Луч DО делит прямой угол АDВ на два угла, градусные меры которых относятся как 5 : 4. Найдите угол между лучом DО и биссектрисой угла АDВ		№ 47. Дано:АОВ. а) АОЕ = 44°, ЕОВ = 77°. б) АОЕ = 12°37, ЕОВ = 108°25. Найти:АОВ. 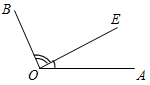Рис. 1 Решение: а) АОВ = АОЕ + ЕОВ(свойство измерения углов). АОВ = 44° + 77° АОВ = 121° б) АОВ = АОЕ + ЕОВ АОВ = 12°37 + 108°25 АОВ = 120°62 = 121°02, так как 60 = 1°. Ответ: а) 121°; б) 121°02. № 48. Дано:АОВ = 78°, АОС меньше ВОС на 18°. Найти:СОВ. 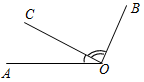Рис. 2 Решение: Примем АОС = х, следовательно, СОВ = х + 18. Так как АОВ = АОС + СОВ, то: 78 = х + х + 18 78 = 2х + 18 2х = 60 АОС = 30°, СОВ = 48°. Ответ: 48°
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Составьте четверостишие с использованием слов «угол», «биссектриса», «градус», «развернутый угол», «прямой угол»		(И) Домашнее задание: изучить пункты 9 и 10 (самостоятельно); ответить на вопросы 14–16 на с. 25–26; выполнить практическое задание № 44; решить задачи № 49, 50, 52

---

Урок7. Смежные и вертикальные углы

Цель деятельности учителя	Создать условия для введения понятий смежных и вертикальных углов, рассмотрения их свойств, введения понятия перпендикулярных прямых и демонстрации применения этих понятий при решении задач
Термины и понятия	Угол, смежные углы, вертикальные углы, перпендикулярные прямые
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления		Познавательные: выдвигают гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); парная (П)
Образовательные ресурсы	• Задания для самостоятельной работы

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Задания для самостоятельной работы
Систематизировать теоретические знания	(И) Самостоятельная тестовая работа с последующей самопроверкой (см. Ресурсный материал)
II этап. Изучение нового материала
Цель деятельности	Совместная деятельность
Ввести понятия смежных углов, вертикальных углов и перпендикулярных прямых	(Ф) 1. Ввести понятие смежных углов и ознакомить учащихся с их свойством: сумма смежных углов равна 180°. 2. Выполнить практическое задание № 55 (на доске и в тетрадях). 3. Решить задачи № 58, 59, 60, 63, 62 (по рис. 46 на с. 24) (устно). 4. Решить задачу № 61 (в, г) (письменно). Решение записывает на доске учитель. 5. Понятие вертикальных углов можно ввести во время выполнения следующего задания: – Начертите неразвернутый АОВ и назовите лучи, являющиеся сторонами этого угла. – Проведите луч ОС, являющийся продолжением луча ОА, и луч ОD, являющийся продолжением луча ОВ. – Запишите в тетради: углы АОВ и СОD называются вертикальными. 6. Дать определение вертикальных углов (рис. 41 на с. 22). 7. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере, который фиксируется на доске и в тетрадях учащихся. Доказательство: МОK + DOM = 180°, так как МОK и DOM смежные и их сумма равна 180°, отсюда МOK = = 180° – DOM. COD + DOM = 180°, так как COD и DОM смежные и их сумма равна 180°, отсюда COD = = 180° – DOM. 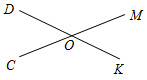Рис. 1 Получили, что МОK = 180° – DОM и COD = 180° – DOM, значит, MOK = COD, а это вертикальные углы. Итак, вертикальные углы равны. 8. Решить задачу № 65 (устно). 9. Решить задачу № 67 по рис. 47 на с. 25 (устно). 10. Ввести понятие перпендикулярных прямых (рис. 42 на с. 22). 11. Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые. 12. Выполнить практическое задание № 57. 13. Провести беседу о построении прямых углов на местности (п. 13)
III этап. Решение задач
Цель деятельности	Совместная деятельность
Отработать основные понятия при решении задач	(Ф/И) Решить на доске и в тетрадях № 65 (а), 66 (а). (П) Решить № 64 (а), 66 (б), представить решение на доске и обсудить
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Оцените свою работу в парах и поставьте друг другу оценки. – Составьте синквейн к уроку		(И) Домашнее задание: изучить пункты 11–13 из § 6; ответить на вопросы 17–21 на с. 26; выполнить практическое задание № 56; решить задачи № 61 (а, б), 66 (в), 68; повторить весь изученный материал и подготовиться к контрольной работе, просмотрев по тетрадям решение задач

---