Файл: Урок Прямая и отрезок.docx

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Привести в систему знания по теме	(Ф/И) Проверить правильность выполнения домашнего задания. № 335. Решение: а) В АВС по условию А + В> 90°, а так как А + В + С = 180°, то С< 90°. Так же можно получить, что А< 90°, В< 90°, то есть АВС – остроугольный. б) В АВС по условию А<В + С, а так как В + С = 180° – А, то А< 180° – А, А< 90°. Аналогично можно получить, что В< 90°, С < 90°, тогда АВС – остроугольный 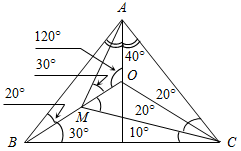Рис. 1
II этап. Решение по готовым чертежам
Цель деятельности	Совместная деятельность
Проверить умение применять теоретические знания в решении задач	(П) Рисунки начертить в тетрадях и на них записать промежуточные результаты. Записать ответы. 1. Дано:С = 50°, А на 20° больше В. 2. Дано:A : B : C = 11 : 4 : 3. Найти:A, B. Найти:A, B, C. 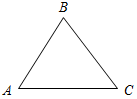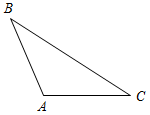Рис. 2 Рис. 3 Ответ: A = 15°, B = 55°. Ответ:A = 110°, B = 40°, C = 30°. 3. Дано:A в 1,5 раза меньше В. 4. Найти: A, C. Найти:A, В. 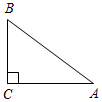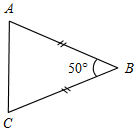Рис. 4 Рис. 5 Ответ: A = 36°, B = 54°. Ответ: A = 65°, C = 65°. 5. Найти:ACD. 6. Найти:B. 7. Найти: АС. 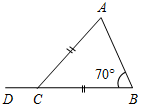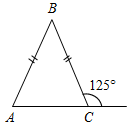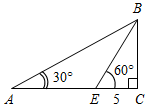Рис. 6 Рис. 7 Рис. 8 Ответ:ACD = 140°. Ответ: B = 70°. Ответ: АС = 15. 8. Найти: АВ. 9. Дано: СЕ – биссектриса. 10. Дано: АВ = ВС. Найти:A, B. Найти:B. 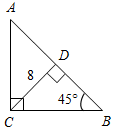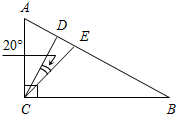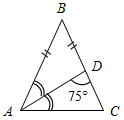Рис. 9 Рис. 10 Рис. 11 Ответ: АВ = 16. Ответ: A = 65°, B = 25°. Ответ: B = 40°. 11. Найти:DFE. 12. Найти:BAD. 13. Дано: СЕ – медиана. Найти:A, В. 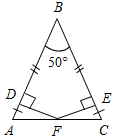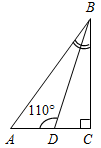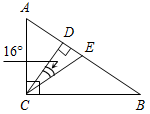Рис. 12 Рис. 13 Рис. 14 Ответ:DFE = 130°. Ответ:BAD = 50°. Ответ: A = 53°, В = 37°. 14. Найти:В. 15. Найти:АВС. 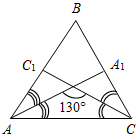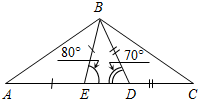Рис. 15 Рис. 16 Ответ: B = 80°. Ответ: АВС = 135°
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Оцените свою работу и работу своего соседа по парте. – Какие трудности возникли при решении задач?		(И) Домашнее задание: повторить § 4 (глава IV); прочитать тему «Задачи на построение» на с. 95 учебника

---

Урок68. Повторение. Задачи на построение

Цель деятельности учителя	Создать условия для повторения основных задач на построение; совершенствовать навыки решения задач на построение
Термины и понятия	Построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, середины отрезка
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, результаты, методы для решения задач практического характера		Познавательные: умеют планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для индивидуальной работы

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Повторить основные задачи на построение	(Ф/И) 1. Шесть учеников выполняют у доски следующие задания: 1) на данном луче от его начала отложить отрезок, равный данному; 2) отложить от данного луча угол, равный данному; 3) построить биссектрису данного неразвернутого угла; 4) построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка; 5) построить середину данного отрезка; 6) построить прямую, проходящую через данную точку и перпендикулярную к прямой, не проходящей через данную точку. 2. Пока учащиеся у доски готовятся, класс выполняет дифференцированные задания. Построить треугольник: 1) по двум сторонам и углу между ними; 2) по стороне и прилежащим к ней углам; 3) по трем сторонам
II этап. Решение задач
Цель деятельности	Деятельность учителя	Деятельность учащихся
Совершенствовать навыки решения задач на построение	(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 353 на доске и в тетрадях. 2. Решить самостоятельно задачи № 354, 360, 362 (одну задачу решить по полной схеме)	№ 353. Анализ(см. рис.1): 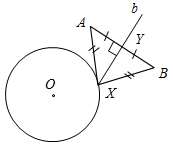Рис. 1 Пусть X – искомая точка, то есть АХ = ХВ, тогда ∆АХВ – равнобедренный и XY – медиана, высота и биссектриса. Отсюда получаем план построения. План построения: 1) Построить точку Y – середину АВ. 2) Построить прямую, проходящую через Y и перпендикулярную АВ. 3) Прямая b пересекается с окружностью в точках Х и Z. Х и Z – искомые точки. Построение(см. рис. 2): 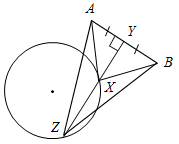Рис. 2 Доказательство: ∆AYX = ∆BYX по двум катетам (они прямоугольные, так как YXАВ, AY = YB, так как Y – середина АВ), тогда АХ = ВХ, то есть точка Х лежит на данной окружности и равноудалена от концов отрезка АВ. Таким же образом можно доказать, что точка Z удовлетворяет всем условиям задачи. Исследование: Задача может иметь: а) два решения (см. план построения и построение); б) одно решение, если прямая b имеет одну общую точку с окружностью (касается ее) (рис. 3); в) ни одного решения, если прямая b не имеет общих точек с окружностью (рис. 4). 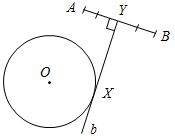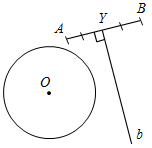Рис. 3 Рис. 4 № 354. Соединяем точки А, В и С. Находим середины отрезков АВ, ВС и АС, соответственно K, L и М. Проводим перпендикуляры (серединные перпендикуляры АВС). Находим точку О – их точку пересечения. Проводим окружность радиуса АО = = ВО = СО с центром в точке О. Вокруг треугольника всегда можно описывать окружность, поэтому задача не имеет решения, лишь когда точки лежат на одной прямой. 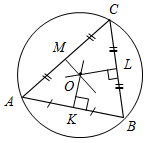Рис. 5 № 360. 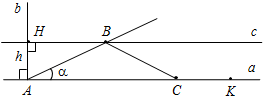Рис. 6 Проводим прямую а. Отмечаем на ней точку А – одну из вершин нашего треугольника, на прямой откладываем отрезок, равный периметру треугольника. На прямой b откладываем отрезок АН, равный высоте треугольника. Строим заданный  с вершиной в точке А. Проводим прямую сb, Нс. Обозначим точку пересечения с со стороной  – В. От точки K откладываем на прямой а отрезок, равный АВ – KC. Соединяем В и С. АВС – искомый треугольник. № 362. 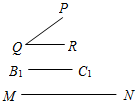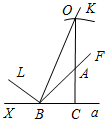а) Рис. 7 б) Пусть надо построить АВС, и даны PQR и отрезки В1С1, равный стороне треугольника, и MN, равный сумме двух других сторон треугольника (см. рис. а). Проведем произвольную прямую а, отметим на ней точку В и точку Х(см. рис. б). От луча ВХ отложим угол XBL, равный углу PQR(см. пункт 23 учебника). От точки В отложим отрезок, равный данному отрезку В1С1. Построим биссектрису BK угла LBC(см. пункт 23 учебника). Построим окружность С радиусом, равным MN, и центром С, она пересечет луч BK в точке О. Отложим от луча BKKBF, равный углу BKC. Луч BF пересечет СО в точке А. Треугольник АВС – искомый, докажем это. KAB = АВС + АСВ (как внешний). KAB – равнобедренный (так как BKA = KBA по построению). Значит, KBA = . KBС = KBA + АВС = + АВС = . LBC = 2KBС = 180° + АВС – АСВ (так как BK – биссектриса угла LBC). PQR = XBL = 180° – LBC = 180° – 180° – АВС + АСВ = АСВ – АВС. АВ = AK, так как KBA – равнобедренный, значит, MN = KA + АС = АВ + АС, следовательно, наши построения верны
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какой этап в задачах на построение у вас вызывает наибольшее затруднение? – Оцените свою работу на уроке		(И) Домашнее задание: решить задачи № 352, 356, 361 (одну задачу решить по полной схеме)

---

Уроки69–70. Итоговый контрольный тест

Цели деятельности учителя	Создать условия для приведения в систему знаний, умений, навыков за курс геометрии 7 класса; совершенствовать навыки решения задач
Термины и понятия	Углы, равнобедренный треугольник, прямоугольный треугольник, высота, медиана, биссектриса, параллельные прямые
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, методы для решения задач практического характера		Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость знаний в жизни человека
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для теста

I этап. Актуализация опорных знаний
Цель деятельности	Совместная деятельность
Проверить правильность выполнения домашней работы	(Ф/И) Ответить на вопросы по домашнему заданию
II этап. Итоговый тест (с взаимопроверкой)
Цель деятельности	Тестовые задания
Проверить уровень сформированности теоретических знаний учащихся за курс 7 класса и умение применять полученные знания при решении задач	(И) Учащиеся выполняют тестовые задания (см. Ресурсный материал)
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
– Оцените работы. – Составьте синквейн к изученному за 7 класс материалу		Домашнее задание: отработать задачи, вызвавшие наибольшие затруднения в решении

---

Ресурсный материал

Тест

1. Прямые т и п параллельны, k – секущая. По данным рисунка 1 найдите значение у.

2. По данным рисунка 2 найдите PK, если расстояние между прямыми МK и РТ равно 10 см.



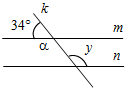
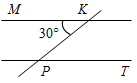
Рис. 1 Рис. 2

3. Отрезки MN и KB пересекаются в точке А. Точка А является серединой отрезка KB, и угол AKN равен углу АВМ. Найдите угол KNA, если угол ВМА равен 53°.



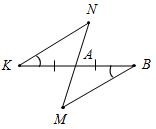
Рис. 3

4. (Задание оценивается в 4 балла.)

В равнобедренном треугольнике АВСАВ = АС. Прямая PF пересекает боковые стороны АВ и АС в точках P и F соответственно. Длина отрезка АР равна 31 дм. Угол В треугольника АВС равен углу АPF. Найдите длину отрезка АР.

5. (Задание оценивается в 5 баллов.)

Укажите номера верных утверждений.

1) Катет прямоугольного треугольника является высотой.

2) Вертикальные углы равны.

3) В треугольнике против угла в 87° лежит бо́льшая сторона.

4) Если даны две параллельные прямые, то третья прямая всегда их пересекает.

5) У любого треугольника больше одного острого угла.

6. (Задание оценивается в 6 баллов.)

В равнобедренном треугольнике MNK с основанием NM проведена медиана KD. Найдите углы треугольника KDМ и угол MKN, если внешний угол треугольника MNK при вершине N равен 130°.

Ответы: 1 – 146°; 2 – 20 см; 3 – 53°; 4 – 31 см; 5 – 1, 2, 5; 6 – 90°, 50°, 40°, 80°.

Пояснительная записка

Настоящая рабочая программа разработана в соответствии с основными положениями федерального государственного образовательного стандарта и требованиями Примерной образовательной программы основного общего образования, с учетом основных идей и положений Программы развития и формирования универсальных учебных действий и ориентирована на использование учебно-методического комплекта:

1. Геометрия. 7–9 классы : учеб. для общеобразоват. организаций / Л. С. Атанасян [и др.]. – М. : Просвещение, 2014.

2. Геометрия. 7 класс. Рабочая тетрадь : пособие для учащихся общеобразоват. организаций / Л. С. Атанасян [и др.]. – М. : Просвещение, 2014.

---

3. Геометрия. Сборник рабочих программ. 7–9 кл. / сост. Т. А. Бурмистрова. – М. : Просвещение, 2013.

4. Зив, Б. Г. Геометрия : дидактические материалы : 7 кл. / Б. Г. Зив, В. М. Мейлер. – М. : Просвещение, 2013.

5. Изучение геометрии в 7–9 классах : метод. рекомендации : кн. для учителя / Л. С. Атанасян [и др.]. – М. : Просвещение, 2011.

6. Мищенко, Т. М. Геометрия : тематические тесты : 7 кл. / Т. М. Мищенко, А. Д. Блинков. – М. : Просвещение, 2013.

Дополнительная литература для учителя:

7. Звавич, Л. И. Контрольные и проверочные работы по геометрии. 7–9 классы / Л. И. Звавич [и др.]. – М., 2001.

8. Зив, Б. Г. Задачи по геометрии : пособие для учащихся 7–11 классов общеобразоват. организаций / Б. Г. Зив, В. М. Мейлер, А. Г. Баханский. – М. : Просвещение, 2014.

9. Кукарцева, Г. И. Сборник задач по геометрии в рисунках и тестах. 7–9 классы / Г. И. Кукарцева. – М., 1999.

10. Саврасова, С. М. Упражнения по планиметрии на готовых чертежах / С. М. Саврасова, Г. А. Ястребинецкий. – М., 1987.

11. Фарков, А. В. Диагностические контрольные работы по геометрии. 7 класс / А. В. Фарков. – М., 2009.

Дополнительная литература для учащихся:

12. Шуба, М. Ю. Занимательные задания в обучении математике / М. Ю. Шуба. – М., 1997.

13. Энциклопедия для детей : в 15 т. Т. 11. Математика / под ред. М. Д. Аксенова. – М. : Аванта+, 1998.

При работе можно использовать также статьи из научно-теоретического и методического журнала «Математикав школе», из еженедельного учебно-методического приложения к газете «Первое сентября» «Математика».

Согласно действующему учебному плану рабочая программа предусматривает обучение в объеме 70 часов, 2 часа в неделю, втом числе для проведения:

– контрольных работ – 5 учебных часов;

– самостоятельных работ – 4 учебных часа;

– проектной деятельности – 5 учебных часов;

– исследовательской деятельности – 4 учебных часа.

С учетом уровневой специфики класса выстроена система учебных занятий (уроков), спроектированы цели, задачи, ожидаемые результаты обучения.

Требования к уровню подготовки учащихся 7 класса
(базовый уровень)

Должны знать:определение точки, прямой, отрезка, луча, угла; единицы измерения отрезка, угла; определение вертикальных и смежных углов, их свойства; определение перпендикулярных прямых; определение треугольника, виды треугольников, признаки равенства треугольников, свойства равнобедренного треугольника, определение медианы, биссектрисы, высоты; определение параллельных прямых, их свойства и признаки; соотношение между сторонами и углами треугольника, теорему о сумме углов треугольника; определение прямоугольного треугольника, его свойства и признаки.

---