Файл: Урок Прямая и отрезок.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 414

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Глава 1. Начальные геометрические сведения Модуль 2. Угол Цели ученика:– овладение знанием основных понятий темы: угол, вершина угла, стороны угла, градусная мера угла, острый угол, тупой угол, развернутый угол, вертикальные углы, смежные углы, свойство смежных и вертикальных углов;– совершенствование умений чертить изучаемые фигуры, обозначать их, измерять градусную меру угла, записывать результаты измерений;– совершенствование навыка проведения сравнения математических объектов (сравнение углов по величине) способом наложения и с помощью измерений, классификации объектов по признакам, выделенным в определении геометрических фигур (на примере классификации углов по их видам) Цели педагога:– создание условий для систематизации и обобщения имеющихся у учащихся представлений о геометрической фигуре «угол», его видах и измерении;– организация познавательной деятельности на уроках с целью овладения практическими навыками построения углов, способами их обозначения, измерения градусной меры углов;– разработка заданий, позволяющих организовать деятельность учащихся по овладению общими приемами сравнения геометрических фигур (на примере сравнения углов), формированию начальной геометрической культуры Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://www.uic.ssu.samara.ru/nauka/; самообразование и самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 1, вариант 2 (в рамках ЦДО) №п/п Тема и типурока Самостоятельная работа Универсальные учебные действия (УУД) Планируемые предметные результаты в предметном направлении и личностномразвитии Вид педагогической деятельности. Дидактическая модель педагогического процесса Педагогические средства Ведущая деятельность, осваиваемая в системе занятости Формы организации совзаимодействия на уроке Информационно-методическое обеспечение педагогической системы урочной и внеурочной занятости учащихся 1 2 3 4 5 6 7 8 9 10 7 Угол (применение и совершенствование знаний) [1],п. 4, 6, 9, вопросы 5–6, 10–11к гл. I,практические задания№ 41–44 Регулятивные: различать способ и результат действия.Познавательные: владеть общим приемом решения задач.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: угол, вершина угла, стороны угла, внутренняя область угла, биссектриса угла, равные фигуры (репродуктивно-алгоритмическое);– построения с помощью чертежной линейки углов, называния с помощью принятых условных обозначений сторон угла и вершины, сравнения углов наложением (продуктивно-комбинаторное);– сведений, обобщенных в презентации, о происхождении термина «биссектриса» (продуктивно-креа-тивное).Умение: проводить исследования несложных ситуаций (сравнение углов методом наложения и с помощью измерений), представить результаты своего мини-исследования, выбрать необходимое оборудование, овладевать измерительными навыками.Приобретенная компетентность: целостная, предметная, учебно-познавательная Развивающее образование.Поисковая Организация совместной учебной деятельности Познавательная, информационно-коммуникационная Групповая [8] § 2, задачи № 2 8 Сравнение и измерение углов(комбинированный) Традиционно-педагогическая. Объяснительно-иллюстративная Познавательная, информационно-коммуникационная Групповая [2].[4] § 3, задачи № 1 9 Измерение углов(применение и совершен-ствование знаний) [1],п. 9, 11, вопросы 13–14 к гл. I,практические задания№ 55–56 Регулятивные: различать способ и результат действия.Познавательные: владеть общим приемом решения задач.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: градусная мера угла, острые, тупые, прямые, развернутые, смежные, вертикальные углы (репродуктивно-алгоритмическое);– построения с помощью чертежной линейки углов, измерения их величины с помощью транспортира, записи измерения с помощью принятых условных обозначений, построения углов заданной величины, определения вида угла, применения свойств смежных и вертикальных углов (продуктивно-комбинаторное).Умение: проводить измерительные работы, классификацию по выделенному признаку (на примере определения вида углов), сравнивать объект наблюдения (угол) с эталоном (прямым углом).Приобретенная компетентность: целостная, предметная, учебно-познавательная Традиционно-педагогическая. Объяснительно-иллюстративная Специально организованное общение Учебно-познавательная Фронтальная, индивидуальная Демонстрационный транспортир. Таблица «Измерение углов».[8] § 4, задачи № 2 10 Смежные и вертикаль-ные углы (комбинированный) Компетентностно-ориентированная. Исследовательская Теоретическое исследование Учебно-познавательная Фронтальная, индивидуальная Упражнения по планимет-рии на готовых чертежах: [10], таблица № 1. [2] 11 Перпендикулярные прямые (комбинированный) [1], п. 12,вопросы 18–21к гл. I,практические задания№ 57 Регулятивные: различать способ и результат действия.Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы.Коммуникативные: контролировать действия партнера Знание:– основных понятий темы: перпендикулярные прямые, способы построения перпендикулярных прямых на местности (репродуктивно-алгоритмическое);– построения с помощью чертежного угольника перпендикулярных прямых углов, записи факта перпендикулярности прямых с помощью принятых условных обозначе-ний(продуктивно-комбинаторное).Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 1–2 алгоритмов, запи-сывать решения с помощью принятых условных обозна-чений.Приобретенная компетентность: предметная Традиционно-педагогическая. Объяснительно-иллюстративная Специально организованное общение Учебно-познавательная Фронтальная, индивидуальная Таблица «Взаимное расположение прямых на плоскости». [8] § 5.[2] 12 Контрольная работа по теме «Начальные геометрические сведения»(контроль и оценка знаний) Контрольно-оценочная. Поисковая Самостоятельное планирование и проведениерешения Рефлексивная Индивидуальная [8], контрольная работа № 1.Дифференцированныйраздаточный материал: [7], [11] Глава 2. Треугольники (18 часов) Модуль 1. Первый признак равенства треугольников Цели ученика:– овладение знанием основных понятий темы: равные треугольники, теорема-признак, соответственные элементы, первый признак равенства треугольников;– освоение умения доказывать равенство треугольников с помощью первого признака равенства треугольников;– совершенствование умения пользоваться математической символикой при записи условия и доказательства теоремы, умения проводить доказательные рассуждения Цели педагога:– создание условий для формирования у учащихся представлений о понятии «теорема», «теорема-признак»;– организация познавательной деятельности на уроках с целью овладения алгоритмом выявления равных треугольников с помощью первого признака равенства треугольников;– разработка заданий, позволяющих организовать деятельность учащихся по овладению общими приемами доказательства теорем (умением выделять в теореме условие и заключение), умением проводить доказательные рассуждения Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; http://www.rubricon.ru; http://www.encyclopedia.ru; самообразование и самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщаю-щего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 2 (в рамках ЦДО) №п/п Тема и типурока Самостоятельная работа Универсальные учебные действия (УУД) Планируемые предметные результаты в предметном направлении и личностномразвитии Вид педагогической деятельности. Дидактическая модель педагогического процесса Педагогические средства Ведущая деятельность, осваиваемая в системе занятости Формы организации совзаимодействия на уроке Информационно-методическое обеспечение педагогической системы урочной и внеурочной занятости учащихся 1 2 3 4 5 6 7 8 9 10 13 Треугольники (изучение нового материала) [1],п. 14, 15, вопросы 1–4 к гл. II,практические задания№ 87–89 Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы Знание:– основных понятий темы: треугольник, вершина, сторона, угол треугольника, периметр треугольника, равные треугольники, соответственные элементы, первый признак равенства треугольников (репродуктивно-алгоритмическое);– построения треугольников, проведения измерений его элементов, записи результатов измерений, нахождения периметра;– перевода текста (формулировки) первого признака равенства треугольников в графический образ, короткой записи, проведения доказательства, применения для решения задач на выявление равных треугольников (продуктивно-комбинаторное);– презентация «Треугольники вокруг нас» (продуктивно-креативное).Умение:– переводить текстовую информацию в графический образ и математическую модель, представлять информацию в сжатом виде – схематичной записи формулировки теоремы;– проводить доказательные рассуждения, понимать специфику математического языка.Приобретенная компетентность: предметная Развивающее образование.Поисковая Беседа, демонстрация Учебно-познавательная Фронтальная, индивидуальная Таблицы «Равные треугольники», «Признаки равенства треугольников» 14 Первый признакравенства треугольников (комбинированный) Развивающее образование. Поисковая Проблемные задачи Учебно-познавательная Фронтальная, индивидуальная [2].[8] § 7, вари-анты 1–3.Модели треугольников 15 Первый признакравенства треугольников (применение и совершенствование знаний) [1],п. 15–17, вопросы 7–9 к гл. II,практические задания№ 100–103 Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.Познавательные: строить речевое высказывание в устной и письменной форме.Коммуникативные: контролировать действия партнера Традиционно-педагогическая. Поисковая Практикум Познавательная, информационно-коммуникационная Групповая Упражнения по планимет-рии на готовых чертежах: [4], таблица № 2.[8] § 7, вари-анты 4–8 16 Медиана, биссектриса и высота треугольника (изучение нового материала) Знание:– основных понятий темы: медиана, высота, биссектриса (репродуктивно-алгоритмическое);– построения с помощью чертежного угольника и транспортира медианы, высоты, биссектрисы прямоугольного треугольника (продуктивно-комбинаторное);– сведений, обобщенных в презентации, о возникновении и значении термина «медиана» и «биссектриса»(продуктивно-креативное).Умение:грамотно выполнять алгоритмические предписания и инструкции (на примере построения медиан, высот, биссектрис треугольника), овладевать азами графической культуры.Приобретенная компетентность: предметная, учебно-познавательная Развивающее образование.Поисковая Лабораторно-графическая работа Учебно-познавательная Фронтальная, индивидуальная [8] § 8, задачи № 1.[2] 17 Свойства равнобедренного треугольника (комбинированный) [1],п. 18, вопросы 10–13 кгл. II,практические задания№ 104 Регулятивные:различать способ и результат действия.Познавательные: владеть общим приемом решения задач; ориентироваться на разнообразие способов решения задач.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов; контролировать действия партнера Знание:– основных понятий темы: равнобедренный треугольник, основание, боковые стороны, равносторонний треугольник (репродуктивно-алгоритмическое);– доказательства и применения при решении теоремы о свойствах равнобедренного треугольника (продуктивно-комбинаторное).Умение: проводить исследования несложных ситуаций (сравнение элементов равнобедренного треугольника), формулировать гипотезы исследования, понимать необходимость ее проверки, доказательства, совместно работать в группе.Приобретенная компетентность: целостная, предметная, учебно-познавательная Компетентностно-ориентированная. Исследовательская Организация совместной учебной деятельности Познавательная, информационно-коммуникационная Групповая Упражненияпо планимет-рии на готовых чертежах: [10], таблица № 3.[8] § 8, задачи № 2 18 Свойства равнобедренного треугольника (комбинированный) Компетентностно-ориентированная. Исследовательская Познавательная, информационно-коммуникационная Групповая Упражненияпо планимет-рии на готовых чертежах: [10], таблица № 4 1   ...   39   40   41   42   43   44   45   46   47

Глава 3. Параллельные прямые (12 часов) Модуль 1. Признаки параллельности прямых Цели ученика:– овладение умением читать, записывать (в схематичном виде) признаки параллельности двух прямых;– освоение способов выявления параллельных прямых среди данных, умения доказывать свои предположения по поводу параллельности прямых с помощью изученных теорем-признаков;– совершенствование умения использовать математическую символику при записи решения задач на доказательство параллельности прямых Цели педагога:– создание условий для формирования у учащихся представлений о параллельности прямых;– организация познавательной деятельности по развитию умений различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач по выявлению признаков параллельности двух прямых и способов их доказательства;– разработка практических заданий, позволяющих формировать у учащихся понимание специфики математического языка и навыки работы с математической символикой Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://www.uic.ssu.samara.ru/nauka; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 15 (в рамках ЦДО) №п/п Тема и типурока Самостоятельная работа Универсальные учебные действия (УУД) Планируемые предметные результаты в предметном направлении и личностномразвитии Вид педагогической деятельности. Дидактическая модель педагогического процесса Педагогические средства Ведущая деятельность, осваиваемая в системе занятости Формы организации совзаимодействия на уроке Информационно-методическое обеспечение педагогической системы урочной и внеурочной занятости учащихся 1 2 3 4 5 6 7 8 9 10 31 Параллельные прямые(комбинированный) [1],п. 24–25, вопросы 1–3к гл. III Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок.Познавательные: владеть общим приемом решения задач.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: параллельные прямые, секущая, названия углов, образованных при пересечении двух прямых секущей (репродуктивно-алгоритмическое);– накрест лежащих, односторонних, соответственных углов, перевода текста (формулировки) признаков параллельности в графический образ (продуктивно-комбинаторное).Умение:– передавать содержание прослушанного материала в сжатом виде (конспект);– структурировать материал, понимать специфику математического языка и работы с математической символикой.Приобретенная компетентность: предметная, целостная Традиционно-педагогическая. Объяснительно-иллюстративная Лекция, демонстрация Учебно-познавательная Учебно-познавательная Таблица «Признаки параллель-ности прямых на плоскости» 32 Признаки параллельности двух прямых(изучение нового материала) Развивающее образование.Поисковая Проблемное изложение Учебно-познавательная Фронтальная, индивидуальная Упражнения по планимет-рии на готовых чертежах: [10], таблица № 5 33 Признаки параллельности двух прямых(комбинированный) [1],п. 25, вопросы 4–6 к гл. III Регулятивные: различать способ и результат действия.Познавательные: владеть общим приемом решения задач.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: параллельные прямые, секущая, названия углов, образованных при пересечении двух прямых секущей (репродуктивно-алгоритмическое);– накрест лежащих, односторонних, соответственных углов, параллельности прямых на основе признаков параллельности, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение: – работать с готовыми предметными, знаковыми и графическими моделями для описания свойств и качеств изучаемых объектов;– проводить классификацию объектов (параллельные, непараллельные прямые) по заданным признакам.Приобретенная компетентность: предметная, целостная Развивающее образование.Поисковая Организация совместной учебной деятельности Познавательная, информационно-коммуникационная Групповая [8] § 13.[2] 34 Признаки параллельности двух прямых(применение и совершенствование знаний) Развивающее образование.Поисковая Познавательная, информационно-коммуникационная Групповая [9] 35 Практические способы постро-ения параллельных прямых (комбинированный) [1],п. 25–26, вопросы 1–6к гл. III Регулятивные:учитывать правило в планировании и контроле способа ре-шения.Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы.Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве Знание:– общего способа действий по построению параллельных прямых (репродуктивно-алгоритмическое);– построения параллельных прямых по выработанному алгоритму, записи выполняемых действий с помощью принятых обозначений, доказательства параллельности построенных прямых (продуктивно-комбинаторное).Умение:использовать соответствующие инструменты для решения практических задач, точно выполнять инструкции.Приобретенная компетентность: предметная Развивающее образование. Поисковая Беседа, демонстрация, графическая работа Познавательная, информационно-коммуникационная Фронтальная,парная(взаимопроверка) Демонстрационный чертежный треугольник, раздаточный материал для графической работы, цветные ручки для взаимопроверки 36 Зачетпо теме «Признаки параллельности двух прямых»(контроль и оценка знаний) Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок.Познавательные: строить речевое высказывание в устной и письменной форме.Коммуникативные: контролировать действия партнера Знание:– признаков параллельности прямых и их доказательства(репродуктивно-алгоритмическое);– построения параллельных прямых, способов решения задач по теме (продуктивно-комбинаторное).Умение: распределить свою работу, оценить уровень владения материалом.Приобретенная компетентность: целостная Контрольно-оценочная. Поисковая Выполнение зачетных заданий Рефлексивная Индивидуальная Карточки с вопросами к зачету Глава 3. Параллельные прямые Модуль 2. Аксиома параллельных прямых Цели ученика:– овладение умением определять содержание ключевого понятия «теорема, обратная к данной»;– освоение умения находить неизвестные углы, образованные двумя параллельными прямыми и секущей;– осваивание умений различать факт, гипотезу, развивать способность проводить доказательные рассуждения Цели педагога:– организация познавательной деятельности по решению поисковых задач на основе изученных теорем;– создание условий для формирования у учащихся представлений о понятии «теорема, обратная к данной» на примере теорем об углах, образованных двумя параллельными прямыми и секущей;– разработка заданий, позволяющих организовать деятельность учащихся по развитию умения различать факт, гипотезу, проводить доказательство в ходе изучения теорем по данной теме Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тесты № 16, 17 (в рамках ЦДО) №п/п Тема и типурока Самостоятельная работа Универсальные учебные действия (УУД) Планируемые предметные результаты в предметном направлении и личностномразвитии Вид педагогической деятельности. Дидактическая модель педагогического процесса Педагогические средства Ведущая деятельность, осваиваемая в системе занятости Формы организации совзаимодействия на уроке Информационно-методическое обеспечение педагогической системы урочной и внеурочной занятости учащихся 1 2 3 4 5 6 7 8 9 10 37 Аксиома параллельных прямых(комбинированный) [1],п. 27–28, вопросы 7–10 к гл. III Регулятивные: различать способ и результат действия.Познавательные: владеть общим приемом решения задач.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– содержания ключевых понятий: аксиома, аксиоматический подход в геометрии, теорема, обратная к данной, теорема-следствие (репродуктивно-алгоритмическое);– формулировки аксиомы параллельных прямых, следствий из аксиомы параллельных прямых, определения параллельности прямых на основе нового признака параллельности, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение: работать с готовыми графическими моделями для описания свойств и качеств изучаемых объектов, проводить классификацию объектов (углов, полученных при пересечении двух прямых) по заданным признакам.Приобретенная компетентность: предметная, целостная Традиционно-педагогическая. Объяснительно-иллюстративная Работа с текстом учебника Учебно-познавательная Фронтальная, индивидуальная Портреты ученых (Евклид, Лобачевский) 38 Теоремыоб углах, образованных двумя параллельными прямыми и секущей(комбинированный) Традиционно-педагогическая. Объяснительно-иллюстративная Практикум Учебно-познавательная Фронтальная, индивидуальная [2].[8] § 14.Таблица «Углы, образованные двумя параллельными прямыми и секущей» 39 Теоремыоб углах, образованных двумя параллельными прямыми и секущей (комбинированный) [1],п. 29, вопросы 11–15 к гл. III Регулятивные: вносить необходимые коррективы в действие после его завершения на основе его и учета характера сделанных ошибок.Познавательные: строить речевое высказывание в устной и письменной форме.Коммуникативные: контролировать действия партнера Знание:– основных понятий темы: параллельные прямые, секущая, названий углов, образованных при пересечении двух параллельных прямых секущей (накрест лежащие, односторонние, соответственные) (репродуктивно-алгоритмическое);– способов решения задач на вычисление углов, образованных двумя параллельными прямыми и секущей, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение: переводить текстовую информацию в графический образ и математическую модель, представлять информацию в сжатом виде – схематичная запись формулировки теоремы, проводить доказательные рассуждения, понимать специфику математического языка.Приобретенная компетентность: предметная Компетентностно-ориентированная. Исследовательская Организация совместной учебной деятельности Познавательная, информационно-коммуникационная Групповая Упражнения по планимет-рии на готовых чертежах: [10], таблица № 7 40 Теоремыоб углах, образованных двумя параллельными прямыми и секущей(комбинированный) Компетентностно-ориентированная. Исследовательская Организация совместной учебной деятельности Познавательная, информационно-коммуникационная Групповая [8] § 15, 16 41 Теоремыоб углах, образованных двумяпараллельными пря-мыми(обобщающий) [1],п. 24–29.Повторение всей главы Регулятивные:учитывать правило в планировании и контроле способа решения.Познавательные: строить речевое высказывание в устной и письменнойформе.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: параллельные прямые, секущая, названий углов, образованных при пересечении двух параллельных прямых секущей (накрест лежащие, односторонние, соответственные) (репродуктивно-алгоритмическое);– способов решения задач на вычисление углов, образованных двумя параллельными прямыми и секущей, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение: объяснять изученные положения на самостоятельно подобранных примерах, проводить классификацию (на примере видов углов при двух параллельных и секущей) по выделенным признакам, доказательныерассуждения.Приобретенная компетентность: предметная, целостная Фронтальная. Индивидуальная Специально организованное общение Учебно-познавательная Фронтальная, индивидуальная [2] 42 Контрольная работа по теме «Параллельность прямых» (контроль и оценка знаний) Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок.Познавательные: строить речевое высказывание в устной и письменной форме.Коммуникативные: контролировать действия партнера Контрольно-оценочная. Поисковая Разноуровневые задания Рефлексивная Индивидуальная [8], контрольная работа № 3.Дифференцированный раздаточный материал:[7], [11] 1   ...   39   40   41   42   43   44   45   46   47

Глава 4. Соотношения между сторонами и углами треугольника (18 часов) Модуль 1. Соотношение между сторонами и углами треугольника Цели ученика:– формирование представлений о соотношении между сторонами и углами треугольника;– овладение умением различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач на выявление соотношений сторон и углов в треугольнике Цели учителя:– создание условий для формирования у учащихся представлений о соотношении между сторонами и углами треугольника;– организация познавательной деятельности по развитию умения различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач на выявление соотношений сторон и углов в треугольнике;– усвоения навыков доказательства соотношений сторон и углов в треугольнике;– формирования умений применять полученные знания в учебной деятельности Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://mega.km.ru; http://www.rubricon.ru; http://www. encyclopedia.ru; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тест № 18 (в рамках ЦДО) №п/п Тема и типурока Самостоятельная работа Универсальные учебные действия (УУД) Планируемые предметные результаты в предметном направлении и личностномразвитии Вид педагогической деятельности. Дидактическая модель педагогического процесса Педагогические средства Ведущая деятельность, осваиваемая в системе занятости Формы организации совзаимодействия на уроке Информационно-методическое обеспечение педагогической системы урочной и внеурочной занятости учащихся 1 2 3 4 5 6 7 8 9 10 43 Сумма углов треугольника(изучение нового материала) [1],п. 30–31, вопросы 1–5к гл. IV Регулятивные:учитывать правило в планировании и контроле способа решения.Познавательные: ориентироваться на разнообразие способов решения задач.Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве Знание:– содержания ключевых понятий: внутренний угол треугольника, внешний угол треугольника, сумма углов треугольника (репродуктивно-алгоритмическое);– теорем о сумме углов треугольника и свойстве внешнего угла треугольника, способов их доказательства, алгоритмов решения задач на нахождение углов треугольника, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение: проводить исследования несложных ситуаций (измерение углов треугольника и вычисление их суммы), формулировать гипотезу исследования, понимать необходимость ее проверки, совместно работать в группе.Приобретенная компетентность: целостная, учебно-познавательная Компетентностно-ориентированная. Исследовательская Теоретическое исследование Познавательная, информационно-коммуникационная Групповая [8] § 17.Наборы треугольников, транспортир, рабочие листы с заданием для работы группы 44 Сумма углов треугольника(изучение нового материала) Компетентностно-ориентированная. Исследовательская Теоретическое исследование Познавательная, информационно-коммуникационная Групповая Упражнения по планимет-рии на готовых чертежах: [10], таблица № 8, 9 45 Соотношение между сторонами и углами треугольника (комбинированный) [1],п. 32, вопросы6–11к гл. IV Регулятивные: различать способ и результат действия.Познавательные: проводить сравнение, сериацию и классификацию по заданным критериям.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– содержания ключевых понятий: угол, противолежащий стороне, неравенство треугольников (репродуктивно-алгоритмическое);– теорем о соотношении между сторонами и углами треугольника, их доказательства и способов применения в решении задач, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение:– составлять конспект математического текста, выделять главное, формулировать определения по описанию математических объектов;– осуществлять перевод понятий из печатного (текст) в графический образ (чертеж).Приобретенная компетентность: учебно-познавательная, информационная Традиционно-педагогическая. Объяснительно-иллюстративная Работа с текстом учебника Учебно-познавательная Фронтальная, индивидуальная [2].[8] § 18, 19 46 Соотношение между сторонами и углами треугольника (комбинированный) Традиционно-педагогическая. Объяснительно-иллюстративная Практикум Учебно-познавательная Фронтальная, индивидуальная [9] 47 Соотношение между сторонами и углами треугольника (обобщающий) [1],п. 33–34, вопросы 12–17к гл. IV Регулятивные: оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.Познавательные: строить речевое высказывание в устной и письменной форме.Коммуникативные: контролировать действия партнера Знание:– содержания ключевых понятий: внутренний угол треугольника, внешний угол треугольника, сумма углов треугольника, неравенство треугольников (репродуктивно-алгоритмическое);– теорем о сумме углов треугольника и свойстве внешнего угла треугольника, способов их доказательства, алгоритмов решения задач на нахождение углов треугольника, записи решения с помощью принятых обозначений (продуктивно-комбинаторное).Умение:приводить примеры, подбирать аргументы, вступать в речевое общение, участвовать в коллективной деятельности, оценивать работы других.Приобретенная компетентность: целостная, учебно-познавательная Развивающее образование.Поисковая Организация совместной учебной деятельности Познавательная, информационно-коммуникационная Групповая [2] 48 Контрольная работа по теме «Сумма углов треугольника» (контроль и оценка знаний) Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве Контрольно-оценочная. Поисковая Разноуровневые задания Рефлексивная Индивидуальная Дифференцированныйраздаточныйматериал:[7], [11] Глава 4. Соотношения между сторонами и углами треугольника Модуль 2. Прямоугольные треугольники Цели ученика:– формирование представлений о признаках равенства прямоугольных треугольников;– овладение общими приемами решения поисковых задач;– совершенствование умения использовать для познания окружающего мира различные методы (наблюдение, измерение, моделирование), работать с полученной моделью Цели педагога:– создание условий для формирования у учащихся представлений о признаках равенства прямоугольных треугольников;– организация познавательной деятельности по решению поисковых задач на основе изученных теорем;– разработка заданий, позволяющих совершенствовать умение использовать для познания окружающего мира различные методы (наблюдение, измерение, моделирование) и умение работать с полученной моделью Внеурочная деятельность: поиск информации с использованием интернет-ресурсов: http://www.uic.ssu.samara.ru/nauka; самоконтроль знаний по сборнику: Геометрия. 7–9 классы: тесты для текущего и обобщающего контроля / авт.-сост. Г. И. Ковалева, Н. И. Мазурова. Волгоград: Учитель, 2007. Тесты № 19, 20, 22 (в рамках ЦДО) №п/п Тема и типурока Самостоятельная работа Универсальные учебные действия (УУД) Планируемые предметные результаты в предметном направлении и личностномразвитии Вид педагогической деятельности. Дидактическая модель педагогического процесса Педагогические средства Ведущая деятельность, осваиваемая в системе занятости Формы организации совзаимодействия на уроке Информационно-методическое обеспечение педагогической системы урочной и внеурочной занятости учащихся 1 2 3 4 5 6 7 8 9 10 49 Прямоугольные треугольники (комбинированный) [1],п. 35, вопросы9–11к гл. IV Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок.Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы.Коммуникативные: контролировать действия партнера Знание:– основных понятий темы: прямоугольный треугольник, катет, гипотенуза, свойство острых углов треугольника, свойство прямоугольного треугольника с углом в 30° (репродуктивно-алгоритмическое);– доказательств свойств прямоугольного треугольника, применения их при решении поисковых задач (продуктивно-комбинаторное).Умение: различать факт, гипотезу, проводить доказательные рассуждения в ходе решения исследовательских задач на выявление соотношений углов прямоугольного треугольника.Приобретенная компетентность: предметная, целостная Традиционно-педагогическая. Объяснительно-иллюстративная Специально организованное общение Учебно-познавательная Фронтальная, индивидуальная Таблица «Свойства прямоуголь-ного треугольника» 50 Прямоугольные треугольники (комбинированный) Развивающее образование.Поисковая Проблемные задания Учебно-познавательная Фронтальная, индивидуальная [2].[8] § 13 51 Прямоугольные треугольники (применение и совершенствование знаний) [1],п. 35, 36, вопросы 12–13к гл. IV Регулятивные: различать способ и результат действия.Познавательные: проводить сравнение, классификацию по заданным критериям.Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: прямоугольный треугольник, катет, гипотенуза, признаки равенства прямоугольных треугольников (репродуктивно-алгоритмическое);– доказательств признаков равенства прямоугольных треугольников, способов решения задач на доказательство равенства прямоугольных треугольников, записи доказательства с помощью специальной символики (продуктивно-комбинаторное).Умение: проводить исследования несложных ситуаций (сравнение прямоугольных треугольников), представлять результаты своего мини-исследования, выбирать соответствующий признак для сравнения, работать в группе.Приобретенная компетентность: целостная, предметная, учебно-познавательная Развивающее образование.Поисковая Теоретическое исследование Познавательная, информационно-коммуникационная Групповая Таблица «Признаки равенства прямоугольных треугольников» 52 Прямоугольные треугольники (применение и совершенствование знаний) Развивающее образование.Поисковая Проблемные задания Познавательная, информационно-коммуникационная Групповая [9] 53 Решение задач (применение и совершен-ствование знаний) [1],п. 34–36, вопросы 12–13к гл. IV Регулятивные: вносить необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.Познавательные: владеть общим приемом решения задач.Коммуникативные: договариваться и приходить к общему решению в со-вместной деятельности, в том числе в ситуации столкновения интересов Знание:– основных понятий темы: прямоугольный треугольник, катет, гипотенуза, признаки равенства прямоугольных треугольников (репродуктивно-алгоритмическое);– доказательств признаков равенства прямоугольных треугольников, способов решения задач на доказательство равенства прямоугольных треугольников, записи доказательства с помощью специальной символики (продуктивно-комбинаторное).Умение: переводить текстовую информацию в графический образ и математическую модель, решать комбинированные задачи с использованием 2–3 алгоритмов, проводить доказательные рассуждения в ходе презентации решения задач, составлять обобщающие таблицы.Приобретенная компетентность: предметная Компетентностно-ориентированная. Исследовательская Организация совместной учебной деятельности Учебно-познавательная Групповая (группы сменного состава) Дифференцированный раздаточный материал 54 Решение задач (применение и совершен-ствование знаний) Компетентностно-ориентированная. Исследовательская Организация совместной учебной деятельности Учебно-познавательная Групповая (группы сменного состава) Дифференцированный раздаточный материал 1   ...   39   40   41   42   43   44   45   46   47



Ресурсный материал

Самостоятельная работа

Вариант I

1. Дано:AOB = 122°, AOD = 19°, COB = 23° (рис. 1).

Найти:COD.

а) 90°; б) 80°; в) 164°.

2. Дано: луч ОС проходит между сторонами угла АОВ, равного 120°.

Найти:AOC, если AOC меньше СОВ в 2 раза.



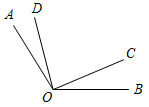
Рис. 1

а) 80°; б) 60°; в) 40°.

3. Может ли луч с проходить между сторонами угла ab, если ab = 130°, ac = 40°, cb = 90°?

а) Да; б) нет; в) в условии не хватает данных.

Вариант II

1. Дано:AOD = 22°, DOC = 47°, AOB = 132° (рис. 2).

Найти:СОВ.

а) 63°; б) 53°; в) 157°.

2. Дано: луч ОС проходит между сторонами угла АОВ, равного 120°.

Найти:СОВ, если AOC на 30° больше СОВ.



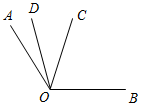
Рис. 2

а) 75°; б) 90°; в) 45°.

3. Может ли луч с проходить между сторонами ab, если ab = 50°, ac= 120°, cb = 70°?

а) Да; б) нет; в) в условии не хватает данных.

Ответы:

№
Вариант I
Вариант II

1
б
а

2
в
в

3
а
б
1   2   3   4   5   6   7   8   9   ...   47


Урок8. Перпендикулярные прямые

Цели деятельности
учителя
Создать условия для повторения понятия перпендикулярных прямых, рассмотрения свойства перпендикулярных прямых; совершенствовать у учащихся умение решать задачи

Термины и понятия
Угол, смежные углы, вертикальные углы, перпендикулярные прямые

Планируемые результаты

Предметные умения
Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: умеют слушать партнера, формулировать, аргументировать и отстаивать свое мнение.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы
Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные
ресурсы

• Чертежи к задачам.

• Задания для парной работы




I этап. Актуализация опорных знаний учащихся

Цель деятельности
Совместная деятельность

Систематизировать
теоретические знания
(Ф/И)

1. Обсуждение вопросов учащихся по домашнему заданию.

2. Выполнение задания: на каком рисунке изображены смежные углы?



а) б)



в) г)

II этап. Решение задач по готовым чертежам

Цель деятельности
Совместная деятельность

Совершенствовать
навыки решения задач
(П) Выполнение заданий и взаимопроверка.

1. Дано: – β = 30°. 3. Дано: ОЕ – биссектриса COD; DOE = 32°.

Найти:, β. Найти:BOC, AOF.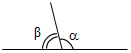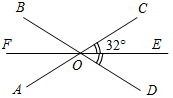



Рис. 1 Рис. 3

Ответ:  = 105°, β = 75°. Ответ: BOC = 180° – COD = 116°; AOF = COE = 32°.

2. Дано:ABD : CBD = 1 : 5.4. Дано:АОВ = (ВОС + COD + DОА).

Найти:AOB, BOC.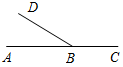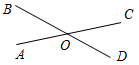



Рис. 2 Рис. 4

Ответ: ABD = 30°, CBD = 150°. Ответ: AOB = (360° – AOB), AOB = 40°, BOC = 140°

III этап. Изучение нового материала

Цель деятельности
Совместная деятельность

Ввести понятие перпендикулярных прямых
(Ф/И)

При изучении нового материала можно опираться на имеющиеся у учащихся знания по данной теме за курс математики 6 класса.

– Какие прямые называются перпендикулярными? (Две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.)

– Запишите, используя математические символы: «Прямая АВ перпендикулярна прямой CD». Выполните соответствующий рисунок и укажите все углы.

– Пересекаются ли две прямые, перпендикулярные третьей? (Нет.)

Учащиеся могут вспомнить, что такие прямые параллельны.

– Две прямые, перпендикулярные третьей, не пересекаются – это свойство перпендикулярных прямых. Докажем это свойство (п. 12 учебника). (Доказывает учитель.)

П. 13 «Построение прямых углов на местности» можно порекомендовать прочитать дома

IV этап. Решение задач

Цель деятельности
Совместная деятельность

Совершенствовать
навыки решения задач по изученной теме
(П) После выполнения заданий представить решение задач на доске.

№ 1.

Два тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны.

Найдите величину тупых углов, если известно, что они равны.

Решение:

AOB = AOC. ВООС, значит, ВОС = 90°.

Так как AOB = AOC, то 2АОВ = 360° – 90° = 270°, АОВ = 135°.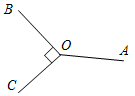



Рис. 5

№ 2.

Из вершины развернутого угла проведены два луча, которые делят его на три равные части.

Докажем, что биссектриса среднего угла перпендикулярна сторонам развернутого угла.

Решение:

AOB = ВОС = COD = 60°. OK – биссектриса ВОС, тогда COK = ВОK = 30°, следовательно,
DОK = 60° + 30° = 90°, AOK = 60° + 30° = 90°, то есть OKОА, OKOD.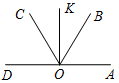



Рис. 6

№ 3.

Углы АОВ и DОС смежные, OМ – биссектриса AOB, луч ON принадлежит внутренней области ВОС и перпендикулярен ОМ. Является ли ON биссектрисой BOC? Почему?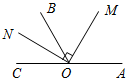



Рис. 7

Решение:

AOB и ВОС смежные, значит, AOB = 180° – BOC, а так как ОМ – биссектриса АОВ, то ВОМ =
= МОА = (180° – ВОС) = 90° – ВОС. Так как ONОМ, то MON = 90°, a ВОМ = 90° – BON.
Получили, что ВОМ = 90° – ВОС = 90° – BON, откуда следует, что ВОС = ВОN, то есть ОNявляется биссектрисой ВОС

V этап. Итоги урока. Рефлексия

Деятельность учителя
Деятельность учащихся

(Ф/И)

– Оцените свою работу на уроке и работу своих
товарищей.

– Что нового узнали на уроке?
(И) Домашнее задание: решить задачи № 66, 68 и дополнительные задачи.

1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.

2. Сумма трех углов, образовавшихся при пересечении двух прямых, равна 325°.
Найдите остальные углы


Урок9. Решение задач

Цели деятельности учителя
Создать условия для повторения, закрепления материала главы I; совершенствовать навыки решения задач; подготовить учащихся к предстоящей контрольной работе

Термины и понятия
Угол, смежные углы, вертикальные углы, перпендикулярные прямые, биссектриса угла, луч, отрезок

Планируемые результаты

Предметные умения
Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям.

Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок: осуществляют самоанализ и самоконтроль.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: осознают важность и необходимость изучения предмета

Организация пространства

Формы работы
Фронтальная (Ф); индивидуальная (И)

Образовательные
ресурсы

• Задания для самостоятельной работы.

• Тест
1   2   3   4   5   6   7   8   9   ...   47




I этап. Актуализация знаний учащихся

Цель деятельности

Совместная деятельность

Проверить уровень сформированности теоретических знаний
(Ф/И)

Проверка домашнего задания. К доске вызываются двое учащихся.

№ 66.

а) Если 2 + 4 = 220°, так как 2, 4 – вертикальные, то 2 = 4 = 220° : 2 = 110°.

1 = 3 = 70° (смежные с 2 и 4).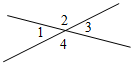



Рис. 1

Ответ: 70°, 110°, 70°, 110°.

б) Если 3 · (1 + 3) = 2 + 4, в) Если 2 – 1 = 30°. Примем 1 = х, следовательно:

так как 1 = 3 = х, 2 = х + 30°

то 2 = 4 = 180° – х подставим в условие: х + х + 30° = 180°

3 · (х + х) = 180° – х + 180° – х 2х = 150°

6х = 360° – 2х х = 75°

8х = 360° 1 = 75°, 2 = 105°

х = 45° Ответ: 75°, 105°.

1 = 3 = 45°, 2 = 4 = 135°

Ответ: 45°, 135°, 45°, 135°.

№ 68.

Дано: ADBEFC = O, AOB = 50°, FOE = 70°.

Найти:АОС, BOD, COE, COD.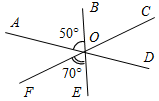



Рис. 2

Решение:

1) EOD = AOB = 50°.

2) FOD = FOE + EOD = 70° + 50° = 120°.

3) COD = 180° – FOD = 180° – 120° = 60°.

4) AOB = 50° + 70° = 120°; COE = 60° + 50° = 110°; BOD = 70° + 60° = 130°, COD = 60°.

Ответ: 120°, 130°, 110°, 60°

II этап. Самостоятельная работа

Цель деятельности
Задания для самостоятельной работы

Проверить уровень сформированности знаний при решении простейших задач
(И) Работа рассчитана на 10–15 минут. Далее осуществляется взаимопроверка.

Вариант I

1. Смежные углы относятся как 1 : 2. Найдите эти смежные углы.

2. Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.

3. Дано: = 30°, β = 140°.

Найти:1, 2, 3, 4.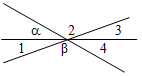



Рис. 3

Вариант II

1. Один из смежных углов больше другого на 20°. Найдите эти смежные углы.

2. Один из углов, образовавшихся при пересечении двух прямых, равен 102°. Найдите остальные углы.

3. Дано: = 20°, β = 130°.

Найти:1, 2, 3, 4.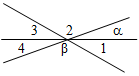


Рис. 4

Решение:

Вариант I

1. Так как 1 : 2 = 1 : 2, то 1 = х, 2 = 2х. Но 1 + 2 = 180°,тогда х + 2х = 180°, х = 60, значит, 1 = 60°, 2 = 120°.



Рис. 5

2. Пусть 1 = 21°, тогда 3 = 1, как вертикальные, и 3 = 21°. 1 и 2 – смежные и 1 + 2 = 180°.

Тогда 2 = 180° – l = 159°. Но 2 = 4, как вертикальные, значит, 4 = 159°.



Рис. 6

3.  = 30°, тогда 4 = 30°, так как 4 и угол с градусной мерой  – вертикальные. β = 140°, тогда 2 = 140°, так как 2 и угол с градусной мерой β – вертикальные.

2 + 3 + 4 = 180°, тогда 3 = 180° – (2 + 4) = 10°.

3 и 1 – вертикальные, поэтому 3 = 1, 1 = 10°.

Вариант II

1. 2 на 20° больше 1, тогда 1 = х, 2 = х + 20°. Но 1 + 2 = 180°, тогда х + х + 20° = 180°, х = 80°, значит, 1 = 80°, 2 = 100°.



Рис. 7

2. Пусть 1 = 102°, тогда 3 = 1, как вертикальные, и 3 = 102°. 1 и 2 – смежные и 1 + 2 = 180°, тогда 2 = 180° – 1 = 78°. Но 2 = 4, как вертикальные, значит, 4 = 78°.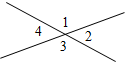



Рис. 8

3.  = 20°, тогда 4 = 20°, так как 4 и угол с градусной мерой  – вертикальные. β = 130°, тогда 2 = 130°, так как 2 и угол с градусной мерой β – вертикальные.

2 + 3 + 4 = 180°, тогда 3 = 180° – (2 + 4) = 30°.

3 и 1 – вертикальные, поэтому 3 = 1, 1 = 30°

III этап. Тест

Цель деятельности
Тестовые задания

Повторить теоретический материал
(И)

1. Точка С лежит на луче АВ. Какая из точек А, В, С лежит между двумя другими?

а) А; в) С;

б) В или С; г) В.

2. Отрезок ХМ пересекает прямую а. Отрезок XD пересекает прямую а. Пересекает ли прямую а отрезок МD?

а) Да; в) никогда не пересекает;

б) может не пересекать; г) нет правильного ответа.

3. Один из углов, образованных при пересечении двух прямых, – прямой. Остальные углы…

а) острые и прямой; в) прямые;

б) тупые и прямой; г) нет правильного ответа.

4. Сумма двух углов, образованных при пересечении двух прямых, равна 180°. Эти углы…

а) смежные; в) нет правильного ответа;

б) вертикальные; г) могут быть смежными, могут быть вертикальными.

5. Если точка В принадлежит отрезку АС, то...

а) АВ + ВС = АС; в) ВС + АС = АВ;

б) АВ + АС = ВС; г) нет правильного ответа.

6. Если луч ОС проходит между сторонами угла АОВ, то...

a) AOC = BOC; в) AOB + BOC = AOC;

б) AOC + BOC = AOB; г) AOC + AOB = BOC.

7. Если точка В – середина отрезка АС, то…

а) АВ + ВС = АС; в) АВ = 2АС;

б) АС = ВС; г) АС = 2АВ.

8. Если луч ОС – биссектриса AOB, то…

a) AOB = AOC + BOC; в) AOC = BOC;

б) AOC = AOB; г) AOB ≠ BOC.

Ответы: 1 – б; 2 – г; 3 – в; 4 – г; 5 – а; 6 – б; 7 – г; 8 – в

IV этап. Итоги урока. Рефлексия

Деятельность учителя
Деятельность учащихся

(Ф/И)

– Оцените свою работу на уроке.

– Какие понятия повторяли на уроке?
(И) Домашнее задание: решить задачи № 74, 75, 80, 82


Урок10. Контрольная работа № 1

Цель деятельности учителя
Создать условия для проверки знаний, умений навыков учащихся по теме «Измерение отрезков. Измерение углов. Смежные и вертикальные углы»

Термины и понятия
Угол, смежные углы, вертикальные углы, перпендикулярные прямые, биссектриса угла, луч, отрезок

Планируемые результаты

Предметные умения
Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям.

Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и контроль своей учебной деятельности.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: осознают необходимость и важность изучения предмета

Организация пространства

Формы работы
Фронтальная (Ф); индивидуальная (И)

Образовательные
ресурсы

• Задания для контрольной работы




I этап. Выполнение контрольной работы по вариантам

Цель деятельности

Задания для контрольной работы

Проверить уровень знаний и умений по изученной теме
(И)

Вариант I

1. Три точки В, С и D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?

2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.

3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.

Вариант II

1. Три точки М, N и K лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МK?

2. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.

3. С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов.

Вариант III (для более подготовленных учащихся)

1. Лежат ли точки M, N и P на одной прямой, если MP = 12 см, MN = 5 см, PN = 8 см?

2. Найдите неразвернутые углы, образованные при пересечении двух прямых, если разность двух из них равна 37°.

3. На рисунке АВСD, луч ОЕ – биссектриса угла АОD. Найдите угол СОЕ.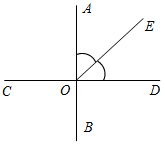



II этап. Итоги урока. Рефлексия

Деятельность учителя
Деятельность учащихся

(Ф/И)

– Что выполняли на уроке?

– Какие задания вызвали затруднения? Почему?

– Как оцениваете свою работу на уроке?
(И)

Домашнее задание: повторить § 1–6
1   2   3   4   5   6   7   8   9   ...   47

Смотрите также файлы