Файл: Урок Прямая и отрезок.docx

Урок11. Треугольник

Цели деятельности учителя		Создать условия для введения понятий треугольника и его элементов, периметра треугольника, для обучения оформлению и решению задач; способствовать развитию логического мышления учащихся
Термины и понятия		Треугольник, угол между двумя сторонами
Планируемые результаты
Предметные умения			Универсальные учебные действия
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений			Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для самостоятельной и фронтальной работы
I этап. Актуализация знаний учащихся
Цель деятельности	Совместная деятельность
Провести анализ ошибок контрольной работы	(Ф/И) 1. Сообщить результаты контрольной работы. 2. Прокомментировать основные ошибки. 3. Решить задачи, вызвавшие у учащихся наибольшие затруднения
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Повторить элементы треугольника	(Ф) При изучении темы необходимо учесть, что учащиеся имеют представление о треугольнике, его сторонах, углах и вершинах. Поэтому § 14 можно изучить в ходе выполнения следующих упражнений: 1. Начертите ∆ABC. Укажите: а) его стороны, вершины, углы; б) сторону, противолежащую A, В, С; в) между какими сторонами заключены A, В, С; г) углы, прилежащие стороне АВ, ВС, АС; д) угол, противолежащий стороне АВ, ВС, АС; е) периметр ∆АВС, если АВ = 5 см, ВС = 1 см, АС = 8 см; ж) формулу для вычисления периметра ∆АВС. 2. Решение задачи № 91 с оформлением на доске и в тетрадях учащихся. Дано:РАВС= 48 см, АС = 18 см, ВС – АВ = 4,6 см. Найти:АВ и ВС. Решение: Примем длину стороны АВ в сантиметрах за х, тогда ВС = (х + 4,6) см; 48 = АВ + АС + ВС = х + х + 4,6 + 18, отсюда: 2х = 25,4; х = 12,7. Значит, АВ = 12,7 см; ВС = 12,7 + 4,6 = 17,3 см. Ответ: 12,7 см и 17,3 см. 3. Сравнение треугольников. – Как выяснить, равны ли ∆АВС и ∆MNK? (Нужно ∆АВС наложить на ∆MNK; если они совместятся полностью, то ∆АВС= ∆MNK.) – Сравнение треугольников способом наложения – процесс не очень удобный. Нельзя ли каким-нибудь другим способом проверить, равны ли данные треугольники? (Нужно проверить, равны ли соответствующие элементы (стороны и углы) данных треугольников.) Записать на доске и в тетрадях: Если ∆ABC = ∆MNK, то АВ = MN, ВС = NK, АС = МK и А = M, В = N, C = K
III этап. Закрепление изученной темы
Цель деятельности	Задания для самостоятельной работы
Научить решать задачи на применение изученного материала	(И) 1. Учащиеся самостоятельно выполняют практическое задание № 89 (б, в). Учитель проверяет выполнение этого задания и исправляет ошибки. 2. Решение задачи № 90 (самостоятельно). 3. Решение задач (самостоятельно). 1) Дано: AB = AC = BC, AD = DC. 2) Дано: ∆ABD = ∆CBD, FAB = 160°. РАВС = 36 см, РADC = 40 см. Найти:BCD. Найти: стороны ∆ABC, ∆ADC. 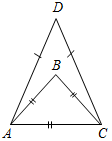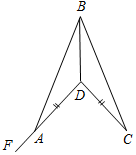Рис. 1 Рис. 2 Ответ: АВ = АС = ВС = 12 см, AD = DC = 14 см. Ответ: BCD = 20°
IV этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Что повторили на уроке? – Что нового для себя открыли?				(И) Домашнее задание: изучить п. 14 из § 1; ответить на вопросы 1 и 2 на с. 49; решить задачу № 156; выполнить практическое задание 89 (а)

---

Урок12. Первый признак равенства треугольников

Цель деятельности учителя		Создать условия для разъяснения смысла слов «теорема» и «доказательство теоремы», формулировки и доказательства первого признака равенства треугольников
Термины и понятия		Треугольник, угол между двумя сторонами, теорема, признак
Планируемые результаты
Предметные умения			Универсальные учебные действия
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений			Познавательные: выдвигают гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для самостоятельной и фронтальной работы
I этап. Актуализация знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать знания учащихся по теории	(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Повторение теории. 1) Повторить определение смежных углов и их свойство. 2) Повторить определение вертикальных углов и их свойство. 3) Вспомнить определение равных фигур, биссектрисы угла. 4) Вспомнить, какой угол называется острым, прямым, тупым. 5) Повторить определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников
II этап. Мотивация к деятельности
Цель деятельности	Задания для самостоятельной работы
Совершенствовать навыки решения задач по готовым чертежам	(И) 1. Дано: ∆АРС = ∆FMB, P = M, FB = 17 см, 2. Дано: ∆ABC = ∆ADC, ABC = 70°, A = F, PC = 23 см. AB = 10 см. Найти: AC, MB. Найти:MDC, AD. 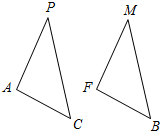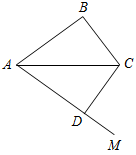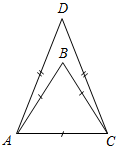Рис. 1 Рис. 2 3. Дано: АВ = ВС = AC, AD = CD, РАВС = 36 м, РАDС = 40 см. Найти: стороны ∆ABC, ∆ADC. Рис. 3
III этап. Изучение новой темы
Цель деятельности	Совместная деятельность
Вывести первый признак равенства треугольников	(Ф) Изучение темы осуществляется в форме беседы учителя с учащимися; теорему лучше доказать самому учителю. – Какие условия должны выполняться для того, чтобы ∆АВС был равен ∆А1В1С1? (АВ = А1В1, АС = А1С1, ВС = B1С1,A= А1,B = B1,C = C1.) – Нельзя ли уменьшить количество условий для доказательства равенства двух треугольников? (Учащиеся высказывают свои предположения.) – Оказывается, не нужно проверять равенство всех сторон и углов одного треугольника сторонам и углам другого треугольника. Достаточно сравнить лишь три элемента одного треугольника с тремя элементами другого. О том, какие именно элементы нужно сравнивать, нам расскажут признаки равенства треугольников. Сегодня мы изучим первый признак равенства треугольников, который гласит: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Это утверждение нам необходимо доказать. В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы. – Какие теоремы нам уже известны? (Свойство смежных углов и свойство вертикальных углов.) – Любая теорема состоит из условия и заключения. Условие – это уже известные факты, о которых говорится в теореме, а заключение – это то, что нужно получить, доказать. – Выделите условие теоремы первого признака равенства треугольников. Выделите заключение. Итак, докажем первый признак равенства треугольников: Дано (условие): ∆ABC, ∆А1В1С1, АВ = А1В1, АС = А1С1, A = A1. Доказать (заключение): ∆АВС = ∆А1В1С1. Доказательство: см. п. 15 учебника. – Первый признак равенства треугольников удобнее называть признаком равенства треугольников по двум сторонам и углу между ними
IV этап. Решение задач
Цель деятельности	Задания для самостоятельной работы
Совершенствовать навыки в решении задач на изученную тему	(Ф/И) 1. Найти пары равных треугольников: 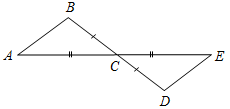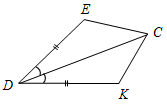Рис. 4 Рис. 5 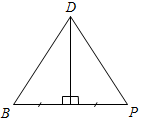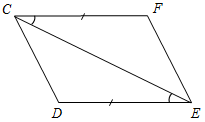Рис. 6 Рис. 7 2. Решить задачи № 96 и 97 на доске и в тетрадях
V этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Что нового узнали на уроке? – Что такое теорема? Из чего она состоит?				(И) Домашнее задание: знать доказательство первого признака равенства треугольников (п. 15), решить задачи № 93, 94 и 95

1   2   3   4   5   6   7   8   9   10   ...   47

---

Урок13. Решение задач на применение первого признака
равенства треугольников

Цель деятельности учителя		Создать условия для совершенствования навыков решения задач на применение первого признака равенства треугольников, закрепления умения доказывать теоремы
Термины и понятия		Треугольник, теорема, признак
Планируемые результаты
Предметные умения			Универсальные учебные действия
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений			Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки; устанавливают причинно-следственные связи, строят логическое рассуждение, делают умозаключения. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для фронтальной и самостоятельной работы
I этап. Актуализация знаний учащихся
Цель деятельности	Совместная деятельность
Закрепить умение доказывать теорему	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Вызвать к доске учащегося для доказательства первого признака равенства треугольников. 3. Решить задачи по готовым чертежам (устно). 4. Найти равные треугольники: 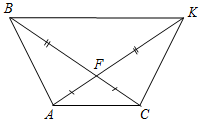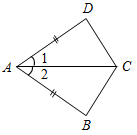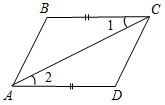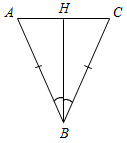Рис. 1 Рис. 2 Рис. 3 Рис. 4
II этап. Решение задач
Цель деятельности	Совместная деятельность
Cовершенствовать навыки решения задач	(Ф/И) 1. Решить задачу № 98 на доске и в тетрадях. 2. Решить задачи по готовым чертежам. Решение записать на доске и в тетрадях. 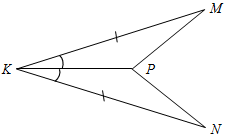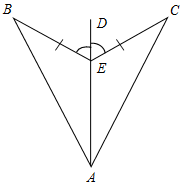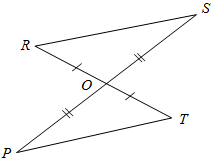Рис. 5 Рис. 6 Рис. 7
III этап. Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень усвоения теоретических знаний и умения применять их при решении задач	(И) Работа рассчитана на 10 минут. Решив ее, учащиеся сдают листки учителю. Вариант I Докажите равенство треугольников ADC и ABC, изображенных на рисунке, если AD = AB и 1 = 2. Найдите углы ADC и ACD, если АВС = 108°, АСВ = 32°. 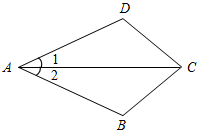Рис. 8 Вариант II Докажите равенство треугольников АВС и ADC, изображенных на рисунке 53 учебника, если АВ = DC и 4 = 3. Найдите углы АСВ и ADC, если АВС = 102°, ВСА = 38°
IV этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Что повторили на уроке? – Оцените свою работу на уроке				(И)Домашнее задание: решить № 97, 160 (а)

---

Урок14. Перпендикуляр к прямой.
Медианы, биссектрисы и высоты треугольника

Цель деятельности учителя		Создать условия для введения понятий перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника, доказательства теоремы о перпендикуляре, обучения построению медианы, биссектрисы и высоты треугольника
Термины и понятия		Треугольник, медиана, биссектриса, высота, перпендикуляр
Планируемые результаты
Предметные умения			Универсальные учебные действия
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы		Фронтальная (Ф); парная (П); индивидуальная (И)
Образовательные ресурсы		• Задания для фронтальной работы
I этап. Актуализация знаний учащихся
Цель деятельности	Совместная деятельность
Проверить правильность выполнения домашнего задания	(Ф/И) 1. Проверить правильность выполнения домашнего задания. Для этого к доске вызываются двое учеников, которые демонстрируют выполнение заданий. Остальные учащиеся задают вопросы. 2. Проанализировать ошибки, допущенные в самостоятельной работе
II этап. Учебно-исследовательская деятельность
Цель деятельности	Совместная деятельность
Ввести понятия медианы, биссектрисы и высоты треугольника в ходе практической деятельности	(Ф/И) 1. Выполнение практического задания (учитель это же задание выполняет на доске). – Начертите прямую а и отметьте точку А, не лежащую на прямой (рис. 1). 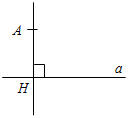Рис. 1 – Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых обозначьте Н. – Запишите в тетрадях: «Отрезок АН – перпендикуляр, проведенный из точки А к прямой а, если: 1) АНа; 2) Аа, На». Теорема о перпендикуляре:Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом только один. Дано: а – прямая, точка Аа. Доказать: 1) из точки А к прямой а можно провести перпендикуляр; 2) из точки А к прямой а можно провести единственный перпендикуляр. Доказательство: см. п. 16 учебника. 2. Определение: Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника. На доске и в тетрадях рисунок (рис. 2) и запись: AM – медиана ∆АВС, если МВС, ВМ = МС. 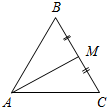Рис. 2 – Начертите ∆MNK, постройте его медианы. (На доске это же задание выполняет один из учащихся по указанию учителя.) На доске и в тетрадях рисунок (рис. 3) и запись: MB, KA, NC – медианы ∆MNK. MBKANC = О. 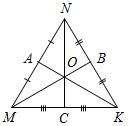Рис. 3 3. Определение:Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. На доске и в тетрадях рисунок (рис. 4) и запись: BL – биссектриса ∆АВС, если LАС, ABL = CBL. 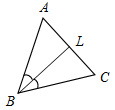Рис. 4 – Начертите ∆DEF,постройте его биссектрисы. (На доске это же задание выполняет один из учащихся по указанию учителя.) На доске и в тетрадях рисунок (рис. 5) и запись: DN, EK, FM – биссектрисы ∆DEF. DNЕKЕМ = О. 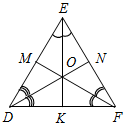Рис. 5 4.Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. На доске и в тетрадях рисунок (рис. 6) и запись: ВН – высота ∆АВС, если ВНАС, НАС. 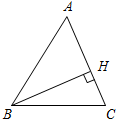Рис. 6 – Начертите остроугольный, прямоугольный и тупоугольный треугольники и постройте их высоты. 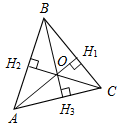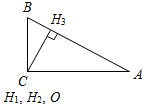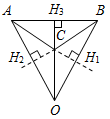Рис. 7 Рис. 8 Рис. 9 (К доске вызвать трех учеников, первый из них строит высоты для остроугольного треугольника, второй – для прямоугольного, третий – для тупоугольного.)
III этап. Решение задач на закрепление изученного материала
Цель деятельности	Деятельность учителя			Деятельность учащихся
Совершенствовать навыки построения медиан, биссектрис и высот	(П) Выполнить в парах № 101, 102, 103. (Ф/И) Выполнить на доске и в тетрадях № 105 и 106			№ 105. Дано: А, С по одну сторону от а, АВа, CDa, AB = CD, ADB = 44°. Доказать:ABD = CDB. Найти:АВС. 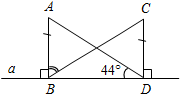Рис. 10 Доказательство: 1) В ABD и CDBBD – общая, AB = CD (по усл.). В = D = 90° (так как АВа, CDa). Таким образом, ABD = CDB (по двум сторонам и углу между ними). 2) Из п. 1 следует, что СВD = ADB = 44°, тогда АВС = ABD – CBD, АВС = 90° – 44° = 46°. № 106. Дано: АВС, AD – медиана, AD = DЕ, AСD = 56°, ABD = 40°. Доказать:ABD = ЕCD. Найти:АСЕ. 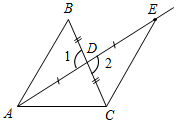Рис. 11 Доказательство: 1) Рассмотрим ABD и ЕCD. BD = DC (по усл.), AD = DE (по усл.), 1 = 2 – вертикальные, ABD = ЕCD (по двум сторонам и углу между ними), тогда ABD = ЕCD (по определению равных треугольников), ЕCD = 40°. 2) АСЕ = AСD + ЕCD = 56° + 40° = 96°
IV этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Какими свойствами обладают медианы, биссектрисы и высоты треугольника? – Составьте синквейн к уроку				(И)Домашнее задание: изучить пункты 16 и 17; ответить на вопросы 5–9 на с. 50; решить № 100

1   ...   4   5   6   7   8   9   10   11   ...   47

---

Урок15. Свойства равнобедренного треугольника

Цель деятельности учителя	Создать условия для введения понятий равнобедренного треугольника, равностороннего треугольника, рас-смотрения свойств равнобедренного треугольника и демонстрации их применения на практике
Термины и понятия	Равнобедренный треугольник, равносторонний треугольник, боковые стороны, основание, углы при основании
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания		Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение; понимают и используют математические средства наглядности. Регулятивные: осознают и принимают цели и задачи учебной деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для самостоятельной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить правильность выполнения домашнего задания	( 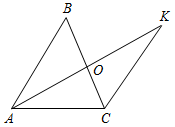Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Теоретический опрос учащихся. 3. Самостоятельное решение тестовых заданий с последующей самопроверкой: 1) Дано: АО – медиана ∆АВС, АО = ОK, АВ = 6,3 см, ВС = 6,5 см, АС = 6,7 см. Найти: СK. Рис. 1 а) 6,4 см; б) 6,7 см; в) 6,5 см; г) 6,3 см. 2) Дано: ОН и ON – высоты ∆МОK и ∆EOF, OH = ON, EN = 7,8 см, ОЕ = 8,6 см, НМ = 6,3 см. 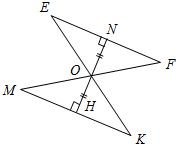Найти: МK. Рис. 2 а) 13,9 см; б) 14,1 см; в) 14,9 см; г) 16,4 см. 3) В треугольниках ABC и KРМ проведены биссектрисы ВО и РЕ, причем ∆АВО = ∆KРЕ. Найдите отрезок ЕМ, если АС = 9 см, а ЕМ больше KЕ на 3,8 см. а) 6,4 см; б) 5,4 см; в) 2,6 см; г) 4,8 см. Ответы: 1 – г; 2 – б; 3 – а
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Ввести понятия равнобедренного и равносто-роннего треугольников, дать представления о свойствах равнобедренного треугольника	(Ф/И) 1.Понятия равнобедренного и равностороннего треугольников. О 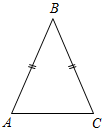пределение: Треугольник, две стороны которого равны, называется равнобедренным. Равные стороны называются боковыми сторонами, а третья сторона – основанием равнобедренного треугольника. На доске и в тетрадях учащихся – рисунок и запись: ∆АВС – равнобедренный, так как АВ = ВС; АВ, ВС – боковые стороны равнобедренного ∆АВС; АС – основание равнобедренного ∆АВС; A, C – углы при основании равнобедренного ∆ABC; B – угол при вершине равнобедренного ∆АВС. Рис. 3 Определение:Треугольник, все стороны которого равны, называется равносторонним. 2 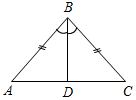. Свойство углов при основании равнобедренного треугольника. Теорема:В равнобедренном треугольнике углы при основании равны. Дано: ∆АВС, АВ = ВС. Доказать:A = C. Рис. 4 Доказательство: Проведем биссектрису из вершины В к основанию АС.(Далее можно предложить учащимся продолжить доказательство самостоятельно, заслушать варианты, обсудить и записать в кратком виде ход доказательства.) (Г) 3. Свойство биссектрисы, проведенной к основанию равнобедренного треугольника. Можно предложить учащимся вывести это свойство самостоятельно, поставив перед ними проблему: «Как известно, биссектриса треугольника делит его угол пополам. Но в равнобедренном треугольнике биссектриса, проведенная к основанию, обладает еще одним очень важным свойством. В чем заключается это свойство?» Работа проводится в группах по 3–4 человека с последующим обсуждением этого свойства с доказательством. При обсуждении важно затронуть вопросы: – Каждая ли биссектриса равнобедренного треугольника является его высотой и медианой? – Является ли высота равнобедренного треугольника его биссектрисой и медианой? Если да, то какая из трех?
III этап. Творческое задание
Цель деятельности	Задания для самостоятельной работы
Способствовать исследованию свойств медиан и высот равнобедренного треугольника в ходе выполнения заданий творческого характера	(И) Вариант I Исследуйте медианы равнобедренного треугольника и перечислите все их особенности и свойства. Вариант II Исследуйте высоты равнобедренного треугольника и перечислите все их особенности и свойства. Далее проходит обсуждение свойств медианы и высоты равнобедренного треугольника
IV этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения задач на применение изученных фактов	(Ф/И) 1. Решить задачи № 108 и 112 на доске и в тетрадях. 2. Решить № 116 (устно). 3. Решить задачу (устно). В равнобедренном треугольнике сумма всех углов равна 180º. Найдите углы этого треугольника, если известно, что: а) один из них равен 105º; б) один из них равен 38º (рассмотреть два случая)		№ 108. Дано:АВС, АВ = АС, РАВС = 40 см, ВСD, DB = DC = BC, PВCD = 45 см. Найти:ав и ВС. Рис. 5 Решение: 1) РАВС = АВ + ВС + АС = ВС + 2АВ (так как АВС равнобедренный), 4 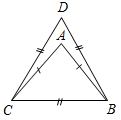0 = ВС + 2АВ. 2) PВCD = DB + ВС + CD = 3ВС (так как DВС равносторонний), 45 = 3ВС, тогда ВС = 15 см. 40 = 15 + 2АВ. 2АВ = 25, тогда АВ = 12,5 см. Ответ: 12,5 см; ВС = 15 см. № 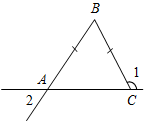112. Дано: АВ = ВС, 1 = 130°. Найти:2. Рис. 6 Решение: 1) 1 и АСВ – смежные, значит, 1 + АСВ = 180°, тогда АСВ = 180° – 130° = 50°. 2) Так как АВС – равнобедренный, АВ = ВС (по усл.), то ВАС = АСВ = 50°. 3) Так как 2 = ВАС, как вертикальные, 2 = 50°. Ответ: 50°
V этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Что узнали об углах равнобедренного треугольника? Равностороннего треугольника? – Перечислите свойства равнобедренного и равностороннего треугольников. – Задайте три вопроса по теме урока			(И) Домашнее задание: изучить п. 18 с доказательством теоремы об углах при основании равнобедренного треугольника; ответить на вопросы 10–12 на с. 50; решить задачи № 104, 107 и 117

---