Файл: Урок Прямая и отрезок.docx

Скачать файл (2,03Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 417

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Урок16. Свойства равнобедренного треугольника

Цели деятельности учителя	Создать условия для закрепления теоретических знаний по изучаемой теме; совершенствовать навыки доказательства теорем, решения задач
Термины и понятия	Равнобедренный треугольник, равносторонний треугольник, боковые стороны, основание, углы при основании
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания		Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; устанавливают причинно-следственные связи, строят логическое рассуждение, умозаключение; понимают и используют математические средства наглядности. Регулятивные: принимают и сохраняют учебные задачи. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для самостоятельной работы. • Чертежи к задачам
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить уровень сформированности теоретических знаний	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Один учащийся на доске готовит доказательство теоремы о свойстве углов при основании равнобедренного треугольника. 3. Второй учащийся решает на доске задачу № 117 (по рис. 67). 4. Устно по готовым чертежам на доске учащиеся решают задачи. – Найдите DВА. 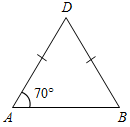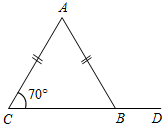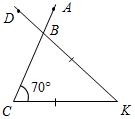Рис. 1 Рис. 2 Рис. 3 5. Теоретический тест (с последующей самопроверкой). (Ответы учащиеся записывают на двух листках, один из них сдают на проверку учителю, по другому проверяют правильность своих ответов. Ответы к тесту учитель записывает на доске после того, как учащиеся сдали работы.) 1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 2) Если треугольник равносторонний, то: а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой. 3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника? а) В любом; б) в равнобедренном; в) в равностороннем. 4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение: а) всегда верно; б) может быть верно; в) всегда неверно. 5) Если треугольник равнобедренный, то: а) он равносторонний; б) любая его медиана является биссектрисой и высотой; в) ответы а) и б) неверны. 6) В каком треугольнике любая его высота делит треугольник на два равных треугольника? а) В любом; б) в равнобедренном; в) в равностороннем. Ответы: 1 – б; 2 – а, б, в; 3 – б; 4 – а; 5 – в; 6 – в
II этап. Решение задач
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения задач	(Ф/И) 1. Решение задач по готовым чертежам. Найти угол DВА. 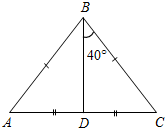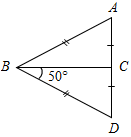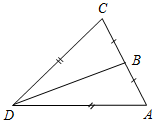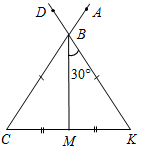Рис. 4 Рис. 5 Рис. 6 Рис. 7 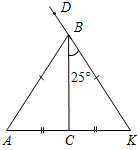Рис. 8 2. Решение № 119 и 120 (а) на доске и в тетрадях. 3. Самостоятельная работа на 10 минут. 1) Периметр равнобедренного треугольника 48 см, боковая сторона – 15 см. Найти основание треугольника. 2) Периметр равнобедренного треугольника равен 37 см. Основание меньше боковой стороны на 5 см. Найдите стороны этого треугольника
III этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Оцените свою работу на уроке. – Закончите фразы: • Я научился… • У меня получилось… • Я смог… • Я попробую…			(И) Домашнее задание: решить № 114, 118, 120 (б)

1 ... 5 6 7 8 9 10 11 12 ... 47

Урок17. Второй признак равенства треугольников

Цели деятельности учителя	Создать условия для повторения и закрепления изученного ранее материала, изучения второго признака равенства треугольников и выработки навыков использования первого и второго признаков равенства треугольников при решении задач; способствовать развитию логического мышления учащихся
Термины и понятия	Треугольник, прилежащие углы
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию)		Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Чертежи к задачам. • Задания для фронтальной и индивидуальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Совершенствовать навык решения задач по готовым чертежам с целью повторения первого признака равенства треугольников	(Ф/И) 1. Проверка домашнего задания. 2. Решение задач (устно). 1) На рис. 1 DЕ = DK, 1 =2. Найдите ЕС,DСK и DKС, если KС = 1,8 дм; DСЕ = 45º,DЕС =115º. 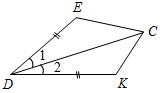Рис. 1 2) ОВ = ОС, АО = DО; АСВ = 42º, DСF = 68º. Найдите АВС. 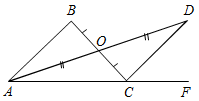Рис. 2
II этап. Изучение нового материала
Цель деятельности	Совместная деятельность
Организовать выполнение практической работы с целью подготовки к восприятию новой темы	(Ф/И) Практическая работа. Начертите MNK – такой, что ∆MNK = ∆ABC, если известно, что АВ = 4 см, A = 54°, В = 46°. Построение: 1) отложить отрезок MN = 4 см, так как ∆MNK = ∆АВС, а значит, MN = AB; 2) построить NMP = 54°; 3) построить MNE = 46° по ту же сторону от прямой MN, что и NMP; 4) МРNE = K, ∆MNK – искомый. (Идет обсуждение практического задания. Учитель задает вопросы, учащиеся отвечают на них.) – Будут ли равны ∆АВС и ∆MNK, если АВ = MN, A = M, B = N? (Да, ∆ABC = ∆MNK.) – Докажите равенство треугольников ABC и MNK. Дано: ∆ABC, ∆MNK, AB = MN, A = M, B = N. Доказать: ∆ABC = ∆MNK. Доказательство: Наложим ∆ABC на ∆MNK так, чтобы АВ совместилось с MN, а вершины С и K лежали по одну сторону от MN. Так как по условию задачи АВ = MN, то вершина А совместится с вершиной М, а вершина В – с вершиной N. Луч АС совместится с лучом МK, так как A = М, а луч ВС совместится с лучом NK, так как B = N. Точка пересечения лучей АС и ВС совместится с точкой пересечения лучей МK и NK, то есть точка С совместится с точкой K. Получили, что треугольники ABC и MNK полностью совместились, а это значит, что ∆ABC = ∆MNK. – Итак, мы только что доказали второй признак равенства треугольников. Сформулируйте его и дайте ему название. Определение: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. – Второй признак равенства треугольников можно назвать признаком равенства треугольников по стороне и прилежащим к ней углам
III этап. Решение задач на закрепление изученного материала
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения задач по изученной теме	(Ф/И) 1. Решить задачи по готовым чертежам (устно). 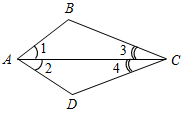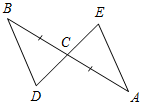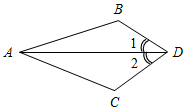Рис. 3 Рис. 4 Рис. 5 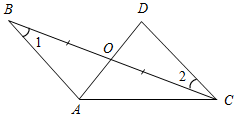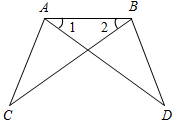Рис. 6 Рис. 7 1) На рис. 3 1 = 2 и 3 = 4. Докажите, что ∆АВС = ∆АDС. 2) На рис. 4 АС = СВ, А = В. Докажите, что ∆ВСD = ∆АСЕ. 3) На рис. 5 АD – биссектриса угла ВАС, 1 = 2. Докажите, что ∆АВD = ∆АСD. 4) На рис. 6 ВО = ОС, 1 = 2. Укажите равные треугольники на этом рисунке. 5) На рис. 7 1 = 2, САВ = DВА. Укажите равные треугольники на этом рисунке. 2. Решить задачу № 121 (самостоятельно). 3. Решить задачу № 126 (по рис. 74 учебника на с. 40). 4. Решить задачу № 127 (записать решение этой более сложной задачи на доске и в тетрадях). № 127. Дано:АВС, А₁В₁С₁, АВ = А₁В₁, ВС = В₁С₁, В = В₁; DAB, D₁A₁B₁, ACD = A₁C₁D₁. Доказать:BCD = B₁C₁D₁. Доказательство: 1) Рассмотрим АВС и А₁В₁С₁: АВ = А₁В₁(по усл.), ВС = В₁С₁(по усл.), В = В₁(по усл.), АВС = А₁В₁С₁(по двум сторонам и углу между ними), тогда AC = А₁С₁, А = А₁, С = С₁ (по определению равных треугольников). 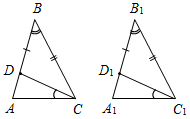Рис. 8 2) Рассмотрим BCD и B₁C₁D₁, ВС = В₁С₁, BCD = B₁C₁D₁ (так как BCD = С – ACD, B₁C₁D₁ = = С₁– A₁C₁D₁). В = В₁ (по усл.). BCD = B₁C₁D₁ (по стороне и двум прилежащим углам), что и требовалось доказать
IV этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Что нового узнали на уроке? – Кто может повторить второй признак равенства треугольников? – Составьте синквейн по теме урока			(И) Домашнее задание: выучить доказательство теоремы из п. 19; решить задачи № 124, 125, 128

1 ... 6 7 8 9 10 11 12 13 ... 47

Урок18. Второй признак равенства треугольников

Цель деятельности учителя		Совершенствовать навыки решения задач на применение второго признака равенства треугольников
Термины и понятия		Треугольник, прилежащие углы
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию)			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: осознают важность и необходимость изучения предмета
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы		• Тестовые задания
I этап. Актуализация опорных заданий учащихся
Цель деятельности	Совместная деятельность
Проверить теоретический уровень усвоения материала	(И) 1. Доказательство второго признака равенства треугольников. (К доске вызывается один из учащихся, ответ его заслушивается всем классом.) (Ф) 2. Фронтальная работа с классом – тестовые задания обучающего характера с последующей самопроверкой. 1) Для доказательства равенства треугольников ABC и MNK достаточно доказать, что: a) AC = MN; б) C = N; в) ВС = NK. 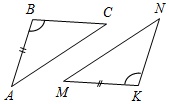Рис. 1 2) Для доказательства равенства треугольников ABC и EDF достаточно доказать, что: a) AC = FE; б) C = E; в) A = F. 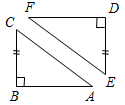Рис. 2 3) Чтобы доказать равенство равносторонних треугольников ABC и MNK, достаточно доказать, что: a) A = M; б) AB = MN; в) Р_АВС = Р_MNK. 4) Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF c основаниями TS и DF соответственно, достаточно доказать, что: a) O = E; б) TS = DF и T = D; в) TS = DF. 5) Выберите верное утверждение: a) BC = KМ; б) AB = KN; в) BC = NM. 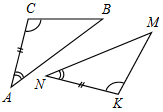Рис. 3 Ответы: 1 – в; 2 – б; 3 – б; 4 – б; 5 – а
II этап. Решение задач
Цель деятельности	Деятельность учителя				Деятельность учащихся
Совершенствовать навыки решения задач	(Г) Организует деятельность учащихся. Учащиеся распределяются в группы по 3–4 чело-века и решают задачи № 130, 131, 133, выполняя рисунки и записывая краткие решения. Учитель контролирует правильность решения задач в группах, при необходимости консультирует как целые группы, так и отдельных учащихся. Группы презентуют свои решения				№ 130. Дано:АВС и А₁В₁С₁, СО, С₁О₁ – медианы, ВС = В₁С₁, В = В₁, С = С₁. Доказать: 1) АСО = А₁С₁О₁; 2) ВСО = В₁С₁О₁. 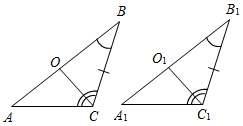Рис. 4 Доказательство: 1) Рассмотрим АВС и А₁В₁С₁. ВС = В₁С₁ (по усл.), В = В₁(по усл.), С = С₁(по усл.). АВС = А₁В₁С₁ (по сторонам и двум углам). АВ = А₁В₁, А = А₁, АС = А₁С₁ (по определению равных треугольников). 2) Рассмотрим АОС = А₁О₁С₁. АС = А₁С₁ (из п. 1), А = А₁ (из п. 1). АО = А₁С₁. АОС = А₁О₁С₁ (по двум сторонам и углу между ними). 3) Рассмотрим ВСО = В₁С₁О₁. ВС = В₁С₁ (по усл.), В = В₁(по усл.), ОВ = О₁В_{1 .} ВСО = В₁С₁О₁(по двум сторонам и углу между ними). № 131. Дано:DEF и MNP, EF = NP, DF = MP, F = P, EE₁, DD₁ – биссектрисы, EE₁DD₁ = О, ММ₁NN₁ = K. Доказать:DOE = MKN. 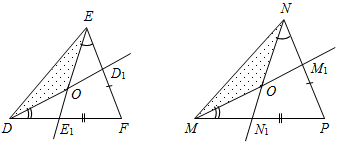Рис. 5 Доказательство: 1) Рассмотрим DEF и MNP. EF = NP (по усл.), DF = MP (по усл.),F = P (по усл.). DEF = MNP (по двум сторонам и углу между ними), тогда D = М, Е = N, DE = MN (по определению равных треугольников). 2) Рассмотрим DOE и MNK. DE = MN (из п. 1), EDO = NMK . DEO = MNK . DOE = MKN (по стороне и двум прилежащим углам), тогда DOE = MKN (по определению равных треугольников). № 133. Дано:АВС, BD – биссектриса. Доказать:АВС – равнобедренный. 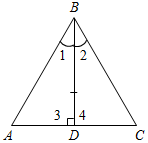Рис. 6 Доказательство: Рассмотрим ABD и CBD: BD – общая, 1 = 2 (так как BD – биссектриса), 3 = 4 (так как BD – высота). ABD = CBD (по стороне и двум прилежащим углам). АВ = ВС (по определению равных треугольников), значит, АВС – равнобедренный
III этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Оцените свою работу. – Оцените работу в группе				(И) Домашнее задание: решить 129, 132, 134

1 ... 7 8 9 10 11 12 13 14 ... 47

Урок18. Второй признак равенства треугольников

Цель деятельности учителя		Совершенствовать навыки решения задач на применение второго признака равенства треугольников
Термины и понятия		Треугольник, прилежащие углы
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию)			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: осознают важность и необходимость изучения предмета
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы		• Тестовые задания
I этап. Актуализация опорных заданий учащихся
Цель деятельности	Совместная деятельность
Проверить теоретический уровень усвоения материала	(И) 1. Доказательство второго признака равенства треугольников. (К доске вызывается один из учащихся, ответ его заслушивается всем классом.) (Ф) 2. Фронтальная работа с классом – тестовые задания обучающего характера с последующей самопроверкой. 1) Для доказательства равенства треугольников ABC и MNK достаточно доказать, что: a) AC = MN; б) C = N; в) ВС = NK. Рис. 1 2) Для доказательства равенства треугольников ABC и EDF достаточно доказать, что: a) AC = FE; б) C = E; в) A = F. Рис. 2 3) Чтобы доказать равенство равносторонних треугольников ABC и MNK, достаточно доказать, что: a) A = M; б) AB = MN; в) Р_АВС = Р_MNK. 4) Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF c основаниями TS и DF соответственно, достаточно доказать, что: a) O = E; б) TS = DF и T = D; в) TS = DF. 5) Выберите верное утверждение: a) BC = KМ; б) AB = KN; в) BC = NM. Рис. 3 Ответы: 1 – в; 2 – б; 3 – б; 4 – б; 5 – а
II этап. Решение задач
Цель деятельности	Деятельность учителя				Деятельность учащихся
Совершенствовать навыки решения задач	(Г) Организует деятельность учащихся. Учащиеся распределяются в группы по 3–4 чело-века и решают задачи № 130, 131, 133, выполняя рисунки и записывая краткие решения. Учитель контролирует правильность решения задач в группах, при необходимости консультирует как целые группы, так и отдельных учащихся. Группы презентуют свои решения				№ 130. Дано:АВС и А₁В₁С₁, СО, С₁О₁ – медианы, ВС = В₁С₁, В = В₁, С = С₁. Доказать: 1) АСО = А₁С₁О₁; 2) ВСО = В₁С₁О₁. Рис. 4 Доказательство: 1) Рассмотрим АВС и А₁В₁С₁. ВС = В₁С₁ (по усл.), В = В₁(по усл.), С = С₁(по усл.). АВС = А₁В₁С₁ (по сторонам и двум углам). АВ = А₁В₁, А = А₁, АС = А₁С₁ (по определению равных треугольников). 2) Рассмотрим АОС = А₁О₁С₁. АС = А₁С₁ (из п. 1), А = А₁ (из п. 1). АО = А₁С₁. АОС = А₁О₁С₁ (по двум сторонам и углу между ними). 3) Рассмотрим ВСО = В₁С₁О₁. ВС = В₁С₁ (по усл.), В = В₁(по усл.), ОВ = О₁В_{1 .} ВСО = В₁С₁О₁(по двум сторонам и углу между ними). № 131. Дано:DEF и MNP, EF = NP, DF = MP, F = P, EE₁, DD₁ – биссектрисы, EE₁DD₁ = О, ММ₁NN₁ = K. Доказать:DOE = MKN. Рис. 5 Доказательство: 1) Рассмотрим DEF и MNP. EF = NP (по усл.), DF = MP (по усл.),F = P (по усл.). DEF = MNP (по двум сторонам и углу между ними), тогда D = М, Е = N, DE = MN (по определению равных треугольников). 2) Рассмотрим DOE и MNK. DE = MN (из п. 1), EDO = NMK . DEO = MNK . DOE = MKN (по стороне и двум прилежащим углам), тогда DOE = MKN (по определению равных треугольников). № 133. Дано:АВС, BD – биссектриса. Доказать:АВС – равнобедренный. Рис. 6 Доказательство: Рассмотрим ABD и CBD: BD – общая, 1 = 2 (так как BD – биссектриса), 3 = 4 (так как BD – высота). ABD = CBD (по стороне и двум прилежащим углам). АВ = ВС (по определению равных треугольников), значит, АВС – равнобедренный
III этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Оцените свою работу. – Оцените работу в группе				(И) Домашнее задание: решить 129, 132, 134

1 ... 8 9 10 11 12 13 14 15 ... 47

Урок19. Третий признак равенства треугольников

Цель деятельности учителя		Создать условия для изучения третьего признака равенства треугольников и его закрепления в ходе решения задач, отработки у учащихся умения применять изученные теоремы при решении задач
Термины и понятия		Треугольник, углы, стороны
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию)			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для фронтальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить уровень сформированности теоретических знаний	(Ф/И) 1. Проверить домашнее задание. Для этого можно к доске вызвать троих учащихся. 2. У доски доказать второй признак равенства треугольников
II этап. Изучение новой темы
Цель деятельности	Задания для самостоятельной работы
Доказать третий признак равенства треугольников	(Ф) Учитель сам читает формулировку третьего признака равенства треугольников и доказывает его до рассмотрения первого случая. Доказательство первого случая можно провести в виде беседы с учащимися. Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Дано: ∆ABC, ∆А₁В₁С₁, АВ = А₁В₁, ВС = В₁С₁, АС = А₁С₁. Доказать: ∆АВС = ∆А₁В₁С₁. 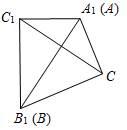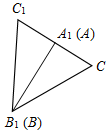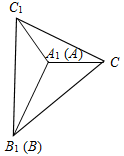Рис. 1 Рис. 2 Рис. 3 Рис. 4 Доказательство: Приложим ∆АВС к А₁В₁С₁(см. рис. 1), так чтобы сторона АВ совместилась со стороной А₁В₁ (они совместятся, так как по условию теоремы АВ = А₁В₁), а вершины С и С₁, находились по разные стороны от прямой А₁В₁. Возможны три случая: 1) луч СС₁ проходит внутри угла (рис. 2); 2) луч СС₁ совпадает с одной из сторон угла В₁С₁А₁(рис. 3); 3) луч СС₁ проходит вне угла В₁С₁А₁(рис. 4). Докажем первый случай. – Что вы можете сказать о треугольниках С₁А₁С и С₁В₁С? (Они равнобедренные.) – Равны ли углы А₁С₁В₁ и АСВ? Почему? (А₁С₁В₁ = АСВ, так как А₁С₁В₁ = A₁C₁C + B₁C₁C, ACB = = ACC₁ + BCC₁, a A₁C₁C = ACC₁, B₁C₁C = BCC₁, как углы при основании равнобедренных треугольников.) – Равны ли ∆АВС и ∆А₁В₁С₁? (∆АВС = ∆А₁В₁С₁ по двум сторонам и углу между ними, так как АС = А₁С₁, СВ = С₁В₁, ACB = A₁C₁B₁ по доказанному.) – Итак, ∆АВС = ∆А₁В₁С₁. Далее можно предложить учащимся доказать равенство треугольниковАВСиА₁В₁С₁во втором или третьем случае, а оставшийся случай рассмотреть дома. Доказательство второго случая. ∆В₁С₁С – равнобедренный с основанием СС₁, так как В₁С₁ = ВС = В₁С по условию теоремы. В₁А₁ – медиана ∆В₁С₁С, так как С₁А₁ = АС по условию теоремы, а АС = А₁С. Медиана, проведенная к основанию равнобедренного треугольника, является его биссектрисой, то есть С₁В₁А₁ = СВА. ∆АВС = ∆А₁В₁С₁ по двум сторонам и углу между ними (АВ = А₁В₁, ВС = В₁С₁ по условию теоремы, САВ = = С₁В₁А₁ по доказанному). Доказательство третьего случая. ∆В₁С₁С – равнобедренный с основанием СС₁, так как В₁С₁ = ВС по условию теоремы. B₁C₁C = ВСС₁, как углы при основании равнобедренного треугольника. ∆А₁С₁С – равнобедренный с основанием СС₁, так как А₁С = АС по условию теоремы. A₁C₁C = АСС₁, как углы при основании равнобедренного треугольника. В₁С₁А₁ = ВСА, так как В₁С₁А₁ = B₁C₁C – A₁C₁C, BCA = BCC₁ – ACC₁, a B₁C₁C = BCC₁и A₁C₁C = ACC₁ по доказанному. ∆ABC = ∆A₁B₁С, по двум сторонам и углу между ними (ВС = В₁С₁, АС = A₁C₁, ВСА = B₁C₁A₁). Далее можно ввести понятие жесткой фигуры или предложить учащимся самостоятельно прочитать с. 40 учебника – на уроке или дома
III этап. Решение задач на закрепление изученной темы
Цель деятельности	Совместная деятельность
На простых задачах отработать применение третьего признака равенства треугольников	(Ф/И) 1. Найдите пары равных треугольников и докажите их равенство. 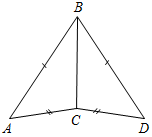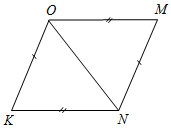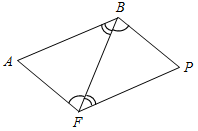Рис. 5 Рис. 6 Рис. 7 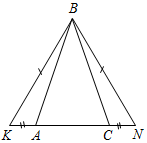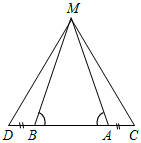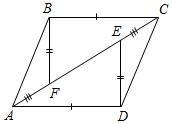Рис. 8 Рис. 9 Рис. 10 2. Решить № 135 (устно). 3. Решить № 138 на доске и в тетрадях
IV этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – С чем познакомились на уроке? – Задайте три вопроса по теме урока				(И) Домашнее задание: повторить п. 15–19, изучить п. 20; решить № 134, 136, 137