Файл: Урок Прямая и отрезок.docx

Урок 20. Решение задач

Цели деятельности учителя		Создать условия для организации и проведения повторения и закрепления изученного материала в ходе решения задач, обучения учащихся умению применять изученные теоремы при решении задач; способствовать развитию логического мышления
Термины и понятия		Треугольник, углы, стороны, признаки равенства
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию)			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для самостоятельной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Задание для контрольной работы
Систематизировать теоретические знания	(Ф/И) 1. Проверка выполнения домашнего задания. 2. Теоретический опрос. 3. Самостоятельная работа на 10–15 минут (см. Ресурсный материал). Учащиеся решают работу на листках и сдают на проверку учителю
II этап. Решение задач
Цель деятельности	Деятельность учителя			Деятельность учащихся
Совершенствовать навыки решения задач	(Ф/И) 1. Организовать решение № 139 на доске и в тетрадях. 2. Организовать решение № 169 по рисунку 95 на с. 50 на доске и в тетрадях. Рассказать учащимся о способе измерения ширины озера(отрезка АВ) по заранее изготовленной таблице: «Чтобы измерить на местности расстояние между двумя точками А и В, из которых одна (точка А) недоступна, провешивают направление отрезка АВ и на его продолжении отмеряют на земле произвольный отрезок ВС. Выбирают на местности точку О, из которой видна точка А и можно пройти к точкам В и С. Провешивают прямые ВОЕ и СОD, отмеряют на местности DО = ОС и ОЕ = = ОВ. Затем идут по прямой DЕ, глядя на точку А, пока не найдут точку F, которая лежит на прямой АО. Тогда FE равно искомому расстоянию. Расстояние FE измеряют на земле с помощью рулетки». 3. Организовать решение задачи № 176 на доске и в тетрадях			№ 139. Дано:АВ = CD, AD = BC, BE – биссектриса АВС, DF – биссектриса ADC. Доказать: 1) АВЕ = ADF; 2) АВЕ = CDF. 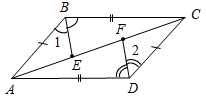Рис. 1 Доказательство: 1) Рассмотрим АВС и CDA. АВ = CD (по усл.), BC = AD (по усл.), АС – общая, АВС = CDA (по трем сторонам). В = D, ВАС = = DCA, АСВ = CAD (по определению равенства треугольников). 2) АВЕ = АВС (так как ВЕ – биссектриса). ADF = ADC (так как DF – биссектриса), тогдаАВЕ = ADF (из п. 1). 3) Рассмотрим АВЕ и СDF: АВ = CD (по усл.), ВАС = DCA (из п. 1). 1 = 2 (из пп. 1 и 2), таким образом, АВЕ = СDF (по стороне и двум прилежащим углам). № 176. Дано:АВС и А1В1С1, АВ = А1В1, АС = А1С1, АМ = А1М1; АМ, А1М1 – медианы. Доказать:АВС = А1В1С1. 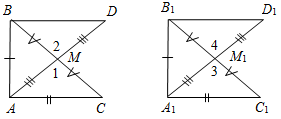Рис. 2 Доказательство: 1) Сделаем дополнительное построение: проведем АМ и А1М1 за точки М и М1 и отметим на их продолжениях точки D и D1 так, чтобы АМ = МD, А1М1 = М1D1. 2) Рассмотрим АМС и BMD. AM = MD (по постр.), BM = MC (по усл.), 1 = 2 (вертик.), АМС = BMD (по двум сторонам и углу между ними), тогда АС = BD (по определению равных треугольников), так как АС = А1С1, BD = B1D1. Рассмотрим А1М1С1 = B1M1D1. А1М1 = M1D1 (по постр.), B1M1 = М1С1 (по усл.), 3 = 4 (вертик.). А1М1С1 = B1M1D1 (по двум сторонам и углу между ними), тогда А1С1 = B1D1 (по определению равных треугольников). 3) Рассмотрим ABD и A1B1D1. АВ = А1В1 (по усл.), AD = A1D1 (так как АМ = А1М1), BD = B1D1 (из п. 2); таким образом, ABD = A1B1D1 (по трем сторонам), а значит, медианы ВМ и B1M1 этих треугольников опущены на соответственно равные стороны AD и A1D1. Так как ВМ = B1M1, то ВС = В1С1 (ВС = 2ВМ; В1С1 =2B1М1). 4) Рассмотрим АВС и А1В1С1. АВ = А1В1 (по усл.), АС = А1С1 (по усл.), ВС = В1С1 (из п. 3). Таким образом, АВС = А1В1С1 (по трем сторонам), что и требовалось доказать
III этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Перечислите признаки равенства треугольников. – Поразмышляйте на тему «Как бы мы доказывали равенство треугольников, если бы не знали признаков их равенства?»				(И) Домашнее задание: повторить пункты 16–20 из § 2 и 3; решить задачи № 140, 172. Дополнительная задача: Два равнобедренных треугольника АВС и ADC имеют общее основание АС. Вершины В и D расположены по разные стороны от АС. Точка Е лежит на отрезке BD, но не лежит на отрезке АС. Докажите, что EAC = АСЕ

---

Ресурсный материал

Самостоятельная работа

В 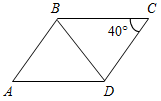ариант I

1. Дано: АВ = CD, BC = DA, С = 40°.

Доказать: ∆ABD = ∆CDB.

Найти:A.

2. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника.

Докажите, что MD = ND.

Вариант II

1 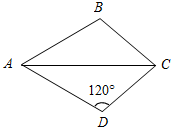. Дано:AD = AB, CD = CB, D = 120°.

Доказать: ∆DAC = ∆BAC.

Найти:В.

2. На боковых сторонах равнобедренного треугольника ABC отложены равные отрезки ВМ и BN. BD – высота треугольника.

Докажите, что MD = ND.

Урок 21. Задачи на построение. Окружность

Цель деятельности учителя	Создать условия для систематизации знаний об окружности и ее элементах, для отработки навыков решения задач по данной теме
Термины и понятия	Окружность, центр, радиус, диаметр, хорда
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют формулировать определение окружности, объяснять, что такое центр, радиус, диаметр, хорда окружности		Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для теста
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить правильность выполнения домашнего задания	(Ф/И) 1. Сообщить результаты самостоятельной работы. 2. Проверить правильность выполнения домашнего задания
II этап. Учебно-познавательная деятельность
Цель деятельности	Задания для самостоятельной работы
Ввести понятия окружности и ее элементов	(И) Понятие окружности и ее элементов вводится в курсе математики пятого класса, поэтому изучение нового материала можно организовать следующим образом: 1. Прочитать самостоятельно § 21. 2. Выполнить задания теста (см. Ресурсный материал). (На каждую парту раздаются листки с тестовым заданием. Учитель читает задание, учащиеся предлагают верный ответ.)
III этап. Закрепление изученного материала
Цель деятельности	Совместная деятельность
Отработать навыки решения задач по изученной теме	(Ф/И) 1. Решить задачу № 143 (устно). 2. Решить задачу № 144 на доске и в тетрадях. 3. Решить задачу № 146 на доске и в тетрадях. 4. Решить задачу № 147 на доске и в тетрадях. Указание: рекомендовать учащимся после изображения окружности начертить прямой угол с вершиной в точке О – центре этой окружности, а затем отметить на окружности точки А и В пересечения сторон прямого угла с окружностью
IV этап. Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень усвоения теоретического материала и умения его применять при решении задач	(И) Вариант I Отрезки KМ и ЕF являются диаметрами окружности с центром О. Докажите, что: а) FEM = KМЕ; б) отрезки KЕ и МF равны. Вариант II Отрезки МЕ и РK являются диаметрами окружности с центром О. Докажите, что: а) EMР = МРK; б) отрезки МK и РЕ равны. Вариант III В окружности с центром О проведены диаметр АС и радиус ОВ так, что хорда ВС равна радиусу. Найти АОВ, если ВСО = 60°. Вариант IV В окружности с центром О проведены хорды АВ и СD. Докажите, что АВ = СD, если АОС = ВОD
V этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Дайте определение окружности. – Перечислите все элементы окружности. – Составьте синквейн к уроку			(И) Домашнее задание: изучить п. 21 из § 4; ответить на вопрос 16 на с. 49; решить задачи № 145, 162; принести на следующий урок циркули и линейки. Дополнительная задача: АВ и CD – два диаметра окружности с центром в точке О. Луч ОЕ – биссектриса угла АОС. ОЕ пересекает окружность в точке K, причем KЕ = KО. Периметр треугольника KСО в три раза больше радиуса окружности. Докажите, что точки Е, А, С и О лежат на одной окружности

---

Ресурсный материал

---

Тест

1) Вычеркнуть ненужные слова текста в скобках.

а) Окружность – это (абстрактная, геометрическая, плоская) фигура, состоящая из (множества, всех) точек, расположенных на (одинаковом, заданном) расстоянии от (некоторой, центральной) точки.

б) Радиусом окружности называется (линия, прямая, отрезок), соединяющая центр окружности с (заданной, какой-либо) точкой окружности.

2) Закончить определение: диаметр окружности – это...

а) два радиуса, лежащие на одной прямой;

б) хорда, проходящая через центр окружности;

в) прямая, проходящая через две точки и центр окружности.

3) Закончить определение: центр окружности – это...

а) точка, куда ставится ножка циркуля при начертании окружности;

б) середина окружности;

в) точка, равноудаленная от всех точек окружности.

4) Закончить определение: дуга окружности – это...

а) часть окружности, выделенная точками;

б) часть окружности, ограниченная двумя точками;

в) часть окружности, ограниченная хордой.

5) Определить, на сколько дуг делят окружность две точки, лежащие на окружности:

а) на одну; б) на две.

6) Как изображается хорда на чертеже окружности? Выбрать правильный ответ:

а) прямой линией;

б) дугой окружности;

в) отрезком с концами, лежащими на окружности.

7) Как называется отрезок, соединяющий центр окружности с любой точкой окружности? Выбрать правильный ответ:

а) длина окружности;

б) радиус окружности;

в) половина диаметра окружности.

8) Найти на рисунке:

а) хорду (рис. 1);

б) диаметр (рис. 2).



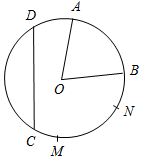
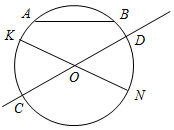
Рис. 1 Рис. 2


Урок22. Задачи на построение

Цель деятельности учителя	Создать условия для формирования представления о новом классе задач – на построение геометрических фигур с помощью циркуля и линейки без масштабных делений, для рассмотрения основных (простейших) задач этого типа
Термины и понятия	Окружность, центр, радиус, диаметр, хорда, дуга окружности, перпендикуляр, биссектриса, отрезок, угол
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют решать простейшие задачи на построение		Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для фронтальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить правильность выполнения домашнего задания	(Ф/И) 1. Сообщить результаты самостоятельной работы и проанализировать основные ошибки. 2. Проверить решение дополнительной задачи. Д 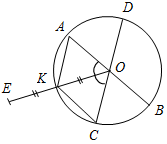оказательство: 1) ∆ОKА= ∆ОKС по двум сторонам и углу между ними (ОА = ОС, как радиусы одной окружности; ОK – общая сторона; AOK = СОK, так как ОЕ – биссектриса угла АОС). Отсюда KА = KС. 2) По условию задачи РKСО = 3R, где R – радиус окружности. ОK = R, ОС = R, следовательно, KС = R. 3) По условию задачи KЕ = KО, а так как KО = R, то KЕ = R. По доказанному KС = R,но KС = АK, следовательно, АK = R. Итак, получили, что KО = R, KE = R, KA = R, KC = R, то есть точки Е, А, С и О равноудалены от точки K и лежат на одной окружности
II этап. Беседа
Цель деятельности	Совместная деятельность
Ознакомить с этапами задачи на построение	(Ф/И) – Мы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, чертили углы, треугольники и другие фигуры с помощью различных инструментов. При построении отрезка заданной длины использовалась линейка с миллиметровыми делениями, а при построении угла заданной градусной меры – транспортир. Но, оказывается, многие построения в геометрии могут быть выполнены с помощью только циркуля и линейки без делений. В дальнейшем, говоря о задачах на построение, мы будем иметь в виду именно такие построения. Задачи на построение с помощью циркуля и линейки являются традиционным материалом, изучаемым в курсе планиметрии. Обычно эти задачи решаются по схеме, состоящей из четырех частей (см. с. 95–96 учебника). Сначала рисуют (чертят) искомую фигуру и устанавливают связи между данными задачи и искомыми элементами. Эта часть решения называется анализом. Она дает возможность составить план решения задачи. Затем по намеченному плану выполняется построение с помощью циркуля и линейки. После этого нужно доказать, что построенная фигура удовлетворяет условиям задачи. И наконец, необходимо исследовать, при любых ли данных задача имеет решение и если имеет, то сколько решений. В тех случаях когда задача достаточно простая, отдельные части, например анализ или исследование, можно опустить. В 7 классе мы будем решать простейшие задачи на построение с помощью циркуля и линейки
III этап. Задачи на построение
Цель деятельности	Совместная деятельность
Отработать навыки решения задач на построение	(Г) Разделить весь класс на шесть групп, каждая из которых готовит решение одной из задач на построение по учебнику в течение 3–5 минут. Далее по одному выходят представители групп и демонстрируют решение задач, в это время все остальные учащиеся работают в тетрадях. 1) На данном луче от его начала отложить отрезок, равный данному (§ 22). 2) Отложить от данного луча угол, равный данному (§ 23). 3) Построить биссектрису данного угла (§ 23). 4) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка (§ 23). 5) Построить середину данного отрезка (§ 23). 6) Через точку, не лежащую на прямой, построить прямую, перпендикулярную данной (задача № 153)
IV этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Из каких этапов состоит решение любой задачи на построение? – Перечислите задачи на построение. – Оцените свою работу на уроке			(И) Домашнее задание: ответить на вопросы 17–21 на с. 49; решить задачи № 149, 154; повторить материал пунктов 11–21. Найти примеры задач на построение, которые нельзя решить только с помощью циркуля и линейки

---

Урок23. Задачи на построение

Цель деятельности учителя		Создать условия для закрепления у учащихся навыков решения простейших задач на построение, для обучения решению задач на построение
Термины и понятия		Окружность, центр, радиус, диаметр, хорда, дуга окружности, перпендикуляр, биссектриса, отрезок, угол
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют решать простейшие задачи на построение			Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для индивидуальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Задания для индивидуальной работы
Проверить уровень сформированности теоретических знаний по теме	(И) Проверка усвоения теоретического материала (можно осуществить по вариантам). 1-й вариант: на данном луче от его начала отложить отрезок, равный данному. 2-й вариант: отложить от данного луча угол, равный данному. 3-й вариант: построить биссектрису данного угла. 4-й вариант: построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка. 5-й вариант: построить середину данного отрезка. 6-й вариант: через точку, не лежащую на прямой, построить прямую, перпендикулярную данной
II этап. Решение задач
Цель деятельности	Деятельность учителя			Деятельность учащихся
Отработать практичес-кие навыки решения задач на построение	(Ф/И) Организует деятельность учащихся: 1. Решить задачу № 150. 2. Решить задачи № 148, 151, 155			№ 150. Построить:МОкр. (О; r), такую, чтобы АМ = PQ. 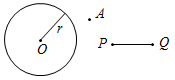Возможны 3 случая: 1) 2) 3) 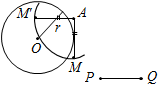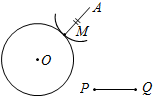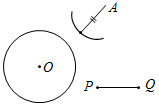AM = PQ, AM = PQ. MA = PQ. Нет решения. (2 точки) (1 точка) № 148. АВа, ВС = 2АВ. № 151. Построение: 1) С помощью циркуля построим YXQ, равныйВАС. 2) От луча XQ с помощью циркуля отложим QXZ, равный ВАС. 3) Получим YXZ = 2ВАС, что и требовалось построить. 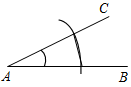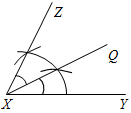Построение: 1) С помощью треугольника построим АОВ = 90°. 2) Построим биссектрису ОЕ, получили АОЕ = ВОЕ = 45°. 3) Построим OF – биссектрису АОЕ, получим АOF = ЕОF = 22°30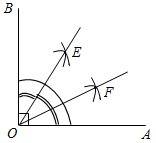
III этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Зачем необходимо уметь решать задачи на построение?				(И) Домашнее задание: написать эссе на тему «Для чего мне нужно уметь строить…»

---