Файл: Урок Прямая и отрезок.docx

Урок24. Решение задач

Цель деятельности учителя		Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, на построение с помощью циркуля и линейки
Термины и понятия		Треугольники, окружность, дуга окружности
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют применять изученные понятия, методы для решения задач практического характера			Познавательные: умеют выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: умеют самостоятельно ставить цели, понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Задания для письменной работы. • Чертежи к задачам
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить выполнение домашнего задания	(Ф/И) 1. Проверка домашнего задания. 2.Понятие трисекции угла. – Трисекция угла – задача о делении заданного угла на три равные части построением с помощью циркуля и линейки. Иначе говоря, необходимо построить трисектрисы угла – лучи, делящие угол на три равные части. Наряду с задачами о квадратуре круга и удвоении куба трисекция угла является одной из классических неразрешимых задач на построение, известных со времен Древней Греции. 3. Письменная работа на проверку навыков решения задач на построение с помощью циркуля и линейки. Вариант I 1) Отложить от данного луча угол, равный данному. 2) Построить середину данного отрезка. Вариант II 1) Построить биссектрису данного неразвернутого угла. 2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка
II этап. Решение задач
Цель деятельности	Деятельность учителя			Деятельность учащихся
Совершенствовать навыки решения задач	(Ф/И) Организует деятельность уча- щихся. 1. Решение задач по готовым чертежам. 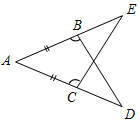Рис. 1 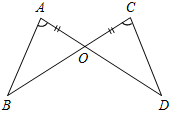Рис. 2 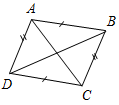Рис. 3 1) Рис. 1. а) Дано: АВ = АС, ACE = ABD. Доказать: ∆АСЕ = ∆ABD. б) Дано:АЕ = 15 см, ЕС = 10 см, АС = 1 см. Найти: стороны ∆ABD. 2) Рис. 2. Дано: АО = ОС, ВАО = DCO. Доказать: АВ = CD. 3) Рис. 3. Дано:АВ = DC, AD = ВС, РАВС = 15 см, РАВСD= 20 см. Найти: АС. 2. Решение задач № 152 и 165 на доске и в тетрадях			№ 152. Построение: 1) Построим окружность с центром О и произвольным радиусом. Окружность пересечет стороны угла в точках М и N. 2) Построим 2 окружности с одинаковым радиусом больше половины длины отрезка МN. Одна окружность с центром М, а другая с центром N. Эти окружности пересекутся в точке K. 3) Соединим лучом О и K – это и есть искомый луч, который разделил АОВ на АОХ и ВОХ. 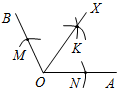Рис. 4 № 165. Дано: АВCD = О. АО = ОВ, СО = ОD, KAC, K1BD, AK = BK1. Доказать: a) OK = OK1; б) ОKK1. 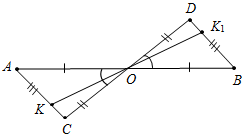Рис. 5 Доказательство: 1) Рассмотрим АОС и ВОD. АО = ОВ (по усл.), СО = ОD (по усл.), АОС = ВОD (вертикальные), АОС = ВОD (по двум сторонам и углу между ними), тогда А = В (по определению равных тре-угольников). 2) Рассмотрим AKO и BK1O. AK = BK1(по усл.), А = В (из п. 1), AKO и BK1O (по двум сторонам и углу между ними), тогда AOK = = BOK1, KO = OK (по определению равных треугольников). 3) АВ – отрезок по условию. AOK = BOK1 (из п. 2), тогда AOK и BOK1 – вертикальные, значит О, K, K1 лежат на одной прямой
III этап. Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень сформированности теоретических знаний	(И) Работа выполняется на листках и сдается на проверку учителю. Вариант I 1. На рисунке АВ = АС и ACE = ABD. 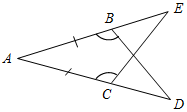Рис. 6 1) Докажите, что ACE = ABD. 2) Найдите стороны треугольника ABD, если АЕ = 15 см, ЕС = 10 см, АС = 7 см. 2. Известно, что в треугольниках АВС и А1В1С1А = А1, АВ = А1В1, АС = А1С1. На сторонах ВС и В1С1 отмечены точки K и K1, такие, что CK = C1K1. Докажите, что ABK = A1B1K1. Вариант II 1. На рисунке АО = СО и ВАО = DСО. 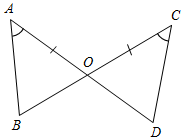Рис. 7 1) Докажите, что AОВ = DСО. 2) Найдите углы AОВ, если ОСD = 37°, ОDС = 63°, СОD = 80°. 2. Известно, что в треугольниках АВС и А1В1С1В = В1, АВ = А1В1 и ВС = В1С1. На сторонах АС и А1С1 отмечены точки D и D1, так что АD = А1D1. Докажите, что ВDС = В1D1С1
IV этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Что повторили на уроке? – Оцените свою работу на уроке				(И) Домашнее задание: повторить материал п. 15–20; решить № 158, 166

---

Урок25. Решение задач

Цель деятельности учителя	Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, проверки знаний учащихся, подготовки учащихся к предстоящей контрольной работе
Термины и понятия	Треугольники, окружность
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, результаты, методы для решения задач практического характера		Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Карточки для устного опроса. • Задачи для фронтальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить уровень сформированности теоретических знаний	(И) 1.Анализ и сообщение результатов самостоятельной работы. 2. Устный опрос учащихся у доски по карточкам (см. Ресурсный материал)
II этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения задач	(Ф/И) Организует деятельность учащихся. 1. Решить задачу. В равнобедренном треугольнике МDK длина основания МK относится к длине боковой стороны МD как 3 : 4. Найдите стороны этого треугольника, если периметр его равен 33 см. 2. Решить задачу самостоятельно. В равнобедренном треугольнике длина боковой стороны относится к длине основания как 2 : 3. Найдите стороны треугольника, если периметр его равен 28 см. (Г) 3. Решить № 175 с вынесением решения на доску и обсуждением. Описание способа построения биссектрисы угла с опорой на данную задачу. 1) Построить окружность с центром в вершине угла произвольного радиуса. Окружность пересечет стороны угла в точках А и В. 2) Построить окружности с центрами в точках А и В также произвольного радиуса. Окружность с центром А и радиусом R пересечет сторону угла в точке С, аналогично, окружность с центром В и радиусом R пересечет сторону угла в точке D. 3) Построим отрезки АD = ВС. 4) Отрезки пересекутся в точке Е. 5) Соединим лучом вершину угла с точкой Е. Получим луч ОЕ – искомая биссектриса		1. Решение: Пусть на одну часть приходится х см, тогда МK = 3х см, МD = DK = 4х см. По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3. МK = 9 см, МD = DK = 12 см. Ответ: 9 см; 12 см; 12 см. 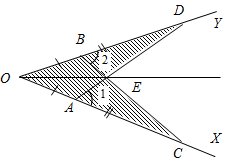№ 175. Дано: ОА = ОВ, АС = BD. Доказать: ОЕ – биссектриса. Доказательство: 1) Рассмотрим AOD и BCO. О – общий, ОА = ОВ (по усл.), ОD = ОС (так как ОD = ОВ + BD  ОС = ОА + АС). ADO = ВСО (по двум сторонам и углу между ними), тогда D = С, OAD = ОВС (по определению равных треуголь- ников). 2) OAD и 1 – смежные, значит, 1 = 180° – OAD. ОВС и 2 – смежные, значит, 2 = 180° – ОВС, тогда 1 = 2. 3) Рассмотрим BЕD и АЕС. 1 = 2 (из п. 2), D = С (из п. 1), BD = АС (по усл.), BЕD = АЕС (по стороне и двум прилежащим углам), тогда DЕ = ЕС (по определению равных треугольников). 4) Рассмотрим OЕD и ОСЕ. ОЕ – общая, ОD = ОС (из п. 1), DЕ = ЕС (из п. 3), значит, OЕD = ОЕС (по трем сторонам), тогда DOЕ = СОЕ (по определению равных треугольников), значит, ОЕ – биссектриса, что требовалось доказать
III этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Оцените свою работу на уроке. – Оцените свою работу в группе			(И) Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 15–23; решить задачи № 170, 171

1   ...   12   13   14   15   16   17   18   19   ...   47

---

Ресурсный материал

Карточки для устного опроса

Вариант I

1. Сформулируйте первый признак равенства треугольников.

2. На рисунке 1 АВ = DВ, 1 = 2. Докажите, что ∆АВС = ∆DВС.

3. В треугольниках АВС и А₁В₁С₁АВ = А₁В₁, АС = А₁С₁, А = А₁. На сторонах АС и А₁С₁ отмечены точки D и D₁ так, что СD = С₁D₁. Докажите, что ∆АВD = ∆А₁В₁D₁.

Вариант II

1. Сформулируйте второй признак равенства треугольников.

2. На рисунке 2 1 = 2, 3 = 4. Докажите, что ∆АВD = ∆СВD.

3. В треугольниках АВС и А₁В₁С₁ проведены биссектрисы АD и А₁D₁. Докажите, что ∆АВС = ∆А₁В₁С₁, если DС = = D₁С₁, С = С₁, АDС = А₁D₁С₁.

Вариант III

1. Сформулируйте третий признак равенства треугольников.

2. На рисунке 3 АВ = DС, ВС = АD. Докажите, что ∆АВС = ∆СDА.

3. На рисунке 4 АВ = DС, ВK = DМ, АМ = СK. Докажите, что ∆АDМ = ∆СВK.

Вариант IV

1. Сформулируйте свойство углов равнобедренного треугольника.

2. На рисунке 5 АВ = ВС, АD = DС. Докажите, что ∆ВАD = ∆ВСD.

3. В равнобедренном треугольнике АВС на основании АС взяты точки D и Е так, что АD = СЕ. Докажите, что треугольник DВЕ равнобедренный.

Вариант V

1. Сформулируйте свойство биссектрисы, проведенной к основанию равнобедренного треугольника.

2. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВD, АВD = 37°, АС = 25 см. Найдите В,ВDС и DС.

3. В равнобедренном треугольнике СDЕ с основанием DЕ проведена биссектриса СF. Найдите СF, если периметр треугольника СDЕ равен 84 см, а периметр треугольника СFE равен 56 см.

---

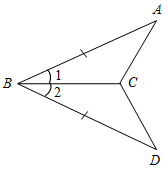
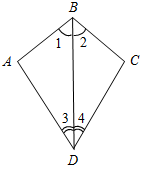
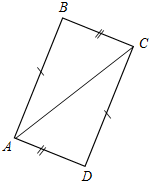
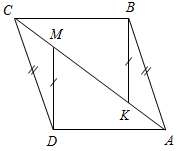
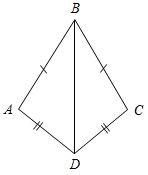
Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5

\

Урок26. Решение задач. Подготовка к контрольной работе

Цель деятельности учителя	Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, для проверки знаний учащихся, подготовки к предстоящей контрольной работе
Термины и понятия	Треугольники, окружность
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, методы для решения задач практического характера		Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Чертежи к заданиям
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Повторить признаки равенства треугольников	(Ф/И) 1. Обсудить вопросы учащихся по домашнему заданию. 2. Выполнить задание. Равносторонний треугольник изображен на рисунке… 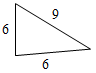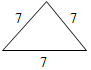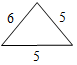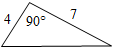а)б)в)г) 3. Выполнить задание. 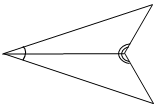Треугольники, изображенные на рисунке… а) равны по двум сторонам и углу между ними; б) равны по стороне и двум прилежащим к ней углам; в) равны по трем сторонам; г) не равны
II этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения задач	(Ф/И) Организует деятельность учащихся: решение задач № 177, 178, 179 на доске и в тетрадях		№ 177. Дано:AВC, A1В1C1, АВ = А1В1, АС = А1С1, А = А1, KАС, LВС, K1А1С1, L1В1С1, АK = А1K1, LС = L1С1. Д 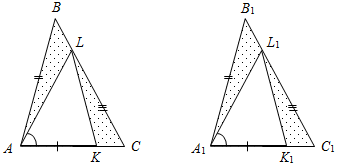оказать: а) KL = K1L1; б) AL = A1L1. Рис. 1 Доказательство: 1) Рассмотрим AВC и A1В1C1. АВ = А1В1 (по усл.), АС = А1С1 (по усл.), А = А1 (по усл.), AВC = A1В1C1 (по двум сторонам и углу между ними), тогда В = В1, С = С1, ВС = В1С1 (по определению равных треугольников). 2) Рассмотрим LСK и L1С1K1, LС = L1С1 (по усл.), С = С1 (из п. 1), KC = C1K1 (так как KC = АС – АK  K1C1 = А1С1 – А1K1). LСK = L1С1K1 (по двум сторонам и углу между ними), тогда LK = L1K1 (по определению равных треугольников). 3) Рассмотрим ABL и A1B1L1, АВ = А1В1 (по усл.), В = В1 (из п. 1), BL = B1L1 (так как BL = ВС – LС  B1L1 = B1С1 – L1C1). ABL = A1B1L1 (по двум сторонам и углу между ними), тогда AL = A1L1 (по определению равных треугольников), что и требовалось доказать. № 178. Д 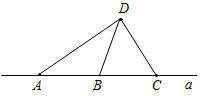ано: А, В, Са, Dа. Доказать: по крайней мере, два из трех отрезков AD, BD и CD не равны друг другу. Рис. 2 Доказательство: 1) Предположим, что AD = BD = CD. 2) Следовательно, AВD, BDC и ADC – равнобедренные, значит, 1 = 2, 3 = 4, 1 = 4. Из всех трех равенств следует, что 2 = 3, а так как 2, 3 – смежные, то 2 = 3 = 90°, следовательно, получим в AВD: А = В = 90°, в BCD: В = С = 90°, в ADC: А = С = 90°. 3) Это противоречит теореме о том, что через точку, не лежащую на прямой, можно провести единственный перпендикуляр к данной прямой, а у нас получилось 3. 4) Вывод: наше предположение неверно, следовательно, по крайней мере, два из трех отрезков AD, BD и CD не равны друг другу, что и требовалось доказать. № 179. Дано:AВC, АВ = АС, РАВ, QАС, ХВС, ВХ = ХС, РХВ = QXC. Доказать: BQ = CP. Рис. 3 Доказательство: 1) Так как AВC – равнобедренный, В = С. 2 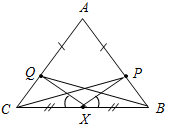) Рассмотрим CQX иBPX. СХ = ВХ (по усл.), QXC = РХВ (по усл.), С = В (из п. 1). CQX =BPX (по стороне и двум прилежащим углам), тогда CQ = РВ, QX = ХР (по определению равных треугольников). 3) Рассмотрим CQВ и ВРС. CQ = РВ (из п. 2), СВ – общая, С = В (из п. 1), СОВ = ВРС (по двум сторонам и углу между ними), тогда QB = CP, что и требовалось доказать
III этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Какие трудности у вас возникали в процессе решения задач? – Составьте синквейн к уроку				(И) Домашнее задание: решить № 180, 182, 184

---

Урок27. Контрольная работа № 2

Цель деятельности учителя	Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала
Термины и понятия	Признаки равенства треугольников, равнобедренный треугольник, равносторонний треугольник, медианы, биссектрисы, высоты треугольника
Планируемые результаты
Предметные умения			Универсальные учебные действия
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности			Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для контрольной работы
I этап. Выполнение контрольной работы
Цель деятельности		Задания для контрольной работы
Проверить уровень знаний, умений и навыков по изученному материалу		(И) Учащиеся выполняют задания контрольной работы (см. Ресурсный материал)
II этап. Итоги урока. Рефлексия
Деятельность учителя				Деятельность учащихся
(Ф/И) – Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке?				(И) Домашнее задание: повторить материал пунктов 2–21

1   ...   13   14   15   16   17   18   19   20   ...   47

---