ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 425
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Р
 есурсный материал
есурсный материалКонтрольная работа
Вариант I
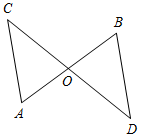
1. Дано: АО = ВО, СО = DO, СО = 5 см, ВО = 3 см, BD = 4 см (рис. 1).
Найти: периметр ∆САО.
Рис. 1
2. В равнобедренном треугольнике АВС точки K и М являются серединами боковых сторон АВ и ВС соответственно. BD – медиана треугольника. Докажите, что ∆BKD = ∆BMD.
3. Даны неразвернутый угол и отрезок. На сторонах данного угла постройте точки, удаленные от вершины угла на расстояние, равное половине данного отрезка.
4*. Прямая МK разбивает плоскость на две полуплоскости. Из точек М и K в разные полуплоскости проведены равные отрезки МА и KB, причем АМK = ВKМ. Какие из высказываний верные?
а
 ) ∆АМВ = ∆АKВ; б) AKM = BMK; в) ∆МKА = ∆KМВ; г) AMB = KМВ.
) ∆АМВ = ∆АKВ; б) AKM = BMK; в) ∆МKА = ∆KМВ; г) AMB = KМВ. Вариант II
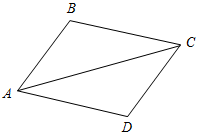
1. Дано: АВ = CD, BC = AD, AC = 1 см, AD = 6 см, АВ = 4 см (рис. 2).
Найти: периметр ∆ADC.
Рис. 2
2. В равнобедренном треугольнике АВС точки K и М являются серединами боковых сторон АВ и ВС соответственно. BD – медиана треугольника. Докажите, что ∆AKD = ∆CMD.
3. Даны неразвернутый угол и отрезок. На биссектрисе данного угла постройте точку, удаленную от вершины угла на расстояние, равное данному отрезку.
4*. Прямая АВ разбивает плоскость на две полуплоскости. Из точек А и Вв разные полуплоскости проведены равные отрезки AD и ВС, причем BAD = ABC. Какие из высказываний верные?
a) ∆CAD = ∆BDA; б) DBA = CAB; в) BAD = BAC; г) ADB = BCA.
Урок28. Работа над ошибками
| Цели деятельности учителя | Создать условия для устранения пробелов в знаниях учащихся; совершенствовать навыки решения задач по теме «Треугольники» | ||
| Термины и понятия | Треугольники, окружность | ||
| Планируемые результаты | |||
| Предметные умения | Универсальные учебные действия | ||
| Умеют применять изученные понятия, результаты, методы для решения задач практического характера | Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений | ||
| Организация пространства | |||
| Формы работы | Фронтальная (Ф); парная (П); индивидуальная (И) | ||
| Образовательные ресурсы | • Задания для парной работы | ||
| I этап. Актуализация опорных знаний учащихся | |||
| Цель деятельности | Совместная деятельность | ||
| Проанализировать затруднения, возникшие при решении контрольной работы | (Ф/И) 1. Сообщить учащимся результаты контрольной работы. 2. Решить задачи, вызвавшие наибольшее затруднение | ||
| II этап. Решение задач | |||
| Цель деятельности | Совместная деятельность | ||
| Совершенствовать навыки решения задач | (П) Учащимся предлагается решить любые три задачи из представленных. Учитель выступает в роли консуль- танта. Задача 1. В равнобедренном треугольнике ABC с основанием АС проведены медианы АЕ и CD. Докажите, что: а) ∆АВЕ = ∆CBD; б) ∆DOE и ∆АОС – равнобедренные (О – точка пересечения АЕ и CD); в) ОВ – биссектриса DOE. Задача 2. В равнобедренном ∆АВС с основанием АС на сторонах АВ и ВС отмечены соответственно точки М и N так, что ACM = CAN. Докажите, что: а) ∆MBN – равнобедренный; б) ВОMN (О – точка пересечения AN и CM). Задача 3. Треугольники АВС и DEF – равнобедренные и равные. Найти периметр ∆АВС, если DE = 4 см, EF = 5 см. Задача 4. Дано: АВ = АМ, АС = АK, ВАK = САМ. Перечислите все пары равных треугольников с вершинами в точках А, В, K, С, М. Задача 5. Н 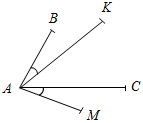 а боковых сторонах равнобедренного треугольника во внешнюю сторону построены равносторонние треугольники. а боковых сторонах равнобедренного треугольника во внешнюю сторону построены равносторонние треугольники. Докажите, что отрезки, соединяющие вершины равносторонних треугольников (отличные от вершин равнобедренного) с серединой основания равнобедренного треугольника, равны между собой | ||
| III этап. Итоги урока. Рефлексия | |||
| Деятельность учителя | Деятельность учащихся | ||
| (Ф/И) – В чем возникли затруднения? Почему? – Оцените свою работу и работу своего напарника | (И) Домашнее задание: решить оставшиеся задачи | ||
Урок29. Определение параллельных прямых.
Признаки параллельности двух прямых
| Цель деятельности учителя | Создать условия для введения понятия параллельных прямых, рассмотрения признака параллельности двух прямых, связанного с накрест лежащими углами | |||
| Термины и понятия | Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы | |||
| Планируемые результаты | ||||
| Предметные умения | Универсальные учебные действия | |||
| Владеют базовым понятийным аппаратом по основным разделам содержания | Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений | |||
| Организация пространства | ||||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |||
| Образовательные ресурсы | • Тест. • Задания для фронтальной работы | |||
| I этап. Актуализация опорных знаний учащихся | ||||
| Цель деятельности | Совместная деятельность | |||
| Проанализировать ошибки, допущенные в контрольной работе | (Ф/И) 1. Указать ошибки, допущенные учащимися при выполнении работы. 2. Решить задачи, вызвавшие затруднения у учащихся | |||
| II этап. Учебно-познавательная деятельность | ||||
| Цель деятельности | Совместная деятельность | |||
| Ввести понятие параллельных прямых, накрест лежащих углов, соответственных, односторонних углов | (Ф/И) 1. Тест (см. Ресурсный материал). Учащиеся решают задания самостоятельно. Важно подчеркнуть, что за данный тест оценки в журнал выставлены не будут; это обеспечит практически полную самостоятельность учащихся при выполнении задания. 2 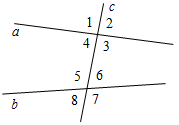 . Изучение новых понятий. . Изучение новых понятий.– Начертите прямые а и b и прямую с так, чтобы а и b пересекались с прямой с. – Сколько неразвернутых углов изображено на рисунке? Рис. 1 – Запишите в тетрадях: с – секущая по отношению к прямым а и b. 3 и 5; 4 и 6 – накрест лежащие углы. 4 и 5; 3 и 6 – односторонние углы. 1 и 5; 2 и 6; 4 и 8; 3 и 7 – соответственные углы. 3 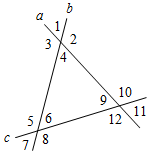 . Упражнения на закрепление знания углов, полученных при пересечении двух прямых секущей (по рис. 2). . Упражнения на закрепление знания углов, полученных при пересечении двух прямых секущей (по рис. 2).Рис. 2 – Назовите накрест лежащие углы при прямых а и b и секущей с. – Назовите односторонние углы при прямых b и с и секущей а. – Назовите соответственные углы при прямых а и с и секущей b. Д 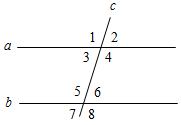 ано:4 = 5. ано:4 = 5.Рис. 3 Докажите:3 = 6; 3 = 7; 6 = 2; 4 + 6 = 180°; 5 + 2 = 180°. 4. Доказательство признаков параллельности прямых. Признак параллельности прямых, использующий накрест лежащие углы, можно доказать по учебнику | |||
| III этап. Закрепление изученного материала | ||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||
| Совершенствовать навыки решения задач на закрепление изученного материала | (Ф/И)Организует деятельность учащихся. 1. Решить задачу. Найти пары параллельных прямых (отрезков) и доказать их параллельность. 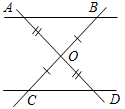 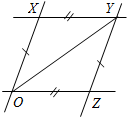 Рис. 4 Рис. 5 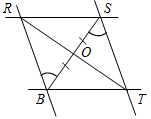 Рис. 6 2. Решить задачу № 191 на доске и в тетрадях | № 191. Дано:АВС, ВK – биссектриса, ВМ = KМ. Д 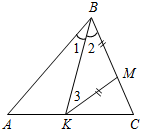 оказать:KМАВ. оказать:KМАВ.Рис. 7 Доказательство: 1) Так как ВМ = KМ, то ВМK – равнобедренный, значит, 2 = 3 (по свойству). 2) 1 = 2 (по усл.), 2 = 3 (из п. 1), 1 = 3, а так как 1 и 3 – накрест лежащие при прямых АВ и KМ и секущей ВK, то по признаку АВ KМ, что и требовалось доказать | ||
| IV этап. Итоги урока. Рефлексия | ||||
| Деятельность учителя | Деятельность учащихся | |||
| (Ф/И) – В чем заключается первый признак параллельности прямых? – Составьте синквейн к теме урока | (И) Домашнее задание: изучить пункты 24–25 (первый признак); решить задачи № 186, 188 | |||
1 ... 14 15 16 17 18 19 20 21 ... 47
Ресурсный материал
Тест
1. Выбрать рисунки с пересекающимися прямыми.
а) 1а; б) 1б; в) 1в.

а) б) в)
Рис. 1
2. Завершить высказывание, выбрав нужный пункт.
Пересекающиеся прямые имеют...
а) на чертеже одну общую точку;
б) одну общую точку.
3. Указать номера рисунков, на которых изображены параллельные прямые.
а) 2а; б) 2б; в) 2в.
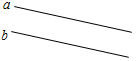
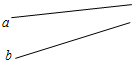
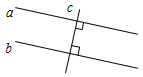
а) б) в)
Рис. 2
4. Указать неправильную концовку определения.
Две прямые на плоскости называются параллельными...
а) если они находятся на постоянном расстоянии друг от друга;
б) если они не пересекаются на плоскости;
в) если они обе перпендикулярны к третьей прямой;
г) если они не пересекаются на чертеже.
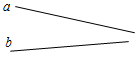
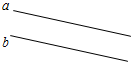
5. Указать рисунки, на которых изображены параллельные отрезки.
а) 3а; б) 3б; в) 3в; г) 3г.
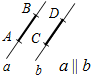
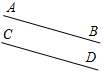
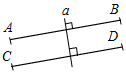
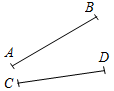
а) б) в) г)
Рис. 3
6. Указать правильную концовку определения.
Два отрезка называются параллельными, если они...
а) оба перпендикулярны третьей прямой;
б) лежат на параллельных прямых;
в) имеют одинаковое расстояние между концами;
г) не пересекаются на плоскости.
7. Указать рисунки, на которых изображены параллельные лучи.
а) 4а; б) 4б; в) 4в; г) 4г.
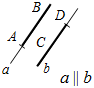
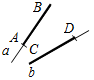
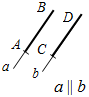
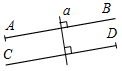
а) б) в) г)
Рис. 4
Ответы: 1 – a, б; 2 – б; 3 – в; 4 – г; 5 – а, в; 6 – б; 7 – а, в, г.
Урок30. Признаки параллельности двух прямых
| Цель деятельности учителя | Создать условия для изучения признаков параллельности двух прямых, связанных с односторонними и соответственными углами, и демонстрации их применения при решении задач | |||||
| Термины и понятия | Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы | |||||
| Планируемые результаты | ||||||
| Предметные умения | Универсальные учебные действия | |||||
| Владеют базовым понятийным аппаратом по основным разделам содержания | Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений | |||||
| Организация пространства | ||||||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |||||
| Образовательные ресурсы | • Задания для фронтальной работы. • Тест | |||||
| I этап. Активизация знаний учащихся | ||||||
| Цель деятельности | Совместная деятельность | |||||
| Систематизировать теоретические знания | (Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Повторение доказательства признака параллельности двух прямых, использующего накрест лежащие углы, по готовому чертежу на доске. 3. Устная работа по готовым чертежам на доске. Задание: Найти пары параллельных прямых (отрезков) и доказать их параллельность. 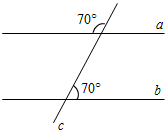 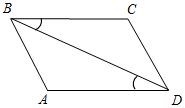 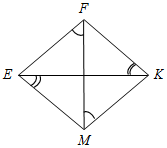 Рис. 1 Рис. 2 Рис. 3 | |||||
| II этап. Изучение новой темы | ||||||
| Цель деятельности | Совместная деятельность | |||||
| Рассмотреть признаки параллельности прямых, связанные с односторонними углами и соответственными углами | (Ф) 1.По рисунку 102 учебника, заранее начерченному на доске, учитель вместе с учащимися доказывает теорему о признаке параллельности двух прямых, связанном с односторонними углами (устно), а затем учащиеся самостоятельно должны записать доказательство теоремы в тетрадях. 2. Учащиеся самостоятельно изучают признак параллельности прямых, связанный с соответственными углами, и записывают доказательство теоремы в тетрадях. 3. Решить задачи по готовым чертежам на заготовленных плакатах (устно). Задание: Найдите пары параллельных прямых и докажите их параллельность. 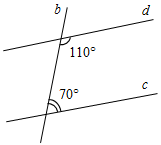 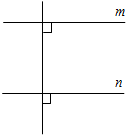 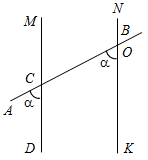 Рис. 4 Рис. 5 Рис. 6 | |||||
| III этап. Тест | ||||||
| Цель деятельности | Тестовые задания | |||||
| Проверить уровень сформированности теоретических знаний | (И)Выполнить тест с самопроверкой (см. Ресурсный материал) | |||||
| IV этап. Решение задач по готовым чертежам | ||||||
| Цель деятельности | Совместная деятельность | |||||
| На простейших задачах отработать признаки параллельности прямых | (Ф/И) Решение задач (устно). 1) Параллельны ли прямые а и b? Почему? 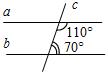 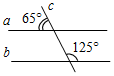 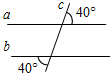 а) б) в) Рис. 7 2) Доказать: АВ || DE. 3) Доказать:АВ || MN. 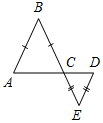 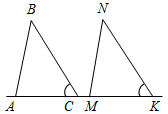 Рис. 8 Рис. 9 | |||||
| V этап. Решение задач | ||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||
| Совершенствовать навыки решения задач | (Ф/И) Организует деятельность учащихся. 1. Решить № 192 на доске и в тетрадях. 2. Познакомиться с практическими способами построения параллельных прямых (п. 26) по рисункам 103, 104, 105 учебника. 3. Выполнить задание № 195 | № 192. Дано:АВС, А = 40°, ВСЕ, АСВ – смежные, ВСЕ = 80°, CK – биссектриса ВСЕ. Доказать:АВ || CK. Р 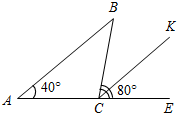 ис. 10 ис. 10Д 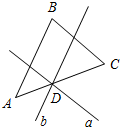 оказательство: оказательство:1) Так как CK – биссектриса ВСЕ, то ВCK = KCЕ = 40°. 2) ВАС и KCЕ – соответственные при прямых АВ, CK и секущей АС, ВАС = KCЕ = 40°, АВ || CK, что и требовалось доказать. № 195. а || ВС, b || АВ Рис. 11 | ||||
| VI этап. Итоги урока. Рефлексия | ||||||
| Деятельность учителя | Деятельность учащихся | |||||
| (Ф/И) – Перечислите признаки параллельности прямых. – Оцените свою работу на уроке. – Задайте три вопроса по теме урока | (И) Домашнее задание: изучить пункты 24–26; ответить на вопросы 1–6 на с. 66; решить задачи № 193, 194 | |||||
1 ... 15 16 17 18 19 20 21 22 ... 47
Ресурсный материал
Тест
1
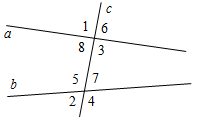 . Выберите верные утверждения (по рис. 1):
. Выберите верные утверждения (по рис. 1): а) 1 и 3 – вертикальные; д) 2 и 4 – смежные;
б) 5 и 1 – односторонние; е) 7 и 1 – накрест лежащие;
в) 7 и 6 – соответственные; ж) 3 и 7 – односторонние.
г) 5 и 3 – накрест лежащие;
Рис. 1
2. Выберите верные утверждения (по рис.1).
Прямые а и b параллельны, если…
a) l = 3; д) 5 = 3;
б) 8 + 5 = 180°; e) 2 = 6;
в) 7 = 6; ж) 1 + 4 = 180°;
г) 8 + 3 = 180°; и) 1 + 7 = 180°.
3. Укажите продолжения высказывания, не соответствующие действительности.
Прямые не параллельны, если при пересечении двух прямых секущей…
а) сумма односторонних углов не равна 180°;
б) сумма соответственных углов равна 180°;
в) вертикальные углы не равны;
г) накрест лежащие углы не равны;
д) сумма смежных углов не равна 180°;
е) соответственные углы не равны.
Ответы: 1 – а, в, г, д, ж; 2 – б, в, д, е, и; 3 – а, г, е.
Урок 31. Решение задач
на применение признаков параллельности прямых
| Цели деятельности учителя | Создать условия для закрепления и систематизации изученного материала, обучения применению признаков параллельности прямых при решении задач; способствовать развитию логического мышления учащихся; содействовать воспитанию аккуратности при построении чертежей на доске и в тетрадях | |||
| Термины и понятия | Параллельные прямые, накрест лежащие углы, соответственные углы, односторонние углы | |||
| Планируемые результаты | ||||
| Предметные умения | Универсальные учебные действия | |||
| Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, имеют достаточно высокий уровень пространственных представлений и изобразительных умений, владеют навыками геометрических построений | Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать самостоятельно. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений | |||
| Организация пространства | ||||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |||
| Образовательные ресурсы | • Чертежи к задачам. • Задания для самостоятельной работы | |||
| I этап. Актуализация опорных знаний учащихся | ||||
| Цель деятельности | Совместная деятельность | |||
| Систематизировать теоретические знания | (Ф/И) 1. Проверить правильность выполнения домашнего задания. 2. Провести теоретический опрос по признакам параллельности прямых. 3. Решить задачи по готовым чертежам (устно). 1) Докажите, что а || b. 2) Докажите, что а || с. 3)Докажите, что а || b и т || п, если 1 = 2 = 3. 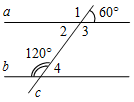 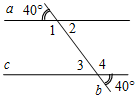 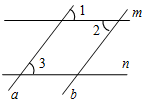 Рис. 1 Рис. 2 Рис. 3 4) Дано:1 = 83°, 2 больше 1 на 14°.5) Дано:2 = 114°, 1 меньше 2 на 20°. Параллельны ли прямые MN и AB?Параллельны ли прямые СЕ и AB? 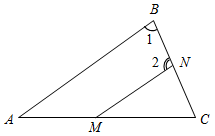 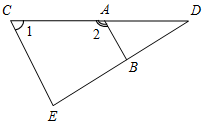 Рис. 4 Рис. 5 | |||
| II этап. Решение задач | ||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||
| Совершенствовать навыки решения задач | (Ф/И) Организует деятельность учащихся. 1. Решить задачу № 190 по рисунку 109 (на доске и в тетрадях). 2. Решить задачу № 213 по рисунку 121 (на доске и в тетрадях). 3. Решить задачу № 215 по рисунку 122 (устно). Указание: рисунок 122 заранее перенести на доску и ввести цифровые обозначения углов. Сначала доказывается параллельность прямых а и b (сумма односторонних углов: 115° + 65° = = 180°) | № 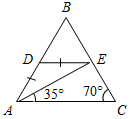 190. 190.Дано:АВ = ВС, АD = DЕ, С = 70°, ЕАС = 35°. Доказать:DЕ || АС. Рис. 6 Доказательство: 1) Так как АВ = ВС, то А = С = 70° (свойство равнобедренного треугольника). 2) Так как ЕАС = 35°, А = 70°, то DАЕ = 35°. 3) Так как АDЕ – равнобедренный, то DАЕ = DЕА = 35° (по свойству). 4) DЕА = ЕАС = 35°. DЕА и ЕАС – накрест лежащие при прямых DЕ и АС и секущей АЕ. DЕ || АС, что и требовалось доказать. № 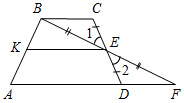 213. 213.Дано: СЕ = ЕD, ВЕ = EF, KE || AD. Доказать: KE || BC. Рис. 7 Доказательство: 1) Рассмотрим ВСF и FDЕ. ВЕ = EF (по усл.), СЕ = ЕD (по усл.), 1 = 2 (вертик.), тогда ВСЕ = FDЕ (по двум сторонам и углу между ними), СВЕ = DFЕ (по определению равных треугольников). 2) СВЕ = DFЕ – накрест лежащие при прямых BC и AD и секущей ВF, СВЕ = DFЕ (по п. 1), тогда BC || AD по признаку. 3) KE || AD (по усл.), BC || AD (из п. 2), тогда KE || BC (свойство параллельных прямых), что и требовалось доказать | ||
| III этап. Самостоятельная работа | ||||
| Цель деятельности | Задания для самостоятельной работы | |||
| Проверить умение применять признаки параллельности при решении задач | (И) Самостоятельная работа выполнятеся на листках и сдается на проверку учителю (см. Ресурсный материал) | |||
| IV этап. Итоги урока. Рефлексия | ||||
| Деятельность учителя | Деятельность учащихся | |||
| (Ф/И) – Оцените свою работу на уроке. – Задайте три вопроса по теме | (И) Домашнее задание: повторить материал пунктов 24–26; решить задачи № 214, 216 | |||
1 ... 16 17 18 19 20 21 22 23 ... 47