Файл: Урок Прямая и отрезок.docx

Ресурсный материал

Самостоятельная работа

Вариант I

1. Параллельны ли прямые d и е, изображенные на рисунке 1?

2. На рисунке 2 точка О – середина отрезков EL и KF. Докажите, что EF || KL.

Вариант II

1. Параллельны ли прямые m и n, изображенные на рисунке 3?

2. На рисунке 4 точка F – середина отрезков MО и NP. Докажите, что MN || PO.

Вариант III

1. Какие из прямых, изображенных на рисунке 5(m, n и p), являются параллельными? Ответ обоснуйте.

2. В равнобедренных треугольниках СDЕ и FPK, изображенных на рисунке 6, 1 = 2. Докажите, что СD || PF.

Вариант IV

1. На рисунке 7 МD = NP, 1 = 2. Докажите, что MN || DP.

2. В равнобедренных треугольниках АВС и DЕF, изображенных на рисунке 8, 1 = 2. Докажите, что AB || EF.



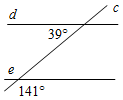
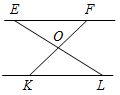
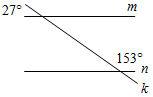
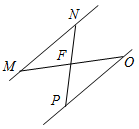
Рис. 1 Рис. 2 Рис. 3 Рис. 4



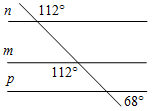
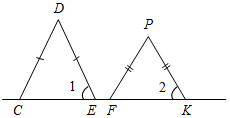
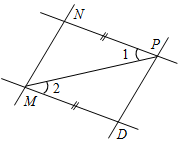
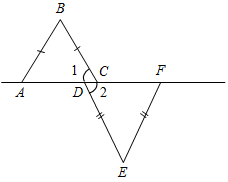
Рис. 5 Рис. 6 Рис. 7 Рис. 8

Урок 32. Об аксиомах геометрии.
Аксиома параллельности прямых

Цель деятельности учителя	Создать условия для формирования представления об аксиомах геометрии, введения аксиомы параллельных прямых и следствия из нее
Термины и понятия	Параллельные прямые, аксиома
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, имеют пространственные представления и достаточно высокий уровень развития изобразительных умений, навыков геометрических построений		Познавательные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для фронтальной работы. • Историческая справка об аксиоме параллельных прямых
I этап. Актуализация опорных знаний
Цель деятельности	Совместная деятельность
Проанализировать ошибки, допущенные в самостоятельной работе	(Ф/И) 1. Сообщить результаты самостоятельной работы. 2. Проверить правильность выполнения домашнего задания
II этап. Беседа по новой теме
Цель деятельности	Совместная деятельность
Ввести понятие аксиомы, рассмотреть аксиому параллельных прямых	(Ф/И) 1. Беседа об аксиомах геометрии (см. пункт 27 и приложение 1 учебника). 2. Самостоятельное решение задачи с последующим обсуждением. Задание: Через точку А, не лежащую на прямой а, провести прямую, параллельную прямой а. Х 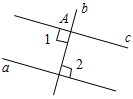од построения(рис. 1): 1) провести через точку А прямую b так, что ab; 2) провести через точку А прямую с так, что bс. Рис. 1 Доказательство:1 = 2 = 90°, то есть накрест лежащие углы при прямых а и с и секущей b равны, следовательно, а || с. Вопросыучащимся: 1) Всегда ли через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной? 2) Сколько прямых, параллельных данной, можно провести через точку, не лежащую на данной прямой? 3) Можно ли доказать, что через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной? – Математики с древних времен пытались доказать данное утверждение. В «Началах» Евклида оно называется пятым постулатом. Попытки доказать пятый постулат Евклида не увенчались успехом, и лишь в XIX веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой. Огромную роль в решении этого вопроса сыграл русский математик Николай Иванович Лобачевский. Итак, аксиомапараллельных прямыхгласит: «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной». – Является ли утверждение «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной» аксиомой? Почему? (Это утверждение не является аксиомой, так как оно доказывается.) – Чем отличаются вышеуказанные утверждения? (Аксиома параллельных прямых говорит о единственности такой прямой, а другое утверждение – о существовании такой прямой.)
III этап. Закрепление изученного материала
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения простейших задач	(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 196, 197 (устно). Указание: при решении задачи № 197 полезно показать учащимся на рисунке два возможных случая расположения прямых: 1) все четыре прямые пересекают прямую р; 2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее. Эти два случая иллюстрируют ответ на вопрос задачи: по крайней мере, три прямые пересекают прямую р. 2. Разъяснить смысл понятия «следствия». Записать в тетрадях: «Следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем». 3. Рассмотреть следствия 1 и 2 из аксиомы параллельных прямых. 4. Решить задачи № 198, 200, 218. 5. Решить задачу № 219		№ 218. Д 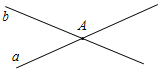ано:аb = А. Можно ли построить прямую с, такую, что: 1) а || с; 2) сb? Рис. 2 Доказательство: Возьмем любую точку Ма. По аксиоме параллельных прямых, через точку М можно построить прямую с, параллельную а, и притом только одну. Так как а || с, аb, тогда сb. Значит, можно построить такую прямую, параллельную прямой а и пересекающую прямую b. № 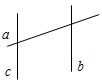219. Дано:с а, сb, с – любая. Доказать: а || b. Рис. 3 Доказательство: Пусть а || b. Проведем прямую с || b; с а, но сb (по построению), а это противоречит условию. Следовательно, а || b, что и требовалось доказать
IV этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Что нового узнали на уроке? – В чем заключается аксиома Евклида? – Составьте синквейн к уроку			(И) Домашнее задание: изучить пункты 27 и 28; ответить на вопросы 7–11 на с. 66–67 учебника; решить задачи № 217, 199

---

Урок33. Свойства параллельных прямых

Цель деятельности учителя		Создать условия для рассмотрения свойств параллельных прямых, демонстрации применения свойств параллельных прямых, закрепления знаний, умений, навыков учащихся по теме «Аксиома параллельных прямых»
Термины и понятия		Параллельные прямые, аксиома, свойства параллельных прямых
Планируемые результаты
Предметные умения			Универсальные учебные действия
Владеют геометрическим языком, умеют его использовать для описания предметов окружающего мира, владеют достаточно высоким уровнем развития пространственных представлений и изобразительных умений, навыков геометрических построений			Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве; подбирают аргументы для доказательства своей позиции, формулируют выводы. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
Организация пространства
Формы работы		Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы		• Тест. • Таблица
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать теоретический материал	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Тест с последующей самопроверкой (см. Ресурсный материал). (Задания 1 и 2 выполняются одновременно; 3 ученика работают у доски, остальные в тетрадях.)
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Ввести свойства параллельных прямых	(Ф/И) 1. Решение задач. 1) Доказать:АВ || CD. 2) Дано: АВ || CD. Найти:EKC. 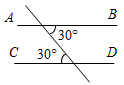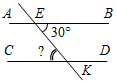Рис. 1 Рис. 2 Следует обратить внимание учащихся, что в первой задаче а || bпо первому признаку параллельности прямых, а вторая задача является обратной первой, и в этом случае мы не знаем, равны ли накрест лежащие углы, если прямые параллельны. Таким образом, перед учащимися поставлена проблема, которую необходимо разрешить. Условие. Пусть а || b, с – их секущая, 1 и  2 – накрест лежащие углы, образованные данными прямыми. Требуется выяснить, равны ли 1 и  2. Решение этой задачи можно построить так же, как доказательство свойства накрест лежащих углов при параллельных прямых и их секущей по учебнику. Вывод. Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны. – Это утверждение называют свойством накрест лежащих углов при параллельных прямых и их секущей. 2. Информация для учащихся. – Во всякой теореме различают две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – то, что требуется доказать. Вывод. Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы. 3. Беседа о методе доказательства от противного по учебнику. 4. Доказательства следствия свойства накрест лежащих углов при параллельных прямых и их секущей и свойств соответственных и односторонних углов при параллельных прямых и их секущей. Можно предложить учащимся провести доказательства самостоятельно в ходе выполнения упражнений. – Докажите, что если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и другой. – Сформулируйте теорему, обратную признаку параллельности прямых, использующему соответственные углы. Дайте название полученной теореме и докажите ее. – Сформулируйте теорему, обратную признаку параллельности прямых, использующему односторонние углы. Дайте название полученной теореме и докажите ее. – Заполните таблицу. Название теоремы Признак параллельности прямых Свойство параллельности прямых Формулировка теоремы Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны Условие (дано) Прямые а, b; с – их секущая; 1, 2 – накрест лежащие углы; 1 = 2 Прямые а, b; с – их секущая; 1, 2 – накрест лежащие углы; а || b Заключение (доказать) а || b 1 = 2 – В чем заключается разница между этими теоремами?

1   ...   17   18   19   20   21   22   23   24   ...   47

---

III этап. Решение задач

Цель деятельности

Совместная деятельность

На простейших задачах отработать умение применять свойства параллельных прямых

(Ф/И)

Устно решить № 201, 205 по рисунку 117 и № 209 по рисунку 118

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

– Перечислите свойства параллельных прямых.

– Что такое доказательство методом от противного?

– Оцените свою деятельность на уроке

(И) Домашнее задание: изучить п. 29; повторить пункты 15–28; ответить
на вопросы 1–15 на с. 66–67 учебника; решить задачи № 202, 212


Ресурсный материал

Тест

1. Вычеркнуть лишние слова в скобках.

Аксиома – это (очевидное, принятое, исходное) положение геометрии, не требующее (объяснений, доказательств, обоснований).

2. Выбрать окончание формулировки аксиомы параллельных прямых.

Через точку, не лежащую на данной прямой…

а) проходит только одна прямая, параллельная данной;

б) всегда проходит прямая, параллельная данной;

в) проходит только одна прямая, не пересекающаяся с данной.

3. Что может быть следствием аксиомы или теоремы? Указать неверные ответы.

а) Утверждение, не требующее доказательства.

б) Новая теорема, для доказательства которой использована аксиома или теорема.

в) Утверждение, непосредственно выводимое из аксиомы или теоремы.

4. Указать следствия аксиомы параллельных прямых.

а) Если отрезок или луч пересекает одну из параллельных прямых, то он пересекает и другую.

б) Если две прямые параллельны третьей прямой, то они параллельны друг другу.

в) Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

г) Если три прямые параллельны, то любые две из них параллельны друг другу.

д) Если две прямые не параллельны третьей прямой, то они не параллельны между собой.

е) Если прямая пересекает одну из параллельных прямых, то она не может не пересекать другую.

ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.

5. Указать правильный ответ на вопрос.

Если через точку, лежащую вне прямой, проведено несколько прямых, то сколько из них пересекаются с исходной прямой?

---

а) Неизвестно, так как не сказано, сколько прямых проведено через точку.

б) Все, кроме параллельной прямой.

в) Все, которые имеют на рисунке точку пересечения с исходной прямой.

6. Почему если одна из прямых, проходящих через точку, лежащую вне заданной прямой, параллельна этой прямой, то другие прямые, проходящие через эту точку, не могут быть ей параллельны? Указать неправильный ответ на этот вопрос.

а) Это противоречит аксиоме параллельных прямых.

б) Любая другая прямая, если она также параллельна заданной, совпадет с первой.

в) Все другие прямые имеют точку пересечения с заданной прямой, хотя она может находиться на сколь угодно большом расстоянии от исходной точки.

Ответы: 1. Следует вычеркнуть слова: «очевидно», «принятые», «объяснений», «обоснований»; 2 – а; 3 – а, б; 4 – б, в, е, ж; 5 – б; 6 – в.

Урок34. Свойства параллельных прямых.
Решение задач

Цели деятельности учителя	Создать условия для закрепления знания свойств параллельных прямых в ходе выполнения упражнений и решения задач, для систематизации знаний учащихся; способствовать развитию логического мышления учащихся
Термины и понятия	Параллельные прямые, аксиома, свойства параллельных прямых
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию		Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве; подбирают аргументы для доказательства своей позиции, формулируют выводы. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); парная (П)
Образовательные ресурсы	• Задания для индивидуальной работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Выявить уровень сформированности теоретических знаний	(Ф/И) 1. Проверка домашнего задания. (И) 2. Проверочная работа на 10 минут. Работа выполняется на листочках и сдается на проверку учителю. Вариант I 1. Сформулируйте аксиому параллельных прямых. 2. Какая теорема называется обратной данной теореме? Приведите примеры теорем, обратных данным. 3. Докажите, что при пересечении двух параллельных прямых секущей соответственные углы равны. ВариантII 1. Объясните, какие утверждения называются аксиомами. Приведите примеры аксиом. 2. Дайте определение параллельных прямых. Какие два отрезка называются параллельными? 3. Докажите, что при пересечении двух параллельных прямых секущей сумма односторонних углов равна 180°
II этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения задач по данной теме	(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 203 на доске и в тетрадях. (П) 2. Решить № 205. (Ф/И) 3. Решить № 220 по готовому чертежу (устно)		№ 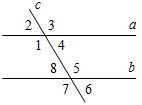203. Дано:а || b, с – секущая. а) 1 = 150°; б) 1 >4 на 70°. Найти: величину углов. Рис. 1 Решение: а) 1) Если 1 = 150° (по усл.), то 3 = 1 = 150° (как вертикальные); 5 = 1 = 150° (как накрест лежащие при а || b и секущей с); 7 = 5 = 150° (как вертикальные). 2) 1, 4 – смежные, значит, 1 + 4 = 180° (по свойству), 4 = 180° – 150° = 30°; 2 = 4 = 30° (как вертикальные), 8 = 4 = 30° (как накрест лежащие при а || b и секущей с); 6 = 8 = 30° (как вертикальные). Ответ: 30°, 150°, 30°, 150°, 30°, 150°, 30°. б) Если 1 >4 на 70°, то примем 1 = х, следовательно, 4 = х – 70°; так как 1, 4 – смежные, то х + (х – 70) = 180 2х = 250 х = 125 1 = 125°, 4 = 55° Рассуждая аналогично пункту (а), имеем: 1 = 3 = 5 = 7 = 125°, 2 = 4 = 6 = 8 = 55°. О 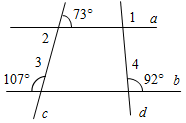твет: 125°, 55°. № 205. Найти:1. Рис. 2 Доказательство: 1) 2 – вертикальный с углом 73°, значит 2 = 73°. 2) 2, 3 – односторонние при прямых а, b и секущей с. 2 + 3 = 73° + 107° = 180°, тогда, а || b (по признаку). 3) 1, 4 – соответственные углы при прямых а || b и секущей d, значит, 1 = 4 = 92° (по свойству параллельных прямых). Ответ: 92°
III этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Перечислите свойства параллельных прямых. – Перечислите признаки параллельных прямых. – Оцените свою работу на уроке и работу своего товарища			(И)Домашнее задание: повторить изученный материал пунктов 24–29; ответить на вопросы 1–15 на с. 66–67 учебника; подготовиться к устному опросу; решить задачи № 206, 208, 211

---

Урок35. Решение задач

Цель деятельности учителя	Создать условия для приведения в систему знаний учащихся по данной теме, четкого понимания учащимися того, когда в задаче нужно применить признак параллельности двух прямых, а когда – свойство параллельных прямых
Термины и понятия	Параллельные прямые, аксиома, свойства параллельных прямых
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию		Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Карточки для устного опроса. • Чертежи к задачам

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать теоретические знания учащихся	(Ф/И) 1. Обсуждение результатов проверочной работы и анализ допущенных ошибок. 2. Проверка правильности выполнения домашней работы. Для этого к доске вызываются трое учащихся и демонстрируют решения домашних задач. 3. Устный опрос учащихся по карточкам (см. Ресурсный материал)
II этап. Решение задач по готовым чертежам
Цель деятельности	Совместная деятельность
Совершенствовать навыки решения простейших задач	(И) 1. Решить задачи по готовым чертежам, сделав в тетрадях краткие записи (см. Ресурсный материал) (самостоятельно). (Ф/И) 2. Решить задачу (один ученик решает у доски, остальные в тетрадях). Дано:АВ || DE(рис. 1а). Доказать:1 + 2 = 3. 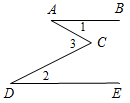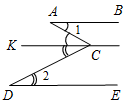а) Рис. 1 б) Подсказка: через точку С проведите прямую, параллельную АВ. Доказательство(см. рис. 1б): 1) Через точку С, не лежащую на прямой АВ, можно провести прямую, параллельную АВ, и притом только одну. 2) Так как KС || АВ, а АВ || DE по условию задачи, то KС || DE. 3) 1 = ACK, как накрест лежащие при параллельных прямых АВ и KС и секущей АС. 4) 2 = KСD, как накрест лежащие при параллельных прямых KС и DE и секущей DС. Так как 1 = АСK, 2 = KСD, a 3 = АСK + KСD, то 3 = 1 + 2, что и требовалось доказать
III этап. Самостоятельное решение задач
Цель деятельности	Задания для самостоятельной работы
Совершенствовать навыки решения задач	(И) Учащимся предложены задачи двух уровней сложности (см. Ресурсный материал). Они сами выбирают, задачи какого уровня будут решать. В конце урока тетради можно собрать на проверку
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Что повторили на уроке? – Оцените свою работу на уроке		(И)Домашнее задание: решить № 207

---