Файл: Задача Методом изоклин построить интегральные кривые уравнения. Решение.docx
Добавлен: 22.11.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
Математика
Группа 22Э211в
Студент
Новицкая А.А
МОСКВА 2023
Задача 1. Методом изоклин построить интегральные кривые уравнения
1.1.
.Решение:
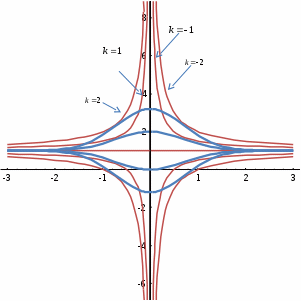
Задавая различные значения параметра k, можно получить семейство кривых, каждая из которых является изоклиной при определённом значении параметра k. Построение изоклин один из приёмов качественного анализа поведения решений анализируемого дифференциального уравнения.У нас
Это уравнения изоклин.
При
получаем уравнение прямой 
, при 
получаем семейство гипербол с центром в точке (0;1). При 
, при 
.Построим график (изоклины (гиперболы для
и 
и прямая для k = 0) – красным цветом, интегральные кривые – синим):
Задача 2. Решить уравнение, допускающее понижение порядка
2.1.
.
Решение:
Это дифференциальное уравнение 2-го порядка. Оно позволяет снизить его порядок путем подстановки
, потому что не содержит функцию у. Вторая производная:
. Тогда после подстановки 
, где 
. Это уравнение с разделяющимися переменными.
Разделяем переменные:
.Пронтегрируем обе части этого равенства:
.Возвращаемся к переменной у:
получаем:
, 
, 
.Переменные разделены. Интегрируем обе части равенства:
.
- общее решение.Ответ:
.Задача 3. Решить систему уравнений
3.1.
Решение: присвоим уравнениям системы номера (1) и (2).
Сначала из уравнения (1) выражаем переменную
. Подставляем это выражение в уравнение (2), получаем: 
Это уравнение с разделяющимися переменными.
Разделяем переменные:
Интегрируем обе части:
,
.Подставляем полученное выражение в уравнение (1):
. Разделяем переменные и интегрируем обе части:
,
, 
.Тогда для функции
: 
. Ответ: Общее решение системы имеет вид
.Задача 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?
Решение: данная задача принадлежит к схеме испытаний Бернулли:
Пусть проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью p и не происходит с вероятностью q = 1 – p.
Наивероятнейшее число появлений события в схеме Бернулли находится из двойного неравенства:
.У нас
. Нужно найти число испытаний n, при котором наивероятнейшее число появлений события 
= 10.Подставляем наши данные:
целое число, удовлетворяющее этому неравенству, равно 
.Ответ:
.