Добавлен: 22.11.2023
Просмотров: 262
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
участок 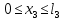 , идем слева:
, идем слева: 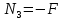 .
.
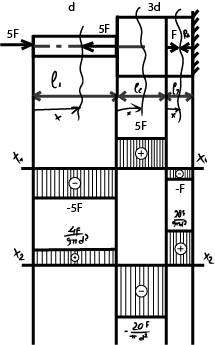
Построение эпюров нормальных напряжений:
 участок
участок  :
:
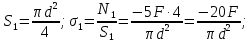
 участок
участок  :
:
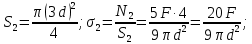
 участок
участок 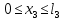 :
:
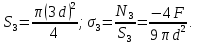
Опасным сечением является любое сечение участка 1:
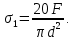
Определение диаметра d из условия прочности при растяжении/сжатии:
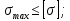
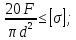
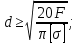
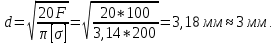
Определение деформации – общего удлинения (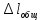 :
:
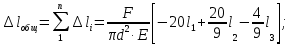
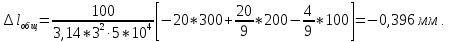
Вывод: Диаметр d=3 мм. Общее удлинение равняется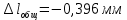 , то есть брус сжимается.
, то есть брус сжимается.







Из условия равновесия определяются реакции шарниров. Записываются уравнения равновесия:
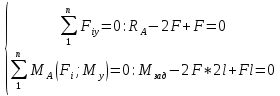
Отсюда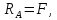
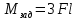 .
.
Далее балка разбивается на два участка.
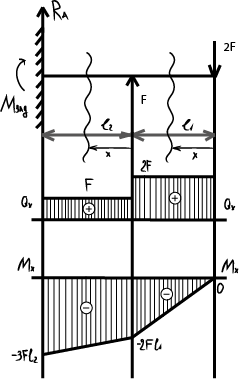
Построение эпюр поперечных сил:
 участок,
участок,  , идем справа:
, идем справа:
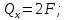
 участок,
участок,  , идем справа:
, идем справа:
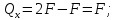
Построение эпюр изгибающих моментов:
 участок,
участок,  , идем справа:
, идем справа:
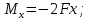
При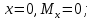
При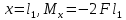 .
.
 участок,
участок,  , идем справа:
, идем справа:
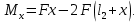
При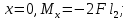
При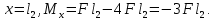
Опасным сечением является: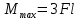 .
.
Определение размеров поперечного сечения балки из условия прочности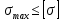 .
.
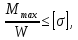
где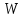 – момент сопротивления площади поперечного сечения
– момент сопротивления площади поперечного сечения
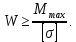
Для поперечного круглого сечения балки:
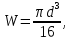
где d – диаметр сечения.
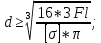
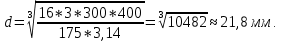
Отсюда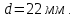
Найдем величину прогиба при поперечном изгибе, для этого составим уравнение изгибающихся моментов. Для этого помещаем балку в систему координат. В результате балка имеет два участка:
 уч.
уч. 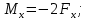
 уч.
уч. 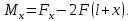
Дифференциальное уравнение упругой линии балки:
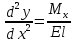
где ???? – момент инерции площади поперечного сечения балки;
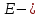 модуль продольной упругости.
модуль продольной упругости.
Для круглого сечения:
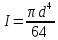
 участок:
участок:
Первое интегрирование: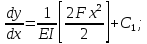
Второе интегрирование: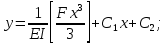
 участок:
участок:
Первое интегрирование: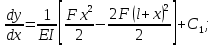
Второе интегрирование: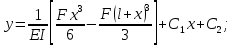
Получаем систему:
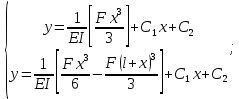
Определяя постоянных интегрирования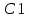 и
и 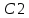 воспользуемся граничными условиями. Если х=0, то у=0 выполняется на первом участке, если x=2l, то у=0 выполняется на втором участке.
воспользуемся граничными условиями. Если х=0, то у=0 выполняется на первом участке, если x=2l, то у=0 выполняется на втором участке.
Получаем уравнения:
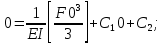 получаем
получаем 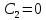 .
.
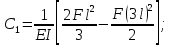
Тогда:
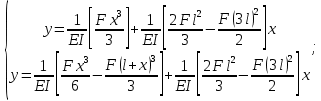
Рассчитываем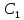 :
:
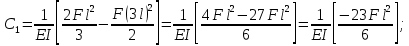
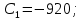
Вывод: Диаметр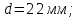 постоянные интегрирования
постоянные интегрирования
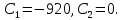
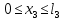 , идем слева:
, идем слева: 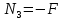 .
.
Построение эпюров нормальных напряжений:
 участок
участок  :
: 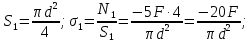
 участок
участок  :
: 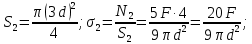
 участок
участок 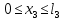 :
: 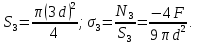
Опасным сечением является любое сечение участка 1:
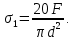
Определение диаметра d из условия прочности при растяжении/сжатии:
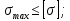
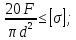
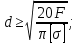
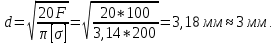
Определение деформации – общего удлинения (
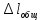 :
: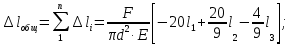
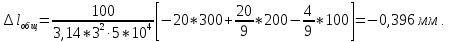
Вывод: Диаметр d=3 мм. Общее удлинение равняется
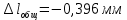 , то есть брус сжимается.
, то есть брус сжимается.3.2 Построение эпюра поперечных сил и изгибающих моментов.







Из условия равновесия определяются реакции шарниров. Записываются уравнения равновесия:
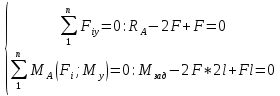
Отсюда
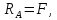
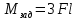 .
.Далее балка разбивается на два участка.

Построение эпюр поперечных сил:
 участок,
участок,  , идем справа:
, идем справа: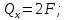
 участок,
участок,  , идем справа:
, идем справа: 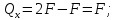
Построение эпюр изгибающих моментов:
 участок,
участок,  , идем справа:
, идем справа: 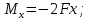
При
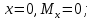
При
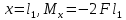 .
. участок,
участок,  , идем справа:
, идем справа: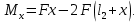
При
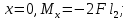
При
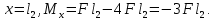
Опасным сечением является:
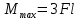 .
.Определение размеров поперечного сечения балки из условия прочности
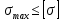 .
.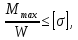
где
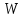 – момент сопротивления площади поперечного сечения
– момент сопротивления площади поперечного сечения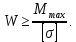
Для поперечного круглого сечения балки:
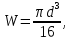
где d – диаметр сечения.
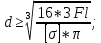
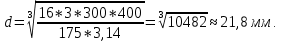
Отсюда
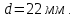
Найдем величину прогиба при поперечном изгибе, для этого составим уравнение изгибающихся моментов. Для этого помещаем балку в систему координат. В результате балка имеет два участка:
 уч.
уч. 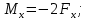
 уч.
уч. 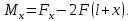
Дифференциальное уравнение упругой линии балки:
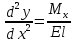
где ???? – момент инерции площади поперечного сечения балки;
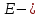 модуль продольной упругости.
модуль продольной упругости.Для круглого сечения:
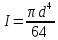
 участок:
участок:Первое интегрирование:
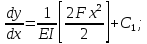
Второе интегрирование:
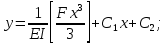
 участок:
участок: Первое интегрирование:
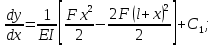
Второе интегрирование:
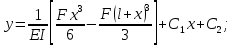
Получаем систему:
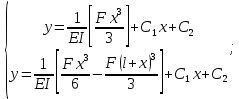
Определяя постоянных интегрирования
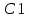 и
и 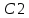 воспользуемся граничными условиями. Если х=0, то у=0 выполняется на первом участке, если x=2l, то у=0 выполняется на втором участке.
воспользуемся граничными условиями. Если х=0, то у=0 выполняется на первом участке, если x=2l, то у=0 выполняется на втором участке.Получаем уравнения:
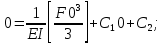 получаем
получаем 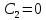 .
.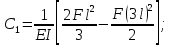
Тогда:
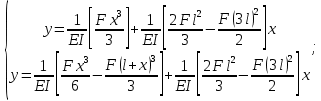
Рассчитываем
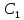 :
: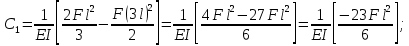
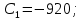
Вывод: Диаметр
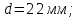 постоянные интегрирования
постоянные интегрирования 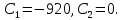
4. Список литературы
-
Чуракова Л.Д. Прикладная механика: Методические указания к курсовой работе по теме: Синтез, кинематический анализ механизма, расчет на прочность /СПбГУТ.-СПб., 2012.