Файл: 2. 3 Математическая модель объекта управления 1 Математическая модель основного контура управления.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.3 Математическая модель объекта управления
2.3.1 Математическая модель основного контура управления
Выявим факторы, влияющие на температуру жидкости. Для этого составим уравнение теплого баланса
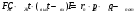,где
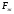- расход жидкости на входе теплообменика кг/с; 
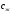- улельная теплоемкость жидкости 
, 
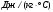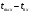- температура жидкости на выходе и входе в теплообменик, 
; 
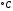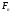- расход греющего пара, кг/с; 
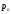- давление греющего пара в заводской магистрали, Па; 
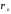- удельная теплота конденсации, 
; 
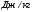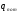- тепловые потери, Вт.Запишем уравнение материального баланса для межтрубного пространства теплообменика:
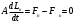,где A – площадь свободного сечения межтрубного пространства, заполненая конденсатом,
; 
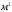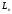- уровень конденсата в межтрубном пространстве, м; 
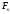-расход конденсата, кг/с.Уравнение теплопередачи через стенку трубы теплообменика:
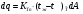,где q – тепловой поток через стенку трубы,
;
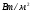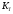- коэффициент теплопередачи, 
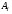- поверхность трубы теплообменика, 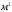.Из уравнения (2.1) выразим температуру жидкости на выходе из теплообменика:
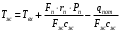
В результате линеаризации в окрестности заданного режима получим :
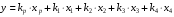
где
;
;
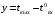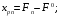
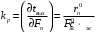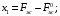
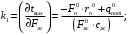
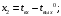
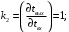
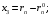
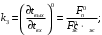
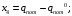
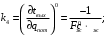
Здесь индекс р означает «по каналу регулирования».
Для определения динамических характеристик по каналу регулирования «расход пара – температура жидкости на выходе теплообменика», составим структурную схему рис.1
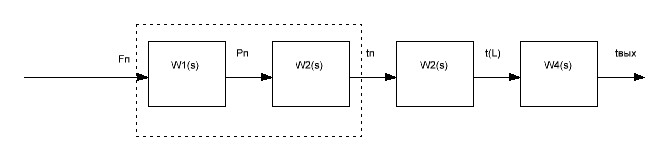
Вначале разберем динамику первого , второго и четвертого звеньев. Динамика первого звена соответствует изменению давления пара в межтрубном пространстве при изменении расхода пара и может быть представлена дифферинциальным уравнением первого порядка, имеющий после процедуры линеаризации следующий вид:
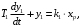
где
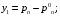
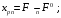
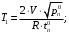
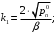
Здесь V – объём межтрубного пространства,
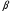- безразмерный расходный коэффициент регулирующего клапана на линии конденсата; R – газовая постоянная.Второе звено представим как статическое звено нулевого порялдка(усилительное), в котором находит свое отражение зависимость
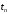от его давления 
. 
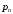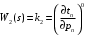
можно найти по диаграмме состояния пара при
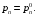
Итоговая передаточная функция межтрубного пространства выглядит следующим образом:
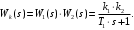
Четвертое звено учитывающее инерционность выходной камеры для нагретой жидкости, аппроксимируется статическим звеном первого порядка:
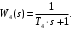
Теперь рассмотрим третье звено. Это звено показывает взаимосвязь между температурой пара в межтрубном пространстве
и температурой жидкости на выходе из труб 
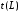.Принимаем следующие допущения:
-температура жидкости распределена по длине труб, в поперечном же сечении градиент труб отсутствует.
-теплопроводность стенки трубы такова, что стенка трубы рассматривается как звено с сосредоточеными координатами.
-тепловой емкостью пленки конденсата и тепловыми потерями можно пренебречь; теплофизические параметры жидкости и стенки трубы постоянны.
Запишем уравнение теплового баланса для потока жидкости на элементарном участке трубы
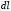в виде: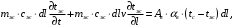
или
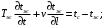
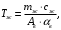
где
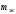- масса жидкости , заполняющая участок трубы длиной 1м,кг/м; 
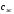- удельная теплоемкость жидкости, 
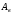- площадь внутренней поверхности теплообмена; 
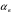- коэффициент теплоотдачи на наружной поверхности трубы.Уравнение теплового баланса для стенки трубы:
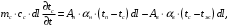
или
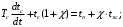
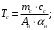
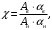
где
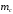
- масса трубы отнесенная к 1 метру ее длины, кг/м;
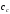- удельная теплоемкость стенки трубы; 
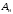- площадь наружной поверхности теплообмена; 
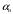- коэффициент теплоотдачи на наружной поверхности трубы.В уравнениях (2.4), (2.5) переходим к отклонениям переменных от их номинальных значений и обознчаем :
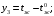
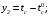
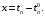
Чтобы получить передаточную функцию звена из дифферинциальных уравнений в частных производных, применяем преобразования Лапласа по t, обозначая изображения входных и выходных координат
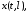
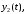
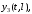
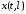через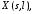 
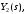
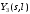соответсвенно.После преобразования по Лапласу уравнения имеют вид:
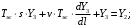
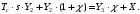
Если исключить из уравнений
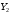, получим обыкновенное диффиринциальное уравнение первого порядка с коэффициентами, являющимися функциями комплексной перменной: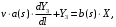
где
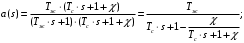
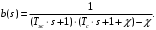
Решение уравнения при граничном условии
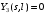для 
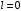и при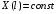 
имеет вид: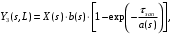
где
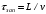- время транспортного запаздывания.Из (2.11) находим передаточную функцию третьего звена:
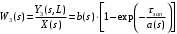
Выражение
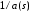аппроксимируется линейным двухчленом:
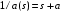.С учетом (2.13) изменим показатель экспоненты:
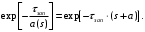
Окончательно передаточная функция третьего звена выглядит как :
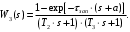
Таким образом передаточная функция третьего звена выглядит как:
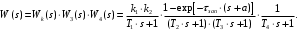
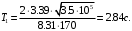
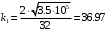
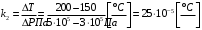,чтобы перейти к безразмерным единицам поделим на градус цельсия и умножим на 1 бар:
.
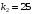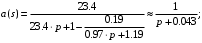
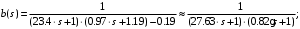
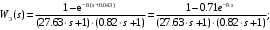
Для четвертого звена постоянная времени будет равна:
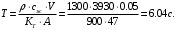
Передаточная функция четвертого звена :
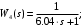
Итоговая передаточная функция :
;
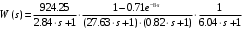