ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 6. Конечно-элементная сетка при продольном сдвиге грунта
Введем необходимые обозначения: h— размер конечного элемента;
i,i−1,i+1,...— номера узлов конечно-элементной сетки; j,j−1,j+
+ 1, . . .— номера конечных элементов; qi, qi−1, qi+1, . . . — продольные силы, действующие на конечные элементы длиной h (значения погон-
ной силы).
Запишем функцию Лагранжа двухэлементной системы как
L= Э− A, (9)
где Э— энергия деформации этой системы; A— работа сил, прило- женных к этой системе.
Условие минимума функции Лагранжа имеет вид
δL= 0; δЭ− δA= 0; (10)
здесь δ— знак вариации при изменении положения узла i.
Энергия деформации двухэлементной системы описывается урав- нениями [2]
Э= Эj−1 + Эj, (11)
2
j−1
j−1
j
j
2
j−1
j
Э= πDδтh(σ ε + σε) = πDδтhEε2 + ε2 .
Используя выражения для деформаций
ε = dw= wi− wi−1 ; ε
= wi+1 − wi, (12)
j−1 dz h j h
продолжаем преобразование выражений для Эи δЭ:
Э= πDδтhE∙1
(w− w
)2 + (w
— w)2 ; (13)
2 h2
i i−1
dЭ
i+1 i
δЭ=
dwi
δwi. (14)
Здесь варьируем только положением центрального узла при “закреп- ленных” положениях всех других узлов, поэтому в качестве перемен- ного выступает только wi:
h2
i
i−1
δЭ= πDδтhE(2w − w
— w ) δw. (15)
i+1
i
Вариация работы внешних сил при изменении положения узла i
δA= hqiδwi. (16)
Подставив выражения (15) и (16) в (10), получим
πDδтhE(2wh2 i
-
wi−1 -
wi+1
) δwi
-
hqiδwi
i
= 0;
h2
i
i+1
i−1
δтE(2w− w
— w ) − q
= 0;
wi= 2
wi−1 + wi+1 + πDδ
. (17)
1 qih2
Таким образом, формула (17) выражает условие локального равно- весия узла i(при заданных положениях других узлов).
Применяя выражение (17) последовательно ко всем узлам конечно- элементной сетки, получаем первое приближение к точному решению. Повторив многократно эту процедуру, получим второе, третье, . . . , n-е приближение. Причем, каждое последующее приближение будет ближе к точному решению.
Затем вычисляются деформация и напряжение в трубопроводе для всех i-х элементов рассматриваемого участка:
ε(i) = wi+1−wi−1 ; σ(i) = Eε(i). (18)
z 2h z z
Для примера рассмотрим задачу о продольном сдвиге грунта, вме- щающего трубопровод.
Диаметр трубопровода составляет 1220 мм, толщина стенки тру- бы — 18 мм. Температурный перепад “эксплуатация–укладка” равен
∙
∙
∙
+20 ◦С. На участке AB(см. рис. 3) произошел сдвиг грунта с коор- динатами 100. . . 160 м, сдвиг вдоль трубопровода составляет 5 м. Глу- бина залегания трубопровода 1 м. Модуль упругости материала 2,06 105 МПа; коэффициент температурного расширения материала трубы 1,2 10−5; рабочее давление в трубе 5 МПа.
Удельные веса, Н/м3: стали — 77000; нефти — 8700; изоляции —
11000; грунта — 17600. Предел текучести материала трубы 500 МПа. Коэффициент постели грунта 2,37 МПа/м; предельная реакция грунта 42700 Н/м.
Результаты расчетов приведены на рис. 7. Как следует из гра- фиков, в районе сдвига грунта основные показатели напряженно- деформированного
состояния трубопровода соответственно равны: кольцевое напряжение 164,44 МПа; максимальное смещение по оси Z
∙
6,3099 10−3 м на отметке 154 м; максимальное продольное осевое на- пряжение 129,33 МПа на отметке 149 м; максимальная интенсивность
∙
напряжений 150,00 МПа на отметке 149 м; максимальная продольная осевая деформация 6,2780 10−4 на отметке 149 м; коэффициент запаса по пределу текучести составляет 3,33.
Выводы. 1. Предложен способ автоматизированного мониторинга оползнеопасных склонов на участках прокладки трубопроводов.
-
Предложена математическая модель воздействия грунта на под- земный трубопровод на участке оползня при продольном сдвиге. -
Разработан алгоритм решения полученных уравнений и про- грамма расчета. Решение построено на основе метода конечных эле- ментов, что позволяет в процессе решения определять напряженно- деформированное состояние трубопровода.
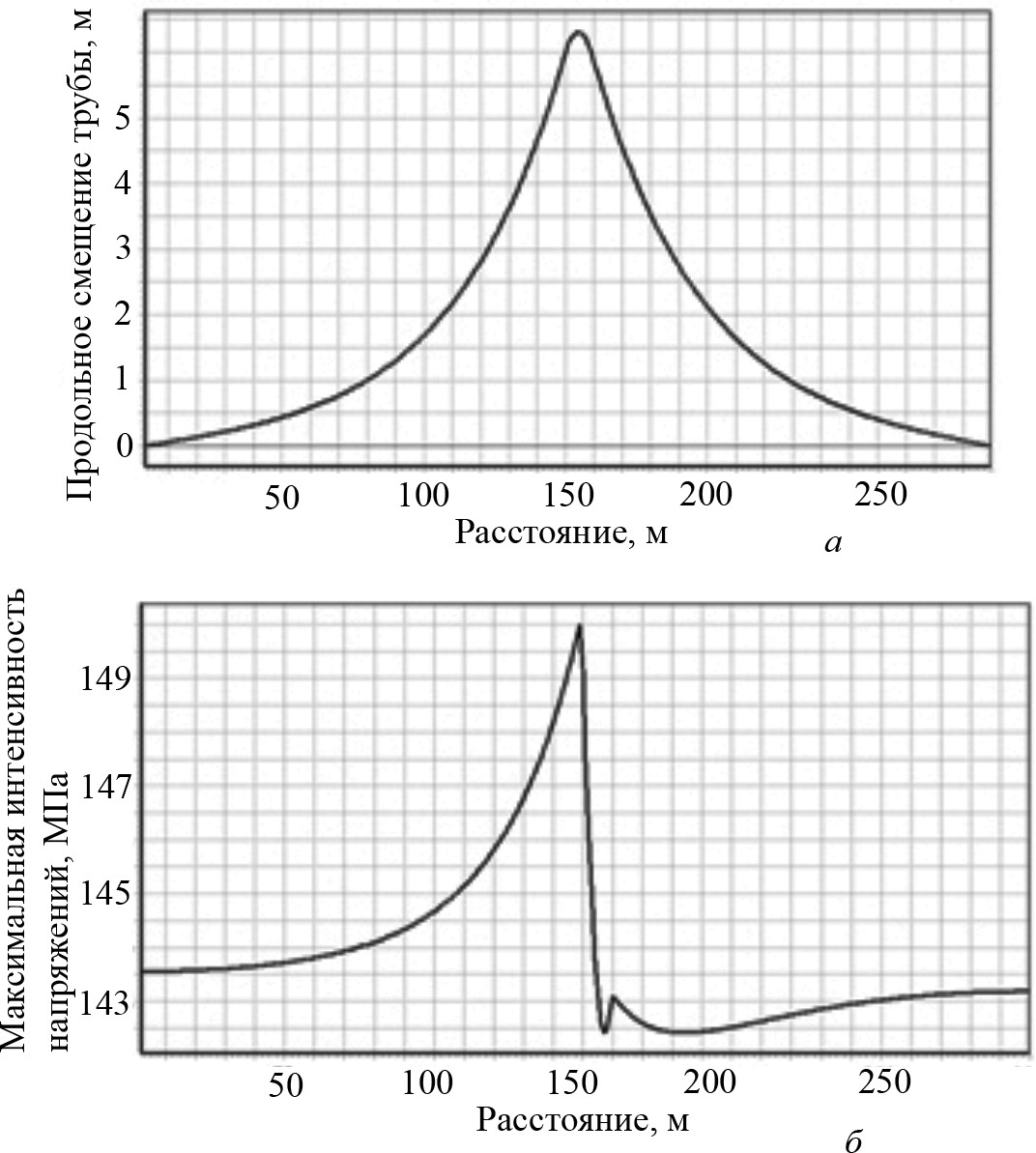
Рис. 7. Графическая зависимость продольного смещения (a) и осевой деформа- ции (б) трубы от расстояния
-
Установлено, что зона возмущения поля напряжений в трубо- проводе распространяется на несколько сот метров за пределы участка оползня.
Работа, результаты которой использованы в данной научной пу-бликации,выполненапозаказуОАО“АК“Транснефть”прифинансо-войподдержкеМинистерстваобразованияинаукиРоссийскойФеде-рации.
СПИСОК ЛИТЕРАТУРЫ
-
Ш а м м а з о в А. М., З а р и п о в Р. М., Ч и ч е л о в В. А. и др. Расчет и обеспечение прочности трубопроводов в сложных инженерно-геологических условиях. Т. 1. Численное моделирование напряженно-деформированного со- стояния и устойчивости трубопроводов. – М.: Интер. 2005. – 706 с. -
Г у м е р о в А. Г., Г у м е р о в Р. С., Г у м е р о в К. М. Безопасность дли- тельно эксплуатируемых магистральных нефтепроводов. – М.: Недра, 2001. – 305 с.
Статья поступила в редакцию 25.06.2012
Анатолий Александрович Александров окончил МВТУ им. Н.Э. Баумана в 1975 г. Д-р техн. наук, профессор, ректор МГТУ им. Н.Э. Баумана. Автор более 80 научных работ в области теории рисков, механики разрушения, промышленной безопасности и эксплуатации опасных производственных объектов.
A.A. Aleksandrov graduated from the Bauman Moscow Higher Technical School in 1975.
D. Sc. (Eng.), professor, rector of the Bauman Moscow State Technical University. Author of more than 80 publications in the field of theory of risks, fracture mechanics, industrial safety and exploitation of dangerous industrial objects.
Сергей Петрович Сущев в 1981 г. окончил МВТУ им. Н.Э. Баумана. Д-р техн. наук, профессор, директор Научно-образовательного центра исследований экстремальных ситуаций МГТУ им. Н.Э. Баумана. Автор более 100 научных работ в области теории рисков, механики разрушения, промышленной безопасности и эксплуатации опас- ных производственных объектов.
S.P. Sushchev graduated from the Bauman Moscow Higher Technical School in 1981.
D. Sc. (Eng.), professor, director of the Scientific and Educational Center of Extremal Situation Study of the Bauman Moscow State Technical University. Author of more than 100 publications in the field of theory of risks, fracture mechanics, industrial safety and exploitation of dangerous industrial objects.
Павел Александрович Ревель-Муроз в 2000 г. окончил Уфимский государственный нефтяной технический университет. Вице-президент ОАО “АК “Транснефть”
P.A. Revel’-Muroz graduated from the Ufa State Oil Technical University. Vice-president of OAO “AK Transneft”.
Данил Юрьевич Грязнев в 2009 г. окончил Российский государственный социальный университет. Младший научный сотрудник Научно-образовательного центра иссле- дований экстремальных ситуаций МГТУ им. Н.Э. Баумана. Автор более 15 научных работ в области промышленной безопасности и эксплуатации опасных производ- ственных объектов.