Файл: Разработка системы оптической накачки твердотельного лазера.doc
Добавлен: 23.11.2023
Просмотров: 42
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис.1.5 Зависимость к.п.д. ксеноновой лампы от электрической энергии, запасенной в конденсаторе.
Кривая 1 соответствует случаю, когда изменение энергии осуществляется путем изменения напряжения на конденсаторе V0, а емкость его остается постоянной (С = 700 мкф). Кривая 2 получена при фиксированном напряжении (V0 = 1400 В) и переменной емкости. Характерным для обеих кривых является наличие максимума эффективности, который достигается при энергии около 600 Дж. При фиксированной энергии вспышки эффективность лампы существенно зависит от режима питания, причем с увеличением емкости конденсатора к.п.д. возрастает (рисунок 6)
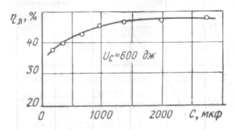
Рисунок 6- Зависимость к.п.д. лампы-вспышки от емкости конденсатора
Интенсивность излучения в сине-зеленом участке спектра, представляющем интерес для накачки многих оптических генераторов, оказывается максимальной при емкости конденсатора порядка 100 мкф.
При увеличении энергии вспышки происходит относительное увеличение эффективности лампы в коротковолновой части спектра. Это хорошо видно из рисунок 7 на котором представлены кривые спектрального распределения излучаемой энергии (в относительных единицах) для лампы ИФП-800.
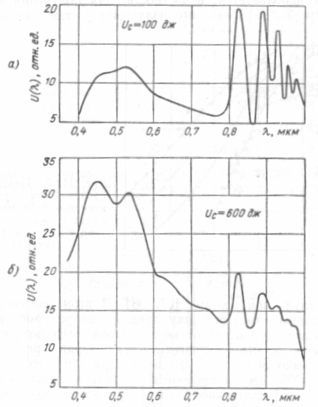
Рисунок 7- Спектр излучения лампы ИФП-800
Как следует из этих кривых, спектр излучения лампы представляет собой наложение линий и сплошного фона. Фон выражен особенно сильно в видимой и ультрафиолетовой частях спектра. В области 0,8-1,0 мкм излучаются сильные линии ксенона. При небольших уровнях энергии на долю этих линий приходится значительная часть излучения (а). По мере повышения энергии вспышки происходит увеличение плотности разрядного тока и температуры канала импульсного разряда. Это сопровождается увеличением поглощательной способности разрядной плазмы, и поэтому характер излучения лампы приближается к закону излучения абсолютно черного тела (б).
Зависимость прозрачности разряда ксеноновой лампы-вспышки от плотности разрядного тока и длины волны излучения представлены на рисунок 8
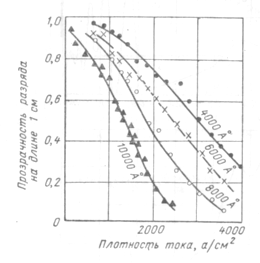
Рисунок 8- Зависимость прозрачности разряда ксеноновой лампы на длине 1 см от плотности тока и длины волны излучения
С увеличением емкости конденсатора разрядный ток (а, следовательно, и температура плазмы) уменьшается, и спектр излучения сдвигается в сторону более длинных волн.
При малых емкостях и коротких длительностях импульса плотность тока оказывается большой, и возрастает доля излучения в коротковолновых областях спектра. Этот эффект используется, в частности, для получения интенсивного ультрафиолетового излучения в так называемом двухимпульсном режиме. В этом режиме через ксеноновую лампу-вспышку предварительно пропускается ток около 2000 а/см2 от конденсатора емкостью порядка 200 мкф, а затем осуществляется разряд конденсатора малой емкости (порядка 10 мкф). При энергиях вспышки около 200 Дж достигаются импульсы тока порядка 25000 а/см2 длительностью в несколько микросекунд, что приводит к интенсивному излучению в ультрафиолетовом диапазоне. Предварительный разряд предотвращает разрушение баллона лампы ударной волной в течение короткого импульса.
Зависимость интенсивности излучения различных длин волн (в максимуме импульса) от плотности разрядного тока представлена на рисунок 9.
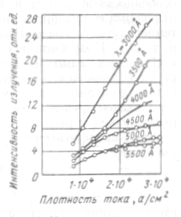
Рисунок 9- Зависимость интенсивности излучения от плотности разрядного тока
Отметим, что лампы непрерывного режима работают при сравнительно низких плотностях тока, при которых разрядная плазма практически прозрачна. Поэтому их спектр определяется главным образом линиями излучения используемого газа.
Важными характеристиками импульсных ламп накачки являются предельная энергия вспышки и средняя потребляемая мощность, при превышении которых лампа выходит из строя (разрушение баллона, повреждение электрода и т. д.). эти параметры определяются конструктивными особенностями лампы и в значительной степени зависят от режима ее питания и внешних воздействий (окружающая температура, условия охлаждения, механические нагрузки и т. д.).
1.3. СИСТЕМЫ НАКАЧКИ
Излученная источником накачки световая энергия должна быть с минимальными потерями передана в активный образец. Высокая эффективность передачи энергии достигается путем использования различного типа отражающих и фокусирующих устройств, которые в дальнейшем будут называться системами накачки. Очевидно, что от эффективности выбранной системы накачки в прямой зависимости находится коэффициент полезного действия всего генератора в целом, поэтому вопросам рационального конструирования их уделяется большое внимание.
В первых образцах оптических генераторов применялись газоразрядные лампы спиральной формы, внутри которых располагался активный образец, а снаружи диффузный цилиндрический отражатель, показанный на рисунок 10.
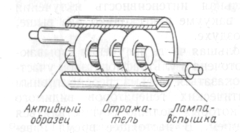
Рисунок 10 - Система накачки с лампой спиральной формы
Эффективность такой системы относительно невысока, и большая часть излученной энергии рассеивается вне образца. Для сравнительной оценки эффективности различных систем накачки удобно исходить из пороговой величины мощности или энергии возбуждения, при которой возникает генерация в определенном активном образце. Вследствие низкой эффективности оптические генераторы и усилители со спиральными лампами применяются в основном в лабораторных условиях, когда вопросы экономичности являются второстепенными и когда частота вспышек мала.
Значительно большей эффективностью обладают системы, в которых используется фокусировка излучения на активном образце. Примером такой системы служит эллиптический рефлектор, представляющий собой цилиндр эллиптического сечения, внутри которого вдоль фокусных линий размещены активный образец и лампа.
Эллипс, как известно, имеет два фокуса, причем все лучи, исходящие из одного из них, собираются во втором фокусе. Поэтому излученная лампой световая энергия концентрируется эллиптическим отражателем в месте расположения образца. Поскольку в действительности лампа не является бесконечно тонкой, а имеет конечные поперечные размеры, то, строго говоря, через вторую фокальную линию будут проходить лишь лучи, проекция которых на поперечное сечение цилиндра перпендикулярна поверхности лампы. Другие лучи фокусируются неточно, и, следовательно, изображение лампы занимает некоторую область вблизи фокальной линии. Если диаметр активного элемента превышает поперечные размеры изображения источника, то эффективность системы будет максимальной. В противном случае часть лучей на образец не попадает.
Таким образом, эффективность эллиптической системы зависит от поперечных размеров источников накачки, активного элемента и отражателя. Кроме того, как легко видеть, она определяется также эксцентриситетом эллипса, поскольку уменьшение последнего улучшает фокусировку.
Расчетная часть
2.1.Задание на курсовой проект
Радиус активного элемента Rакт. эл. =R1=4 мм
Радиус лампы Rлампы =R2=7 мм
Эксцентриситет e = 0,65
Длина большой полуоси эллипса a = 26 мм
2.2. Расчет эллиптической системы накачки
Схематическое изображение рассматриваемой системы представлено на рисунок 11.
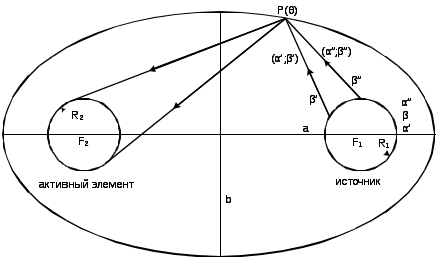
Рисунок 11- Ход лучей в эллиптическом рефлекторе
Здесь а – длина большой полуоси эллипса, R1 и R2 – радиусы источника накачки и активного образца. Любой луч, исходящий с поверхности источника, характеризуется двумя параметрами α (угловое положение начальной точки луча на контуре источника) и β (угол между направлением луча и нормалью к излучающей поверхности). Функция G(α,β) равна единице в том случае, когда луч с параметрами α,β попадает в активный образец после однократного отражения от эллипса и минуя источник. Определим границы области, в которой G(α,β) = 1.
Для того, чтобы определить границы области, в которой G(α,β) = 1, сделаем следующие построения. Из фокуса
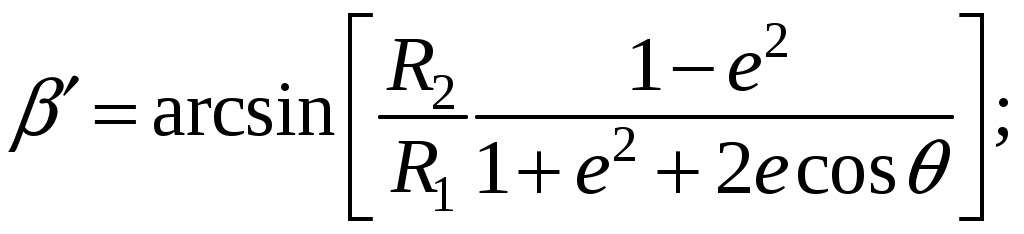 (1)
(1)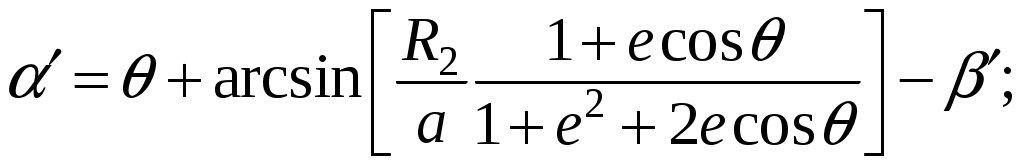
(3)
где
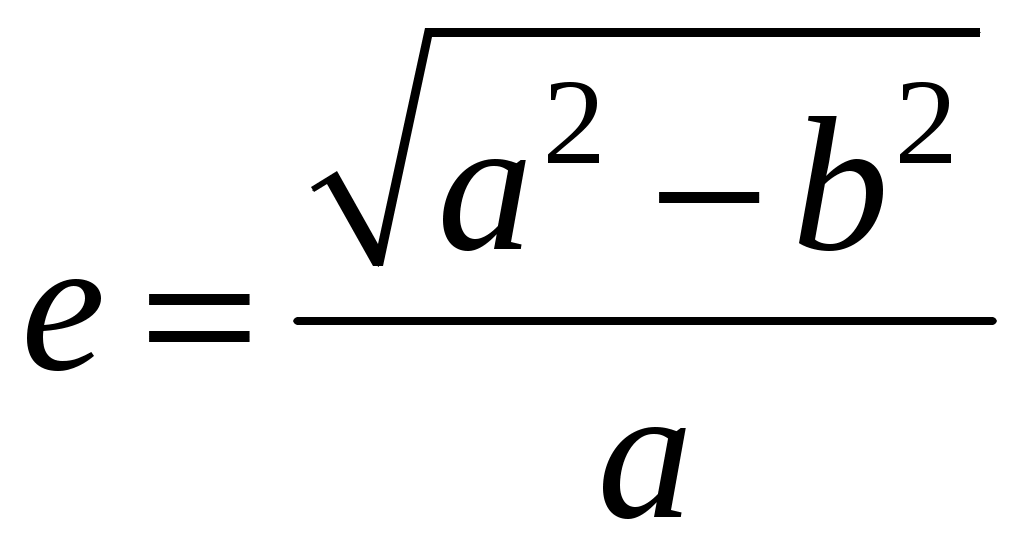 – эксцентриситет эллипса (а- большая полуось эллипса, b- малая полуось эллипса).
– эксцентриситет эллипса (а- большая полуось эллипса, b- малая полуось эллипса).Если для некоторого угла
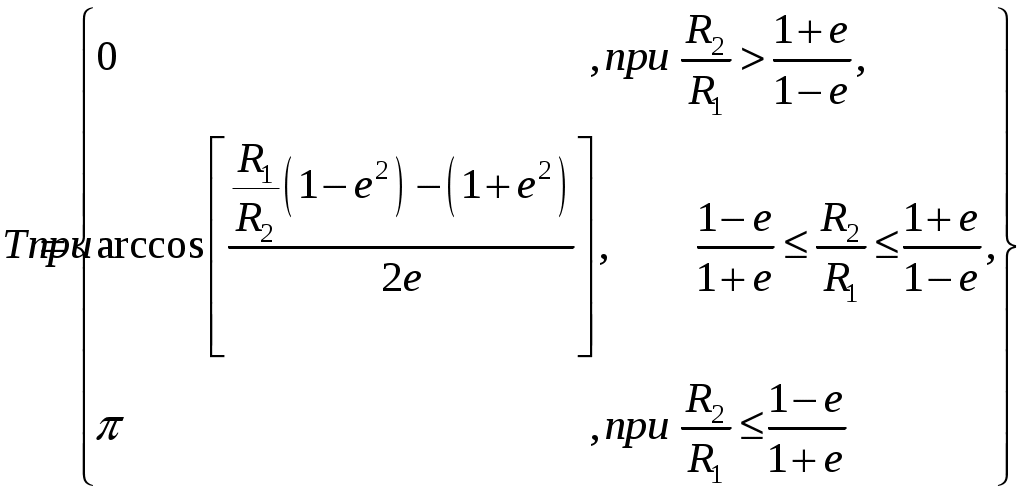 (5)
(5)Определим, какое из выражений подходит для расчета, исходя из заданных размеров:
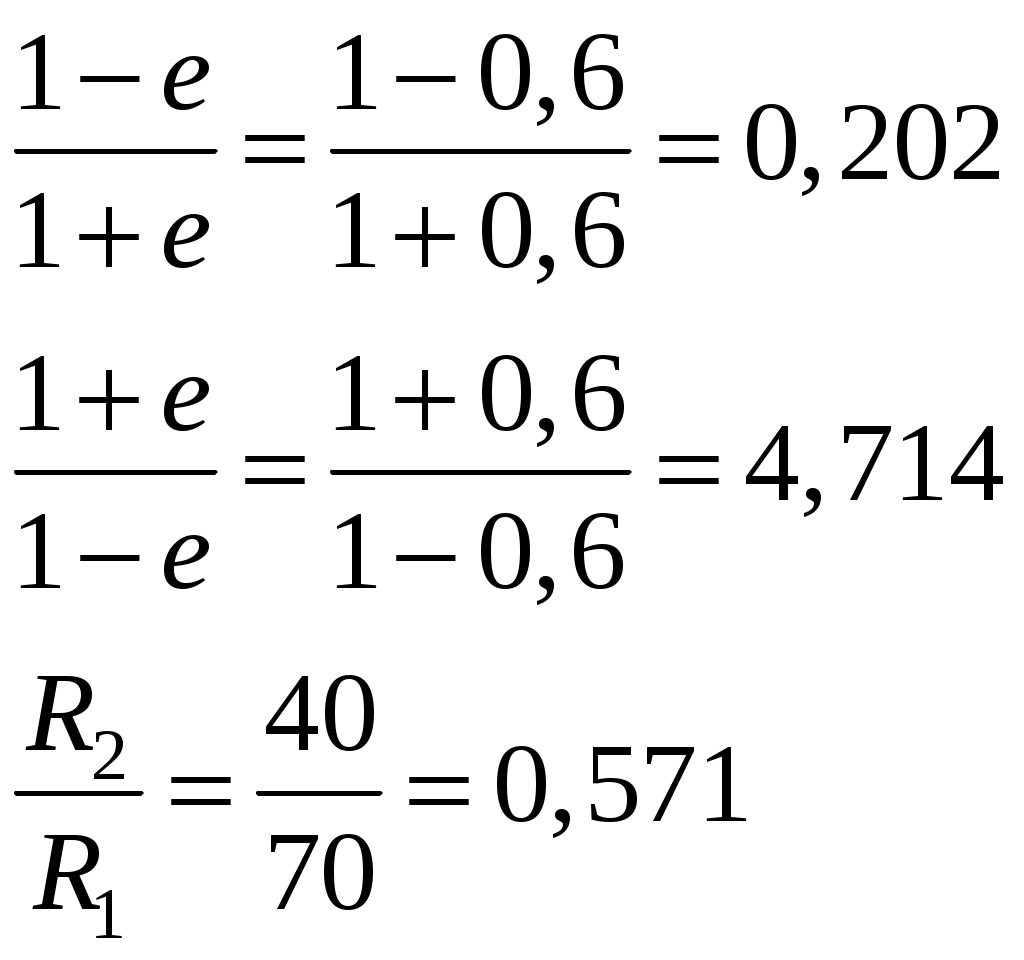
Таким образом,
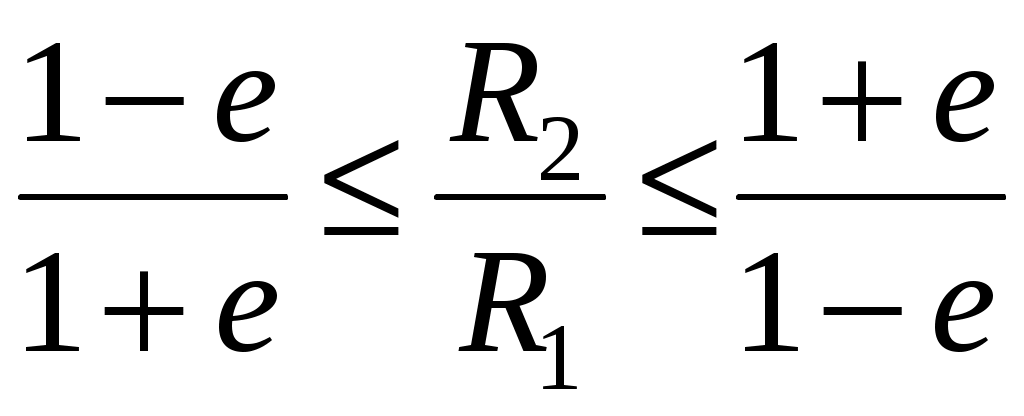 . Вычислим величину T:
. Вычислим величину T: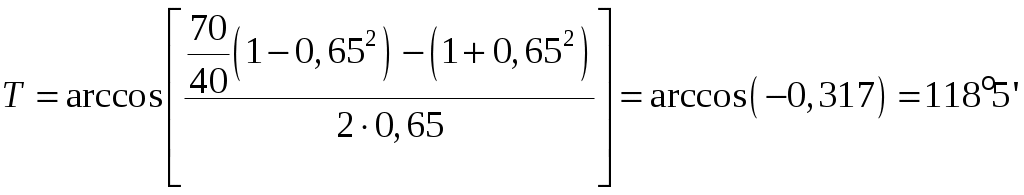
Следовательно, значения θ заключены в интервале
Таблица 1.
| θ,град | | | | |
| 0 | 6,962 | -6,962 | -1,612 | 1,612 |
| 10 | 7,013 | -7,013 | 8,359 | 11,672 |
| 20 | 7,17 | -7,17 | 18,238 | 21,823 |
| 30 | 7,442 | -7,442 | 28,018 | 32,074 |
| 40 | 7,846 | -7,846 | 37,684 | 42,438 |
| 50 | 8,408 | -8,408 | 47,212 | 52,941 |
| 60 | 9,17 | -9,17 | 56,567 | 63,616 |
| 70 | 10,193 | -10,193 | 65,696 | 74,518 |
| 80 | 11,569 | -11,569 | 74,518 | 85,726 |
| 90 | 13,444 | -13,444 | 82,906 | 97,369 |
| 100 | 16,054 | -16,054 | 90,654 | 109,652 |
| | 19,058 | -19,058 | 96,356 | 120,587 |