ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 13
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1
КОД:
using System;
class MainClass {
public static void Main (string[] args) {
int[,] a = new int[,] {
{ 36, 36, 47, 37, 44, 41, 58 },
{ 28, 47, 43, 42, 49, 49, 60 },
{ 23, 23, 36, 35, 39, 42, 56 },
{ 17, 23, 23, 11, 23, 23, 23 },
{ 23, 35, 34, 27, 48, 48, 62 },
{ 23, 29, 25, 24, 25, 42, 56 },
{ 23, 42, 47, 37, 41, 35, 80 }
};
int n = a.GetLength(0);
int m = a.GetLength(1);
int[] u = new int[n];
int[] v = new int[m];
int[] p = new int[m];
int[] way = new int[m];
for (int i = 1; i < n; ++i) {
p[0] = i;
int j0 = 0;
int[] minv = new int[m];
bool[] used = new bool[m];
for (int j = 1; j < m; ++j) {
minv[j] = int.MaxValue;
}
do {
used[j0] = true;
int i0 = p[j0];
int delta = int.MaxValue;
int j1 = 0;
for (int j = 1; j < m; ++j) {
if (!used[j]) {
int cur = a[i0, j] - u[i0] - v[j];
if (cur < minv[j]) {
minv[j] = cur;
way[j] = j0;
}
if (minv[j] < delta) {
delta = minv[j];
j1 = j;
}
}
}
for (int j = 0; j < m; ++j) {
if (used[j]) {
u[p[j]] += delta;
v[j] -= delta;
} else {
minv[j] -= delta;
}
}
j0 = j1;
} while (p[j0] != 0);
do {
int j1 = way[j0];
p[j0] = p[j1];
j0 = j1;
} while (j0 != 0);
}
int[] ans = new int[n];
for (int j = 1; j < m; ++j) {
if (p[j] != 0) {
ans[p[j] - 1] = j;
}
}
int sum = 0;
for (int i = 0; i < n; ++i) {
int j = ans[i];
if (j >= 0) {
sum += a[i, j];
}
}
Console.WriteLine("Optimal assignments:");
for (int i = 0; i < n; i++) {
Console.WriteLine("Job " + (i + 1) + " assigned to worker " + (ans[i] + 1));
}
Console.WriteLine("Total cost: " + sum);
}
}
Вывод:
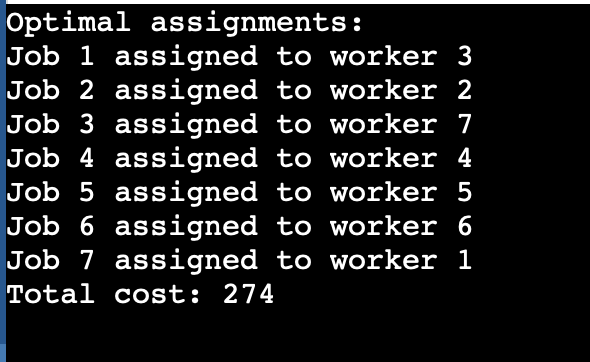
Задание 2
КОД:
using System;
using System.Collections.Generic;
using System.Linq;
namespace FactoringAlgorithms
{
class Program
{
static void Main(string[] args)
{
int number = 123456789; // число, которое нужно разложить на множители
Console.WriteLine($"Разложение числа {number} на множители:");
// Метод Ферма
var fermatStart = DateTime.Now; // засекаем время начала работы метода Ферма
var fermatFactors = FermatMethod(number);
var fermatEnd = DateTime.Now; // засекаем время окончания работы метода Ферма
Console.WriteLine($"Метод Ферма: {string.Join(" * ", fermatFactors)}, время выполнения: {(fermatEnd - fermatStart).TotalMilliseconds} мс");
// Метод Диксона
var dixonStart = DateTime.Now; // засекаем время начала работы метода Диксона
var dixonFactors = DixonMethod(number);
var dixonEnd = DateTime.Now; // засекаем время окончания работы метода Диксона
Console.WriteLine($"Метод Диксона: {string.Join(" * ", dixonFactors)}, время выполнения: {(dixonEnd - dixonStart).TotalMilliseconds} мс");
// Метод Ленстры
var lenstraStart = DateTime.Now; // засекаем время начала работы метода Ленстры
var lenstraFactors = LenstraMethod(number);
var lenstraEnd = DateTime.Now; // засекаем время окончания работы метода Ленстры
Console.WriteLine($"Метод Ленстры: {string.Join(" * ", lenstraFactors)}, время выполнения: {(lenstraEnd - lenstraStart).TotalMilliseconds} мс");
// Метод решета квадратичного
var quadraticSieveStart = DateTime.Now; // засекаем время начала работы метода решета квадратичного
var quadraticSieveFactors = QuadraticSieveMethod(number);
var quadraticSieveEnd = DateTime.Now; // засекаем время окончания работы метода решета квадратичного
Console.WriteLine($"Метод решета квадратичного: {string.Join(" * ", quadraticSieveFactors)}, время выполнения: {(quadraticSieveEnd - quadraticSieveStart).TotalMilliseconds} мс");
Console.ReadKey();
}
// Метод Ферма
static int[] FermatMethod(int n)
{
if (n <= 0)
throw new ArgumentException("Число должно быть положительным");
if (n == 1)
return new int[] { 1 };
if (n % 2 == 0)
return new int[] { 2 }.Concat(FermatMethod(n / 2)).ToArray();
int a = (int)Math.Ceiling(Math.Sqrt(n));
int b = 0;
int b2 = a * a - n;
while (!IsSquare(b2))
{
a++;
b2 = a * a - n;
}
b = (int)Math.Sqrt(b2);
return new int[] { a - b, a + b };
}
// Метод Диксона
static int[] DixonMethod(int n)
{
if (n <= 0)
throw new ArgumentException("Число должно быть положительным");
if (n == 1)
return new int[] { 1 };
int x = 2;
int y = 2;
int d = 1;
int i = 1;
while (d == 1)
{
x = (x * x + 1) % n;
y = ((y * y + 1) % n * (y * y + 1) % n + 1) % n;
d = Gcd(Math.Abs(x - y), n);
i++;
}
return d == n ? new int[] { } : new int[] { d, n / d };
}
// Метод Ленстры
static int[] LenstraMethod(int n)
{
if (n <= 0)
throw new ArgumentException("Число должно быть положительным");
if (n == 1)
return new int[] { 1 };
int a = 2;
int b = 2;
int d = 1;
var primes = GetPrimes(1000);
int i = 0;
while (d == 1)
{
a = (a * a + b) % n;
b = (b * b + 1) % n;
d = Gcd(Math.Abs(a - b), n);
if (i == primes.Count - 1)
{
i = -1;
primes = GetPrimes(primes.Last() * 2);
}
i++;
}
return d == n ? new int[] { } : new int[] { d, n / d };
}
// Метод решета квадратичного
static int[] QuadraticSieveMethod(int n)
{
if (n <= 0)
throw new ArgumentException("Число должно быть положительным");
if (n == 1)
return new int[] { 1 };
int maxFactorBase = (int)Math.Exp(Math.Sqrt(Math.Log(n) * Math.Log(Math.Log(n))));
var factorBase = GetPrimes(maxFactorBase).ToArray();
var sieve = new List
foreach (int p in factorBase)
{
int exp = 0;
while (n % p == 0)
{
n /= p;
exp++;
}
if (exp > 0)
sieve.Add(new int[] { p, exp });
}
var primes = factorBase.Take(sieve.Count).ToArray();
var exponents = new int[sieve.Count];
var matrix = new List
for (int i = 0; i < sieve.Count; i++)
{
exponents[i] = sieve[i][1];
var row = new List
int k = 0;
for (int j = 0; j < primes.Length && k < sieve[i][1]; j++)
{
int l = 0;
while (sieve[i][0] % primes[j] == 0)
{
l++;
sieve[i][0] /= primes[j];
}
row.Add(l % 2);
k += l;
}
matrix.Add(row.ToArray());
}
var indices = GaussianElimination(matrix.ToArray());
int a = 1;
for (int i = 0; i < indices.Length; i++)
{
if (indices[i])
a = (a * primes[i]) % n;
}
int b2 = a * a - n;
while (!IsSquare(b2))
{
a++;
b2 = a * a - n;
}
int b = (int)Math.Sqrt(b2);
return new int[] { a - b, a + b };
}
// Проверка, является ли число квадратом целого числа
static bool IsSquare(int n)
{
int sqrt = (int)Math.Sqrt(n);
return sqrt * sqrt == n;
}
// Нахождение НОД двух чисел
static int Gcd(int a, int b)
{
if (b == 0)
return a;
return Gcd(b, a % b);
}
// Получение списка простых чисел до заданного числа
static List
{
var primes = new List
for (int i = 2; i <= n; i++)
{
bool isPrime = true;
for (int j = 2; j <= Math.Sqrt(i); j++)
{
if (i % j == 0)
{
isPrime = false;
break;
}
}
if (isPrime)
primes.Add(i);
}
return primes;
}
// Решение системы линейных уравнений методом Гаусса
static bool[] GaussianElimination(int[][] matrix)
{
int rows = matrix.Length;
int cols = matrix[0].Length;
bool[] result = new bool[cols];
for (int i = 0; i < cols; i++)
{
for (int j = i; j < rows; j++)
{
if (matrix[j][i] != 0)
{
int[] temp = matrix[j];
matrix[j] = matrix[i];
matrix[i] = temp;
break;
}
}
if (matrix[i][i] == 0)
continue;
for (int j = i + 1; j < rows; j++)
{
if (matrix[j][i] == 0)
continue;
for (int k = i; k < cols; k++)
{
matrix[j][k] = (matrix[j][k] * matrix[i][i] - matrix[i][k] * matrix[j][i]) / Gcd(matrix[i][i], matrix[j][i]);
}
}
}
for (int i = cols - 1; i >= 0; i--)
{
if (matrix[i][i] == 0)
continue;
int gcd = matrix[i][i];
for (int j = i - 1; j >= 0; j--)
{
if (matrix[j][i] == 0)
continue;
gcd = Gcd(gcd, matrix[j][i]);
}
result[i] = (gcd == matrix[i][i]);
}
return result;
}
}
}
Вывод:
