МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА - Российский технологический университет» РТУ МИРЭА
Институт искусственного интеллекта
Кафедра автоматических систем
Лабораторная работа №3 по дисциплине «Цифровая обработка сигналов (Часть 2/2)» На тему: «Исследование рекурсивных цифровых фильтров»

Выполнил

студент группы КТСО-03-19 Новоселов А.И.

Приняла Гурьянова Е.О.

Москва 2023

Лабораторная работа 3.

ИССЛЕДОВАНИЕ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ.

ВАРИАНТ 19.

Целью работы является изучение метода определения передаточной функции рекурсивного цифрового фильтра с помощью билинейного преобразования передаточной функции аналогового фильтра. Исследование частотной характеристики цифрового фильтра. Определение реакции фильтра на тестовую дискретную последовательность.

Задание

1. 
   Рассчитать передаточную функцию цифрового фильтра нижних частот 2-го порядка с заданным значениями параметров: частоты среза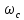 и .
   
2. 
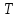   Рассчитать амплитудно-частотную характеристику цифрового фильтра по его передаточной функции в интервале частот .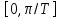
   
3. 
   Сформировать входную дискретную последовательность.
   
4. 
   По найденной передаточной функции цифрового фильтра нижних частот записать разностное уравнение фильтра и рассчитать выходную последовательность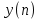 цифрового фильтра при входной последовательности .
   
5. 
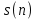   Наблюдать на экране дискретные последовательности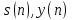 и сделать вывод о работе фильтра.
   

---

Согласно моему варианту, параметры нормированной передаточной функции фильтра имеют следующий вид:

1. 
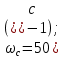
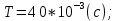
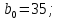
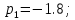
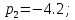
   Рассчитать передаточную функцию цифрового фильтра нижних частот 2-го порядка с заданным значениями параметров: частоты среза и .
   

Частота среза аналогового прототипа равна:



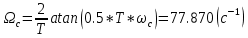
Общий вид передаточной функции:



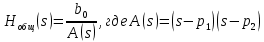
Тогда, передаточная функция принимает вид:



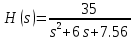
Теперь определяем передаточную функцию аналогового прототипа путем замены в передаточной функции общего вида 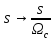, получим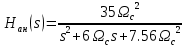



Передаточную функцию цифрового фильтра находим с использованием конформного преобразование Мёбиуса .

2. 
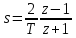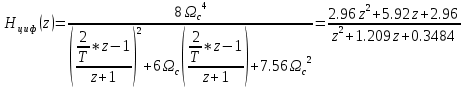
   Рассчитать амплитудно-частотную характеристику цифрового фильтра по его передаточной функции в интервале частот .
   

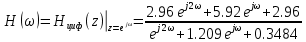, получаем

АЧХ: ;

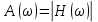ФЧХ: .


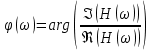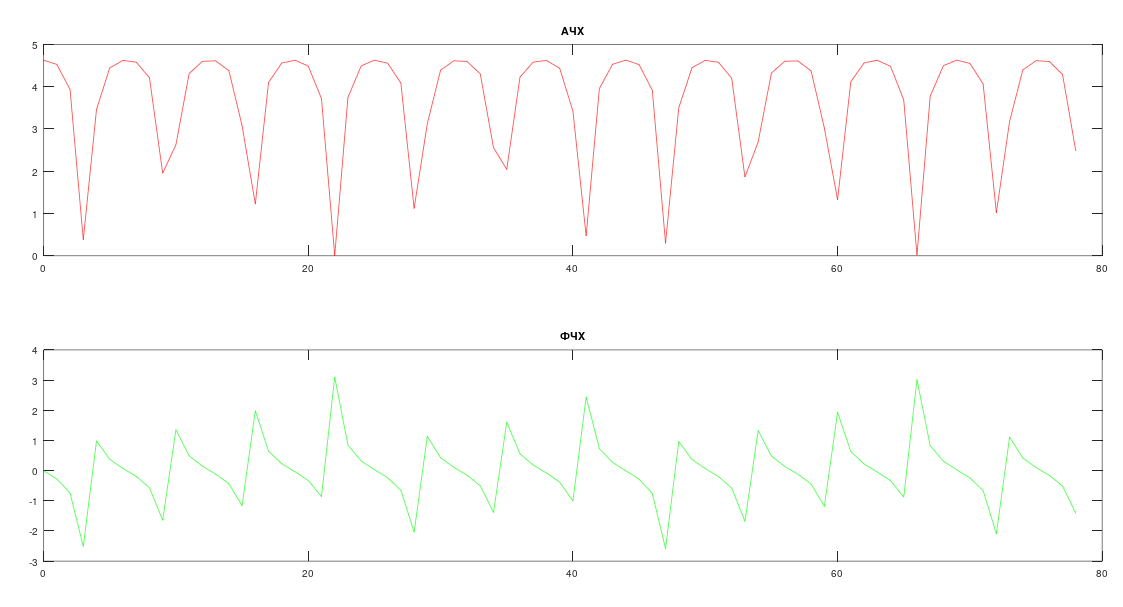
рис 1. Частотные характеристики фильтра

---

3. 
   Сформировать входную дискретную последовательность.
   

Входную дискретную последовательность формируем путем суммирования двух разночастотных гармонических последовательностей.

.

4. 
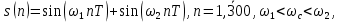
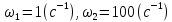   По найденной передаточной функции цифрового фильтра нижних частот записать разностное уравнение фильтра и рассчитать выходную последовательность цифрового фильтра при входной последовательности .
   

Разностное уравнение получим из передаточной функции, принимающей вид

5. 
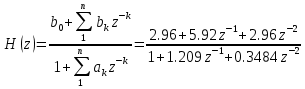
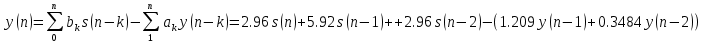
   Наблюдать на экране дискретные последовательности и сделать вывод о работе фильтра.
   

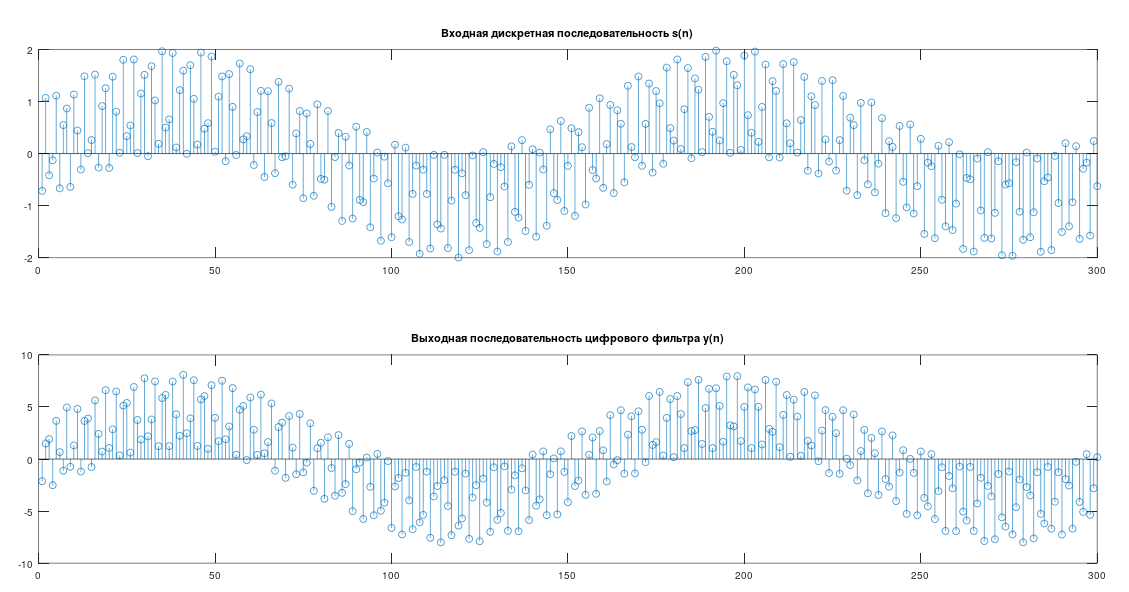
рис 2. Входная и Выходная последовательности

Полученные результаты демонстрируют, что синтезированный рекурсивный фильтр нижних частот фильтрует высокие частоты.
Вывод: в ходе выполнения лабораторной работы были изучены методы определения передаточной функции рекурсивного цифрового фильтра с помощью билинейного преобразования, были исследованы частотные характеристики цифрового фильтра, были определены реакции фильтра на тестовую дискретную последовательность.

Исходный код

pkg load signal

pkg load control
wc = 50;

T = 40 * 10^-3;

b0 = 35.0;

p1 = -1.8;

p2 = -4.2;
omega = 2 / T * tan(0.5 * T * wc);

disp('Частота среза аналогового прототипа: ');disp(omegaC);
s = tf('s');

A_s = (s - p1)*(s - p2);

H_s = b0 / A_s
#{

35

H_s: ----------------

s^2 + 6 s + 7.56

#}
#Способ 1: представление билинейного преобразования при помощи прямой замены

z = tf('z',0.1);

s = (2 / T) * ((z - 1)/(z + 1))/omegaC;

A_z = (s - p1)*(s - p2);

H_z = b0/A_z
#{

35 z^2 + 70 z + 35

H_z: -------------------------

11.82 z^2 + 14.3 z + 4.12

#}
#Способ 2: представление билинейного преобразования при помощи встроенной функции bilinear()

---

b_analog = [35*omegaC^2];

a_analog = [1 6*omegaC 7.56*omegaC^2];

[b_digital a_digital] = bilinear(b_analog, a_analog, T);

H_digital = tf(b_digital, a_digital, 0.1)
#{
2.96 z^2 + 5.92 z + 2.96

H_digital: ------------------------

z^2 + 1.209 z + 0.3484
#}
#Если привести H_z к виду sum(b_i * z^i) / ((1 + sum(a_i)) * z^i), получится результат H_digital

#Входная последовательность s(n)

wc1 = 1;

wc2 = 100;

s_n = @(n)(sin(wc1 * T * n) + sin(wc2 * T * n));
#Коэффициенты b, i

# 2.96 z^2 + 5.92 z + 2.96

# z^2 + 1.209 z + 0.3484
b = [2.96 5.92 2.96];

a = [1.209 0.3484];
#Выходная последовательность

for n = 1:1000
if n == 1

y(n) = b(1) * s_n(n);

endif

if n == 2

y(n) = b(1) * s_n(n) + b(2) * s_n(n-1) - (a(1) * y(n-1));

endif

if n > 2

y(n) = b(1) * s_n(n) + b(2) * s_n(n-1) + b(3) * s_n(n-2) - (a(1) * y(n-1) + a(2) * y(n-2));

endif
endfor
#Частотная характеристика

w_temp = @(w)(exp(j .* w));

y_w = @(w)((2.96.*w_temp(w).^2 + 5.92.*w_temp(w) + 2.96) ./ (w_temp(w).^2 + 1.209.*w_temp(w) + 0.3484));
#Графики АЧХ и ФЧХ

figure()

fr = [];

pr = [];

for n_pi = 0:pi/T

t = y_w(n_pi);

fr = [fr abs(t)];

pr = [pr arg(t)];

endfor
subplot(211)

plot([0:pi/T], fr([1:pi/T+1]), 'r')

title('АЧХ')
subplot(212)

plot([0:pi/T], pr([1:pi/T+1]), 'g')

title('ФЧХ')
#Графики входной и выходной последовательности

figure()

hold on;

subplot(211)

stem([1:300], s_n([1:300]))

title('Входная дискретная последовательность s(n)')
subplot(212)

stem([1:300], y([1:300]))

title('Выходная последовательность цифрового фильтра y(n)')

---

Смотрите также файлы

• Не содержит обозначения выделяемой субстанции термин Выберите один ответ.docx

• Практикоориентированное задание 2 Восстановите данные таблицы.docx

• Двигатель, сцепление, кп, карданные валы Проверку герметичности системы питания двигателя воздухом.docx

• Лабораторная работа 4 Решение типовых задач алгебры и анализа студент гр. Сула255ск силин И. П.docx

• Доклад по выбранной теме. 1 Отформатируйте текст 2 Создайте автооглавление текста 3 Создайте три колонки в тексте для формирования брошюры в отдельном документе.pdf