Файл: Расчет конструкции балочной клетки.docx

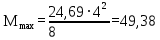кН/м.

Требуемый момент сопротивления балки настила из условия прочности на изгиб определяется по формуле 1.1.6:

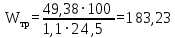см³.

По сортаменту подбираем двутавр № 20 с характеристиками: J_x= 1840 см⁴, W_x = 184 см³, вес 1 пог. м балки настила m₄ = 21,0 кг.

Проверка жёсткости (прогиба балки) по условию 6:



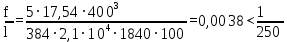
Данная балка удовлетворяет требованиям деформативности.

1.3.2 Подбор сечения вспомогательных балок для усложнённой балочной клетки №2

- нормативная нагрузка рассчитывается по формуле:

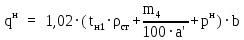(1.3.3)

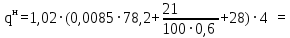118,38 кН/м;

- расчётная нагрузка рассчитывается по формуле:

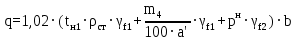(1.3.4)

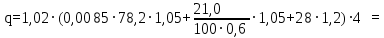141,43 кН/м.

Максимальный изгибающий момент определяется по формуле :

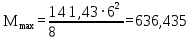кН/м.

Требуемый момент сопротивления балки из условия прочности на изгиб определяется по формуле 5:

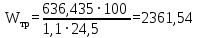см³.

По сортаменту подбираем двутавр № 60 с характеристиками: J_x= 76806 см⁴, W_x = 2560 см³, вес 1 пог. м балки настила m₄ = 108 кг.

Проверка жёсткости (прогиба балки) по условию 6:

.

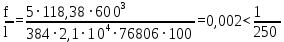Данная балка удовлетворяет требованиям деформативности.

Определяем расход материалов по УБК по формуле 14:

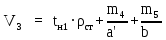(1.3.5)

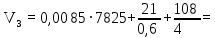128,51 кг/м².

К дальнейшей разработке принимаем вариант с меньшим расходом материала, т.е. УБК №2.

2 РАСЧЕТ И КОНСТРУИРОВАНИЕ ГЛАВНОЙ БАЛКИ

2.1 Сбор нагрузок

Главная балка проектируется в виде сварного симметричного двутавра.



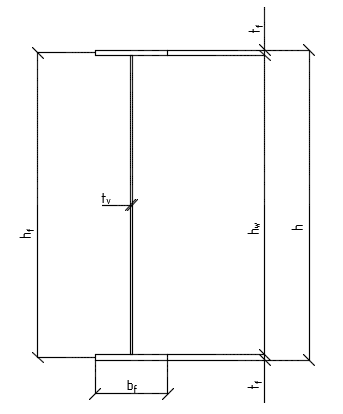
Рисунок 2.1 – Главная балка

Определим нагрузки на главную балку.

Нормативная нагрузка определяется по формуле:

---

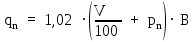(2.1.1)

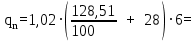179,22 кН/м

Расчетная нагрузка определяется по формуле 15:

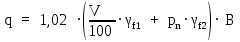(2.1.2)

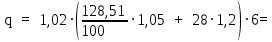213,89 кН/м

Определим максимальный изгибающий момент по формуле:

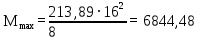кН·м

Определим максимальную поперечную силу по формуле:

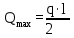(2.1.3)

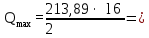1711,12 кН.

Требуемый момент сопротивления балки настила определим по формуле:

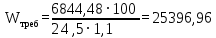см³.

2.2 Выбор высоты главной балки

Поскольку момент сопротивления балки выходит за пределы сортамента, то сечение балки проектируем составное, сварное из трех листов.



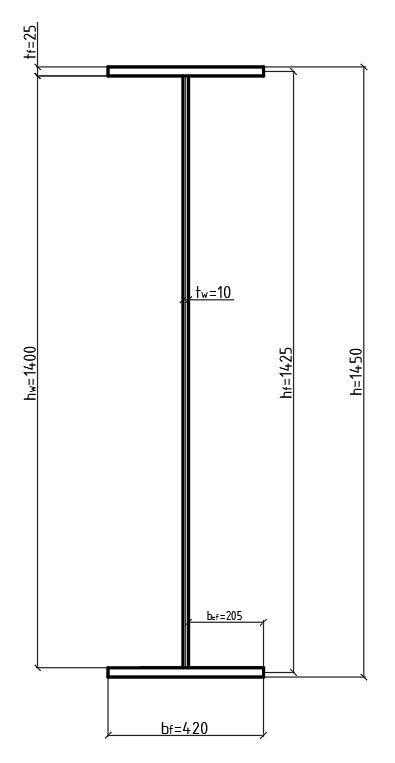
Рисунок 2.2 – Геометрические характеристики сечения главной балки

Высота главной балки определяется по двум условиям:

1. 
   h≥h_min;
   
2. 
   h≈h_opt;
   

Первое условие обеспечивает жесткость главной балки, второе условие – наименьшую материалоёмкость балки.

Минимальная высота балки определяется по формуле:

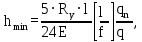(2.2.1)

где l = A – пролет главной балки;

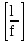– величина, обратная допустимому относительному прогибу главной балки, .

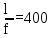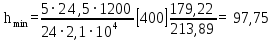см

Оптимальная высота балки из опыта проектирования определяется по формуле:

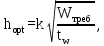(2.2.2)

где k – коэффициент для сварных балок, k = 1,1

t_w – толщина стенки, предварительно принимаем t_w = 1см.

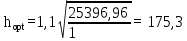см

Предварительно принимаем высоту балки по максимальной величине h=175,30 см.

---

Задаемся толщиной поясов t_f = 25 мм, тогда требуемая высота стенки определяем по формуле 19:

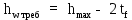(2.2.3)

h_wтреб=175,3 - 2⋅2,5=170,3 см

В соответствии с ГОСТ 19903-74* на листовую сталь ([1], п.2.6) принимаем высоту стенки h_w=1800 мм. Тогда, окончательная высота балки определяется по формуле :

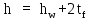(2.2.4)

h=1800+2⋅25=1850мм

2.3 Компоновка сечения

Определяем толщину стенки из условия прочности на срез по формуле :

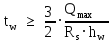(2.3.1)

где Q_max – максимальная поперечная сила в балке;

R_s – расчетное сопротивление стали срезу, R_s = 0,58∙R_y = 14,79кН/см²;

h_w– высота стенки балки, см.

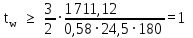см

Предварительно мы приняли толщину стенки t_w=1см, но так как при расчете на срез мы получили t_w=1 см, значит толщина стенки была принята правильно.

Определим момент инерции стенки балки по формуле:

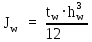(2.3.2)

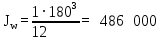см⁴

Определим требуемый момент инерции для всего сечения балки по формуле:

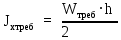; (2.3.3)

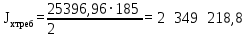см⁴

Определим требуемый момент инерции поясных листов по формуле 24:

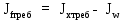; (2.3.4)

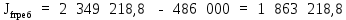см⁴

Определим требуемую площадь поясных листов по формуле 25:

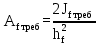, (2.3.5)

где h_f – расстояние между центрами тяжести поясных листов.

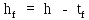; (2.3.6)

h_f=185-2,5=182,5 см

Тогда требуемая площадь поясных листов:

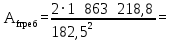111,88 см²

Определим требуемую ширину поясных листов по формуле 26:

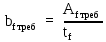; (2.3.7)

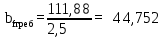см.

Окончательно требуемую ширину пояса принимаем в соответствии с ГОСТ 82-70* на листовую сталь ([2], п.2.8) (кратно 5 мм, при этом не меньше 180 мм) принимаем b

---

_f = 450мм.

Для обеспечения устойчивости пояса должны выполняться условия:

1. 
   ;
   
2. 
   ,
   

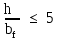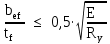где b_ef – свес пояса.

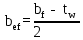; (2.3.8)

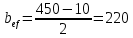мм

1. 
   ;
   
2. 
   
   

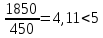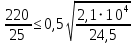
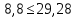
Условия выполняются, следовательно, окончательная ширина пояса 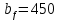мм.

Определим геометрические характеристики принятого сечения по формуле 2.3.9:

; (2.3.9)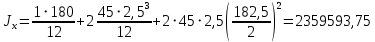

см⁴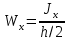

; (2.3.10)

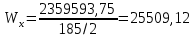см³

Прочность принятого сечения определяем по формуле 2.3.11:

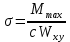; (2.3.11)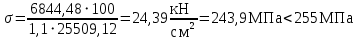



Условие прочности выполняется

---

2.4 Изменение сечения главной балки

В целях экономии материала изменением сечения балки в соответствии с эпюрой изгибающих моментов. Изменение сечения производим за счет уменьшения ширины поясов.

Изменение сечения производится на расстоянии от опоры

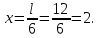
Определим изгибающий момент в месте изменения сечения по формуле 2.4.1:

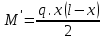; (2.4.1)

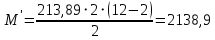кН м

Определим поперечную силу в этом сечении по формуле 2.4.2:

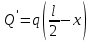; (2.4.2)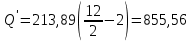



Требуемый момент сопротивления измененного сечения определяется с учетом прочности стыкового сварного шва.

Расчетное сопротивление шва определяем по формуле 2.4.3:

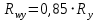; (2.4.3)

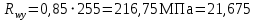кН/см²

Требуемый момент сопротивления измененного сечения определяем по формуле 2.4.4:

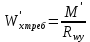; (2.4.4)

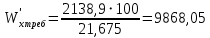см³

Определим требуемый момент инерции измененного сечения по формуле 2.4.5:

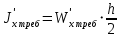; (2.4.5)

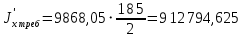см⁴

Определим требуемый момент инерции измененного пояса по формуле 2.4.6:

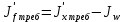; (2.4.6)

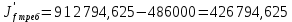см⁴

Определим требуемую ширину измененного пояса по формуле 2.4.7:

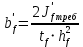; (2.4.7)

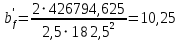см

Ширину листа принимаем по ГОСТ 82-70* ([2], п.2.8) 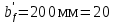см.

Должны обеспечиваться два условия:

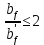1. 
   ;
   

---