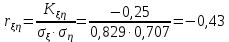1. 
   Бросают игральную кость. Путь событие А – это выпадение четного числа, а событие В – выпадение числа большего 3. Что представляют собой события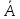 , , 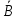AυB, A∩B, A\B, B\A? Какие элементы пространства элементарных исходов данного опыта им благоприятствуют?
   

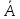– выпадение нечетного числа, {1, 3, 5}; 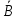– выпадение числа до 3, {1, 2, 3} ;AυB – выпадение или четного числа или числа больше 3, {2, 4, 5, 6};A∩B – выпадение четного числа и числа больше 3, {4, 6};A\B – выпадение четного числа не больше 3, {2};B\A – выпадение нечетного числа больше 3, {5}.

2. 
   Бросают две игральные кости. Найти вероятность события A, когда сумма выпавших очков равна 5, и события B, когда произведение выпавших очков равно 4.
   

Сумма очков, выпавших на двух костях, будет равна пяти в следующих случаях:если на первой кости выпадет 1, а на второй кости - 4;если на первой кости выпадет 2, а на второй кости - 3;если на первой кости выпадет 3, а на второй кости - 2;если на первой кости выпадет 4, а на второй кости - 1.Произведение очков, выпавших на двух костях, будет равно четырем в следующих случаях:если на первой кости выпадет 1, а на второй кости - 4;если на каждой из двух костей выпадет 2;если на первой кости выпадет 4, а на второй кости - 1.Когда бросают одну кость, существует шесть возможных исходов. Найдем количество исходов при бросании двух костей. Для этого составим произведение:6 * 6 = 36 (исходов).Для события А благоприятных 4 исхода, следовательно:Р (А) = 4/36 = 1/9 –вероятность события А;Для события В благоприятных 3 исхода, следовательно:Р (А) = 3/36 = 1/12 – вероятность события В.

3. 
   Случайным образом выбирают 3 шара из 8, среди которых 3 белых и 5 черных. Найти вероятность того, что среди выбранных окажется два белых шара.
   

Вероятность того, что будет вынуто 2 белых и 1 черный шар рассчитывается по формуле:

---

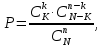
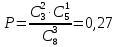
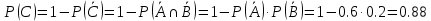
Где k – количество вытянутых белых шаров;К – общее количество белых шаров;n – количество шаров, которые вытаскивают;N – общее количество шаров.По формуле:4. Два независимых события A и B наступают с вероятностями 0,4 и 0,8 соответственно. Найти вероятность того, что наступит: а) хотя бы одно событие; б) ровно одно событие. a) Вероятность наступления хотя бы одного события равна:б) Вероятность наступления ровно одного события:

5. 
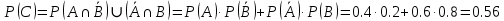
   В группе 20 студентов: 2 отличника, 8 хорошистов, 6 троечников и 4 двоечника. Отличники учат 100% экзаменационных билетов, хорошисты – только 80%, троечники – 60% и двоечники – только 40%. Найти вероятность того, что взятый наугад студент этой группы сдаст экзамен. Если некий студент данной группы сдал экзамен, то какова вероятность того, что он являлся одним из шести троечников?
   

Введём полную группу несовместных гипотез:H1 – случайно выбранный студент является отличником;H2 – случайно выбранный студент является хорошистомH3 – случайно выбранный студент является троечником;H4 – случайно выбранный студент является двоечником.P(H1) = 1/10, P(H2) = 2/5, P(H3) = 3/10, P(H4) = 1/5 – вероятности выбора отличника, хорошиста, троечника и двоечника. Р_Н1(А) = 1, Р_Н2(А) = 0,8, Р_Н3(А)=0,6, Р_Н4(А) = 0,4 – вероятность того, что отличник, хорошист, троечник и двоечник сдадут экзамен.По формуле полной вероятности найдем вероятность, что взятый наугад студент сдаст экзамен:Р = P(H1)⸳Р_Н1(А)+P(H2)ꞏР_Н2(А) +P(H3)⸳Р_Н3(А)+P(H4)ꞏР_Н4(А) = 1/10ꞏ1+2/5ꞏ0,8+3/10ꞏ0,6+1/5ꞏ0,4=34/50По формуле Байеса можно найти вероятность, что сдаст троечник:

5. 
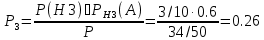
   Известна вероятность события A: p(A) = 0,3. Дискретная случайная величина ξ – число появлений события A в трех опытах. Требуется построить ряд распределения этой случайной величины, найти ее математическое ожидание M[ξ], дисперсию D[ξ], среднее квадратическое отклонение σ и вероятность попадания в интервал p(|ξ – M[ξ]| < σ).
   

---

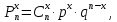
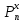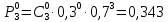
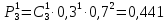
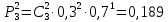
Случайная величина ξ имеет биномиальное распределение. 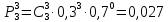Найдем закон распределения случайной величины ξ, используя формулу Бернулли:где n = 3 – всего опытов;х = ξ = {0; 1; 2; 3} – вероятное количество появления событий; – вероятность того, что n опытов появится ровно х событий;р = 0,3 – вероятность события;q = 1 - 0,3 = 0,7 – вероятность обратного события.При ξ = 0:При х ξ = 1:При х ξ = 2:При ξ = 3:Закон распределения:

ξ	0	1	2	3
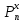	0,343	0,441	0,189	0,027

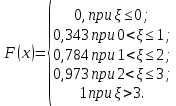
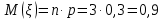
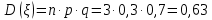
Проверка: 0,343+0,441+0,189+0,027=1Функция распределения:Математическое ожидание:Дисперсия:Среднее квадратичное отклонение:

5. 
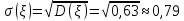
   Дана плотность распределения вероятности непрерывной случайной величины ξ
   

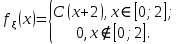
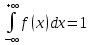
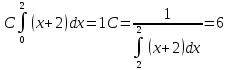
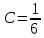
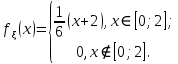
Найти значение константы С, функцию распределения F_ξ(x), вероятностьпопадания в интервал p(ξ∈[1, 3]), математическое ожидание M[ξ] и дисперсию D[ξ]. Функция плотности распределения вероятности обладает свойством:В данном случае:Функция плотности распределения:Найдите функцию распределения F(x):Если

---

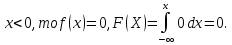
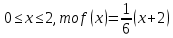
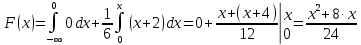
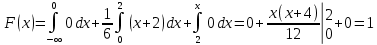
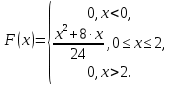
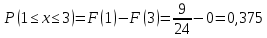
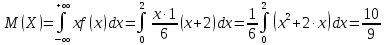
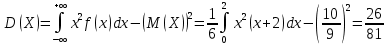
Если Если x>2, то f(x)=0Таким образом, искомая функция распределения:Вычислить вероятности попадания значений случайной величины Х на промежуток [1;3]:Математическое ожидание:Дисперсия:8. Случайная величина ξ имеет нормальное распределение с математическим ожиданием a = 15 и дисперсией σ² = 400. Найти интервал, симметричный относительно математического ожидания, вероятность попадания в который равна p=0,8859. 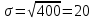Среднее квадратичное отклонение:Будем искать интервал в виде а±tꞏ σ. Тогда по условию 0,8859 = 2Ф(t). Обратимся к таблице значений функции Лапласа. Найдем значение аргумента, при котором функция Ф(t) = 0,44295. В результате получим t = 1,58.Интервал:

5. 
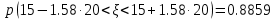
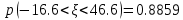
   Дан ряд распределения двумерной случайной величины (ξ, η):
   

ξ, ƞ	0	1	2
-1	1/8	0	P13
0	1/8	1/8	0
1	3/8	1/8	0

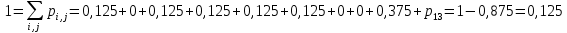
Найти значение p₁₃, частные распределения случайных величин ξ и η, их математическое ожидание и дисперсию (т.е. M[ξ], D[ξ], M[η], D[η]), а также корреляционный момент K_ξ,η и коэффициент корреляции r_ξ,η.Вероятность попадания случайной точки с координатами (ξ, η) в область G вычисляется по формуле:P₁₃ =0,125.Определение частных распределений. При известном совместном распределении систем двух дискретных случайных величин (ξ, η) частные распределения находятся по формулам:

---

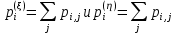
Полученные частные ряды распределения:

ξ	0	1	2
p	0,625	0,25	0,125

ƞ	-1	0	1
p	0,25	0,25	0,5

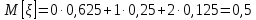
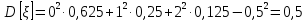
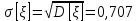
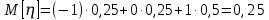
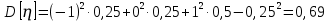
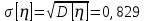
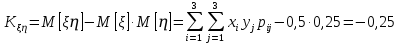
Математическое ожидание M[ξ]:Дисперсия D[ξ]:Среднее квадратическое отклонение σ[ξ]:Математическое ожидание M[ƞ]:Дисперсия D[ƞ]:Среднее квадратическое отклонение σ[ƞ]:Корреляционный момент случайных величин ξ и η:Коэффициент корреляции r_ξ,η:

---

Смотрите также файлы

• Эффективное управления предприятием как фактор повышения его конкурентоспособности.docx

• Задача Подобрать расчетным путем оборудования для эксплуатации скважины установкой электроцентробежного насоса (уэцн) и определить удельный расход электроэнергии при ее работе.docx

• 6. Электрически станции на возобновляемых источниках энергии. Ветряные электрические станции схемы работы и схемы электрических соединений вэс.pdf

• Цель дипломной работы повышение коэффициента нефтеотдачи на примере разработки Соколовского месторождения.docx

• Громкоговорителя, если собственная частота системы 35 Гц, а частота электрических колебаний, подводимых к звуковой катушке 835 Гц Чем управляются колебания подвижной системы.doc