ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИФедеральное государственное образовательное бюджетное учреждениевысшего профессионального образования«Санкт-Петербургский государственный университет телекоммуникацийим. проф. М. А. Бонч-Бруевича»Факультет Институт непрерывного образованияКонтрольная работапо дисциплине «Математика»«Вариант №2»Выполнил:студент группы______ФИО_______________Курс _____ Санкт-Петербург 2022 г1. Решить систему методом Гаусса1) 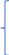x₁ + 2x₂ – x₃ + 3x₄ = - 12x₁ – x₂ + x ₃– x₃ = - 9-x₁ + 3x₂ + 4x₃ = 2

A=		1 2 −1 3 2 −1 1 −1 −1 3 4 0
b=				−1 −9 2

---

Ответ:x₁ = -18/5 – 1/3 * λ₁x₂ = 4/5 – 1 * λ₁x₃ = -1 + 2/3 * λ₁x₄ =λ₁2. Найти обратную матрицу А^-1 11) 1 1 2А = 2 -1 24 1 4 -1 -1/3 2/3А^-1 = 0 -2/3 1/3

1. 
   1/2 -1/2
   

3. В задачах 21-30 найти, при каких действительных x и y справедливо равенство, если z = x + iy21)(1-2i)²+(4-3i/2-i)= iz +2i^-94 + (1 – 2i)² – 5i/2 = iz + 2i^-9(1 – 2i)^2 – 5i/2 = iz – 4 – 2iz = -4 – 2i +iz / (((1-2i)² – 5i/2) / z)Ответ: z = -9/2 – i4. В задачах 31-40 найти производную данных функций. Результат не упрощать.31)a) y = 2 + 4e^-x + tg(x/5) + arctg(3x)tan²(x)/5 + 1/5 – 3/9x²+1 – (4e)^-x log(4e)б) y = (x)^1/3*arccos⁴(x) + 5ln(1 – x²) + (x)^1/2- 4(x)^1/3 acos³(x) / (1 – x)^1/2 – 10x / 1 – x² + 1 / 2(x)^1/2 + acos⁴(x) / 3(x)^2/3в) y = (x)⁵ / (3 +(2)^x) + 1 / (7-2x)^1/2- 2^x x⁵ log(2) / (2^x + 3)² + 5x⁴ / 2^x + 3 + 1 / (7 – 2x)^1/2 * (7 – 2x)5. В задачах 41-50 используя правило Лопиталя, найти пределы.41)Lim_x->0 e^7x – e^-2x / sin(x) – 2x Ответ: Lim_x->0 e^7x – e^-2x / sin(x) – 2x = - 96. В задачах 51-60 исследовать функцию методами дифференциального исчисления.51)y = 9x + 1/1 – xОтвет:Область определения функцииX₁ = 1y = 9x + 1/1 – x = 07. В задачах 61-70 найти полный дифференциал данной функции.61)z = arctg (y – x) + 1 / (y)^1/2 * (y)^1/3 * ln (1 – x) + sin(2x) + 1z = sin (2x) – arctan (x – y) + 1 + log (1 – x) / y^1/6Ответ: z = 1 – arctan (x – y) + log (1 – x) / y^1/6 + sin(2x)8. В задачах 71 – 80 найти неопределенные интегралы.71)∫ (x / (x + 2) – e^-3x+ sin 6x) dxОтвет: x – 2log (x + 2) – cos 6x / 6 + e^-3x / 3 + const9. В задачах 81-90 вычислить определенные интегралы.91)

---

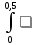arcsin³ x / (1 – x²)^1/2 dx 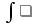arcsin³ (x) / (1 – x²)^1/2 dx = C + arcsin⁴ (x) / 4Пусть u = arcsin (x) => Тогда du = dx / (1 – x²)^1/2 , подставим du∫ u³ du∫ u³ du = u⁴ / 4 => arcsin⁴ (x) / 4Ответ: arcsin⁴ (x) / 4 + const10. В задачах 91-100 найти площадь фигуры, ограниченной линиямиy = x² – x; y = xОтвет: 4/3

---

Смотрите также файлы

• Задание на выполнение расчетнографической работы.pdf

• Прочитайте рассказы ответьте на вопросы и сформулируй правила безопасности в интернете из данного рассказа.docx

• Отношения между работником и работодателем регулируются Трудовым Кодексом рф.docx

• 1. 3 Предстерилизационная очистка инструментов.docx

• Программирование в ms excel. Применение технологии ole.doc