Построение графиков функций в MicrosoftExcelПроцесс построения графика функции состоит из двух этапов:

• 
  создание таблицы значений функции
  
• 
  непосредственного построения ее графика.
  

Для построения графика функции необходимо первоначально построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяют обычно с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала ее поведение на интервале табуляции. Вычисление и построение функций одной переменной в Excel

1. 
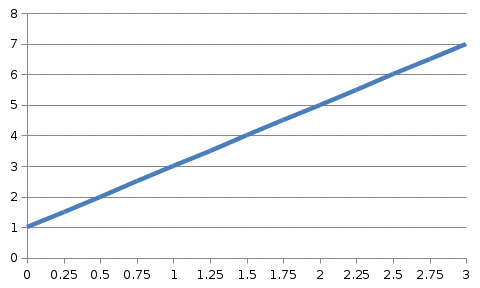
   Рассмотрим построение данной функции в Excel на примере уравнения
   

у=2х+1 в диапазоне : х[0; 3] с шагом х=0,25.1.1. Ввод данных. Для этого значения аргумента Х и функции У следует представить в таблице, первый столбец которой будет заполнен значениями Х , а второй – функцией У. 1.2. Построение графика функции. Выделите диаграмму и, используя вкладку Вставка  График, постройтеграфик функции у=2х+1 

2. 
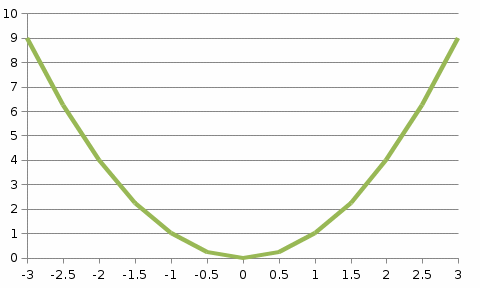
   Рассмотрим построение параболы вида:
   

у =х² в диапазоне х[–3; +3] с шагом х=0,5.

3. 
   Рассмотрим построение гиперболы 
   

y=1/x в диапазоне х[0,1: 10,1] с шагом х=0,5.

4. 
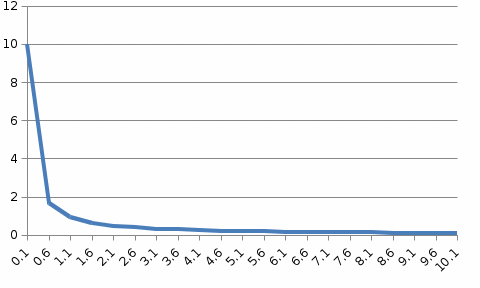
   Рассмотрим построение графиков функций y₁=x² и y₂=x³ на интервале [-3;3] с шагом 0,5.
   

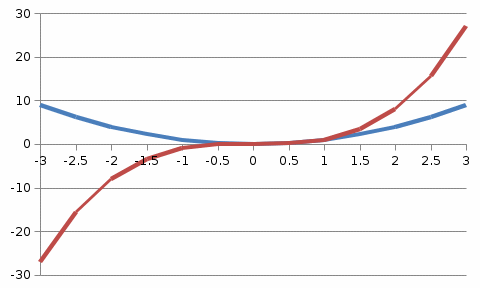
Задания для самостоятельного выполнения

1. 
   Построить график функции Зх+2у–4=0 в диапазоне х[–1; 3] с шагом =0,25.
   
2. 
   Построить график функции Зх–5у+15=0 в диапазоне х[–1; 3] с шагом =0,25.
   
3. 
   Построить график функции У=е2х в диапазоне х[0.1; 2] с шагом =0,2.
   
4. 
   Построить график функции У=2х в диапазоне х[–2; 2] с шагом =0,5.
   
5. 
   Построить график функции У=lnx в диапазоне х[0.5; 10] с шагом =0,5.
   
6. 
   Построить график функции Зх+2у–4=0 в диапазоне х[–1; 3] с шагом =0,25.
   
7. 
   Построить график функции y=2cos3x в диапазоне х[0.1; 1.8] с шагом =0,1.
   
8. 
   Построить график функции y=x² в диапазоне х[–3; 3] с шагом =0,25.
   
9. 
   Построить график функции y=1/2x в диапазоне х[0.1; 10] с шагом =0,25.
   
10. 
    Построить верхнюю часть параболы у²=х в диапазоне x[0; 4] с шагом =0,25.
    
11. 
    Построить гиперболу y =1/2х в диапазоне х [0,1; 5,1] с шагом =0,25
    
12. 
    Построить верхнюю полуокружность эллипса x⁴/4+у²=1 в диапазоне х [–2,25; 2,25] с шагом =0,25.
    
13. 
    Постройте параболу: у²=6х в диапазоне х [0; 4] с шагом =0,25. Найдите координаты фокуса и уравнение директрисы.
    
14. 
    Постройте параболу: х²=8у в диапазоне x [–2,25; 2,25] с шагом =0,25. Найдите координаты фокуса и уравнение директрисы.
    

---

Вычисление и построение сложных функций в ExcelВ качестве примера рассмотрим построение поверхностей второго порядка таких как: эллипсоид, гиперболоид, параболоид и т.п.1.Рассмотрим построение эллипсоида в Excel в соответствии с уравнением:Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х[–3; 3], у[–2; 2] с шагом =0,5 для обеих переменных.Решение данной задачи включает следующие этапы.1.1.Вначале необходимо разрешить уравнение относительно переменной z: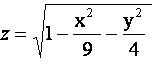1.2.Ввести значения переменных х (по вертикали), начиная с ячейки А2 и у (по горизонтали) , начиная с ячейки B1:

• 
  в ячейку А2 вводится первое значение аргумента (х = –3), затем в ячейку A3 вводится второе значение аргумента (х= –2,5) и, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента х (за правый нижний угол блока протягиваем до ячейки А14).
  
• 
  значения переменной увводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной (у = –2), в ячейку С1 вводится второе значение переменной ( у = –1,5) , а затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
  

1.3.Вычисление значений функции z. Для этого курсор необходимо поместить в ячейку В2 и вызвать Мастер функций. В появившемся диалоговом окне Мастер функций - шаг 1 из 2 слева в поле Категория выбираем Математические, в поле Функция выбираем функцию Корень и нажимаем кнопку ОК. В диалоговом окне Корень в рабочем поле вводим подкоренное выражение: 1 - $А2^2/9 - В$1^2/4. Обратите внимание, что символы $ предназначены для фиксации адреса столбца А - переменной хистроки 1 - переменной у. Нажимаем кнопку ОК и в ячейке В2 появляется « #ЧИСЛО!», так как при значениях х = –3 и у = –2 точек рассматриваемого эллипсоида не существует (рис 1.).1.4.Копирование значений функции из ячейки В2, для чего автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, а затем протягиванием вниз копируем в диапазоне ВЗ:J14

---

.

В результате должна быть получена таблица всех точек эллипсоида.

1.5.Построение диаграммы. Выделяем полученную таблицу (A1: J14), вызываем вкладку Вставка и в группе Диаграммы выбираем График  Все типы диаграмм окно Вставка диаграмм. В данном окне выбираем Поверхностьтип Проволочная поверхность и нажимаем ОК, в результате получаем поверхность эллипсоида. 

Далее,используясредства Работа с диаграммами , оформляем полученную поверхность. Например, вкладки Стенка и Основание диаграммы позволяют определить их цвета. Для этого выберите опцию Дополнительные параметры стенок и вид заливки, название диаграммы и т.п. Выполните данные действия самостоятельно.



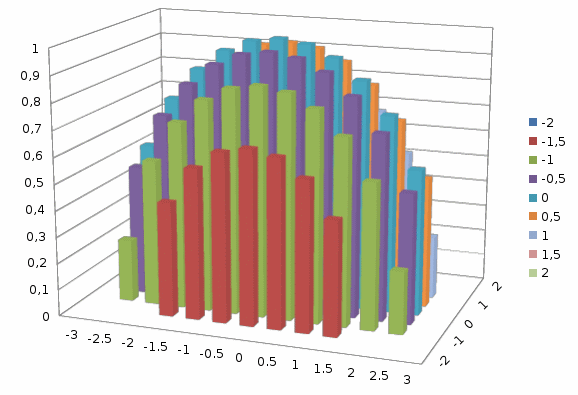
2. Рассмотрим построение гиперболоида следующего вида:



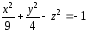
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах:

х[–3; 3], у[–2; 2] с шагом =0,5 для обеих переменных.

2.1.Вначале необходимо преобразовать уравнение относительно переменной Z:



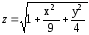
2.2.Введем значения переменной хв столбец А. Значения переменной увводим в строку 1.

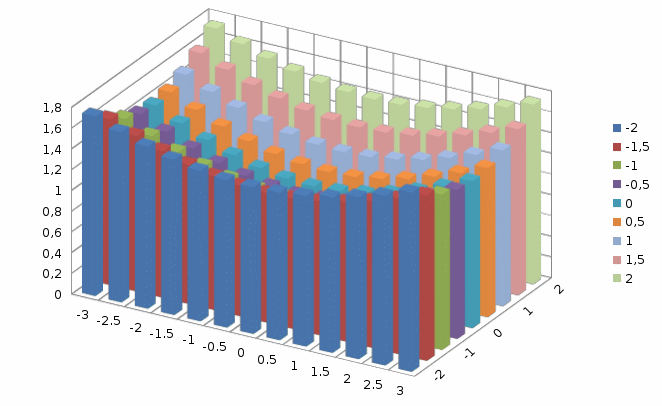
2.3.Вычисляем значения переменной Z. Для этого табличный курсор необходимо поместить в ячейку В2 , вызвать Мастер функций, в поле Категория выбрать Математические, в поле Функция выбираем функцию Корень и нажимаем кнопку ОК. В рабочее поле вводим подкоренное выражение: 1 + $А2^2/9 + В$1^2/4 инажимаем кнопку ОК. В ячейке В2 появляется 1,732051. Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего протягиванием вниз - в диапазоне ВЗ:J14.

В результате должна быть получена таблица точек гиперболоида



3. Рассмотрим построение графика функции с тремя условиями

Рассмотрим пример построения графика функции у при x[0; 1]:

---

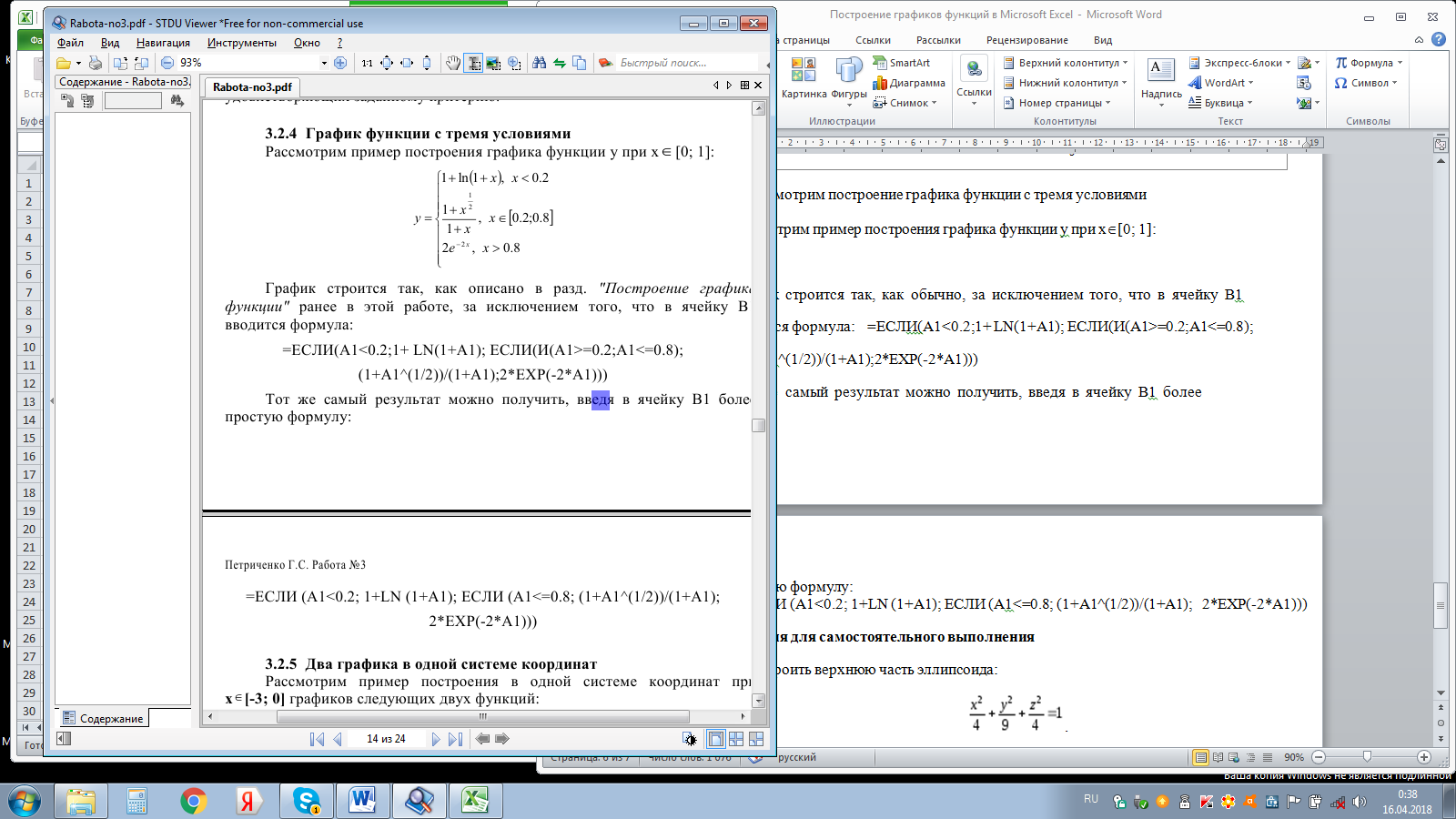
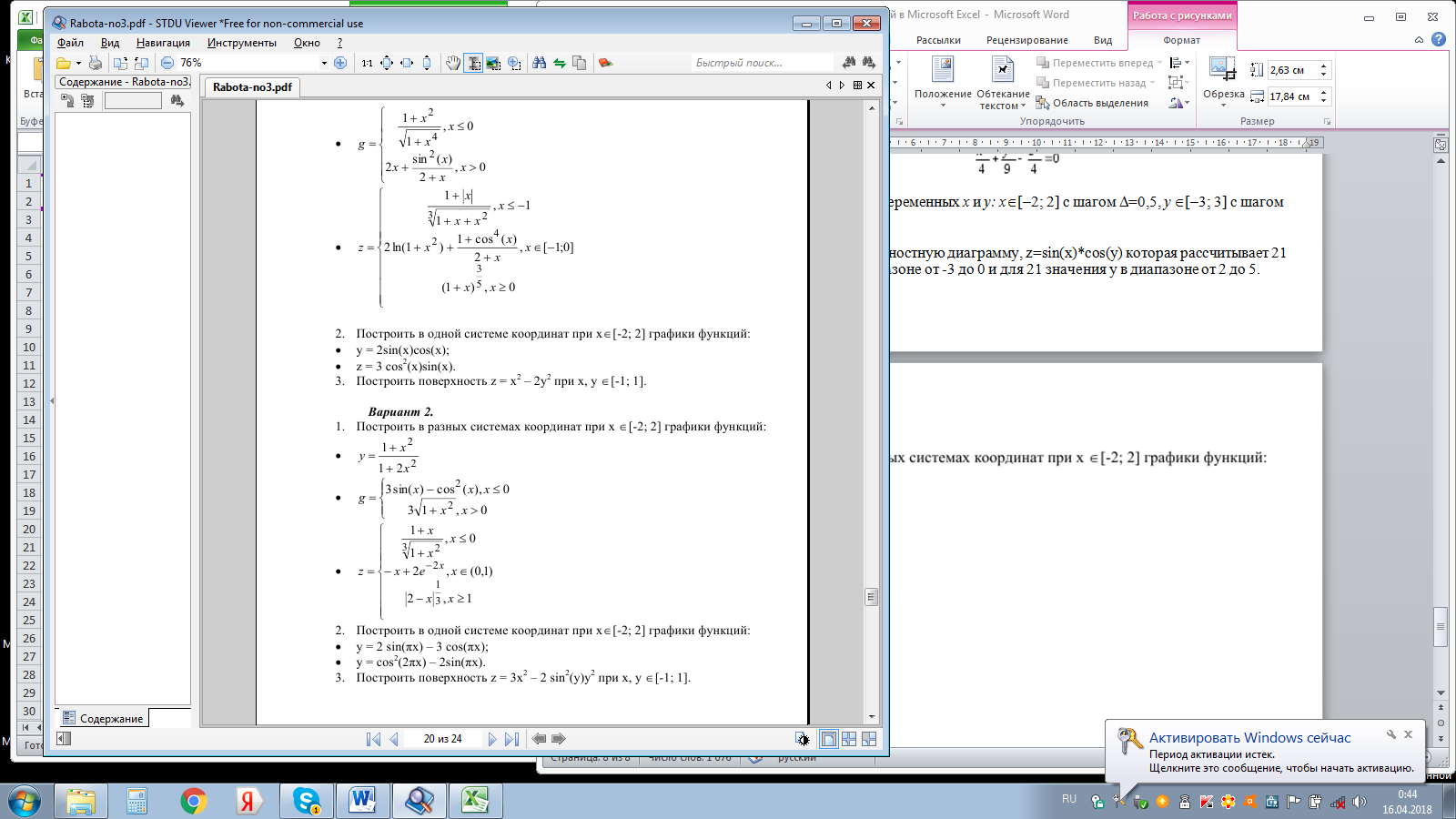
График строится так, как обычно, за исключением того, что в ячейку В1 вводится формула: =ЕСЛИ(А1<0.2;1+ LN(1+A1); ЕСЛИ(И(А1>=0.2;А1<=0.8); (1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1))) Тот же самый результат можно получить, введя в ячейку В1 более простую формулу: =ЕСЛИ (A1<0.2; 1+LN (1+A1); ЕСЛИ (А1<=0.8; (1+А1^(1/2))/(1+А1); 2*ЕХР(-2*А1)))Задания для самостоятельного выполнения1.Построить верхнюю часть эллипсоида: .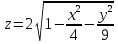Диапазоны изменения переменных х и у: х[–2; 2] с шагом =0,5, у[–3; 3] с шагом =1.2.Построить верхнюю часть однополостного гиперболоида: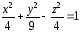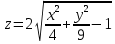Диапазоны изменения переменных х и у: х[–3; 3] с шагом =0,5, у[–4; 4] с шагом =1.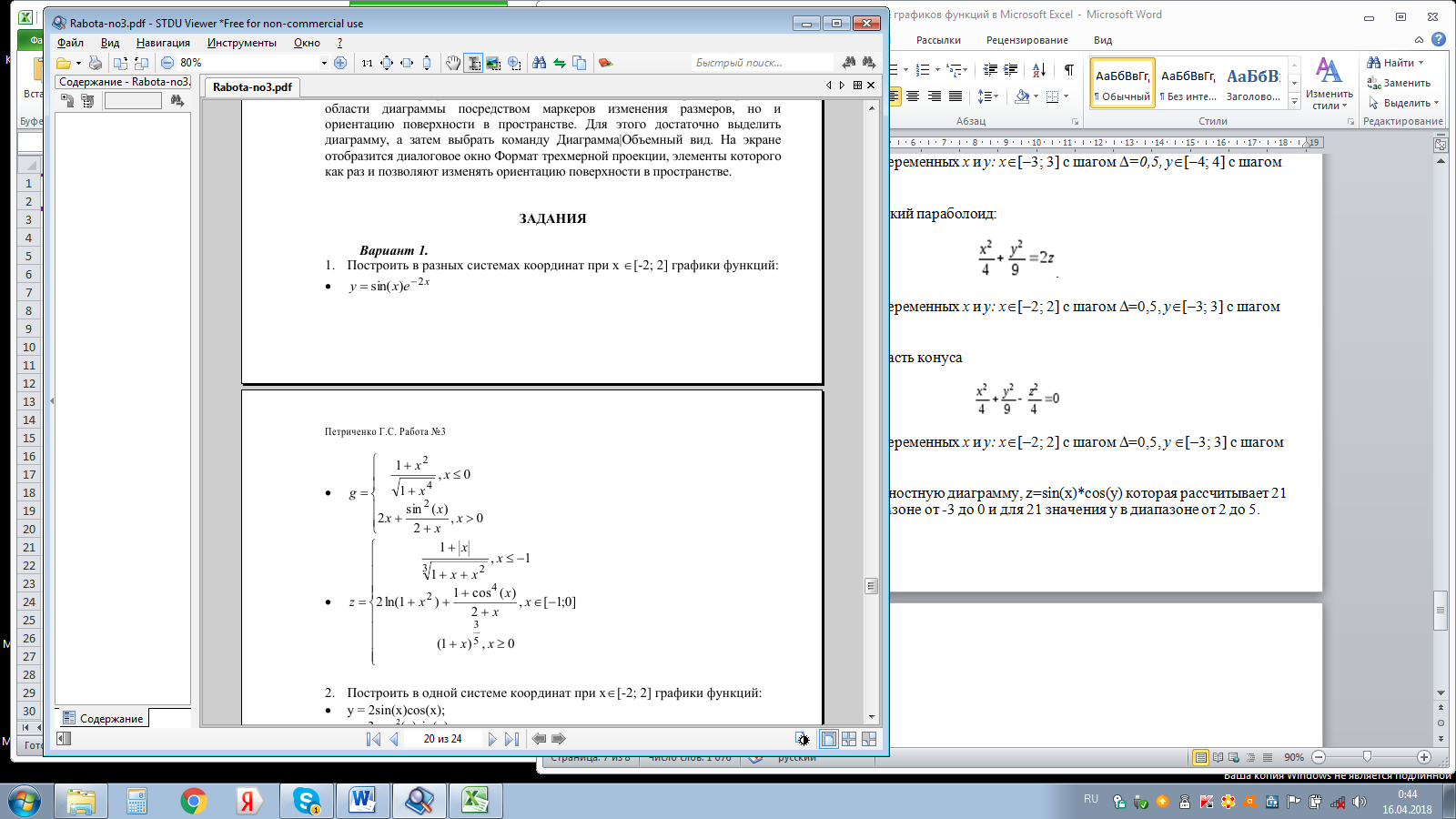3.Построить эллиптический параболоид: .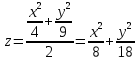Диапазоны изменения переменных х и у: х[–2; 2] с шагом =0,5, у[–3; 3] с шагом =1.4.Построить верхнюю часть конуса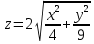Диапазоны изменения переменных х и у: х[–2; 2] с шагом =0,5, у [–3; 3] с шагом =1.

5. 
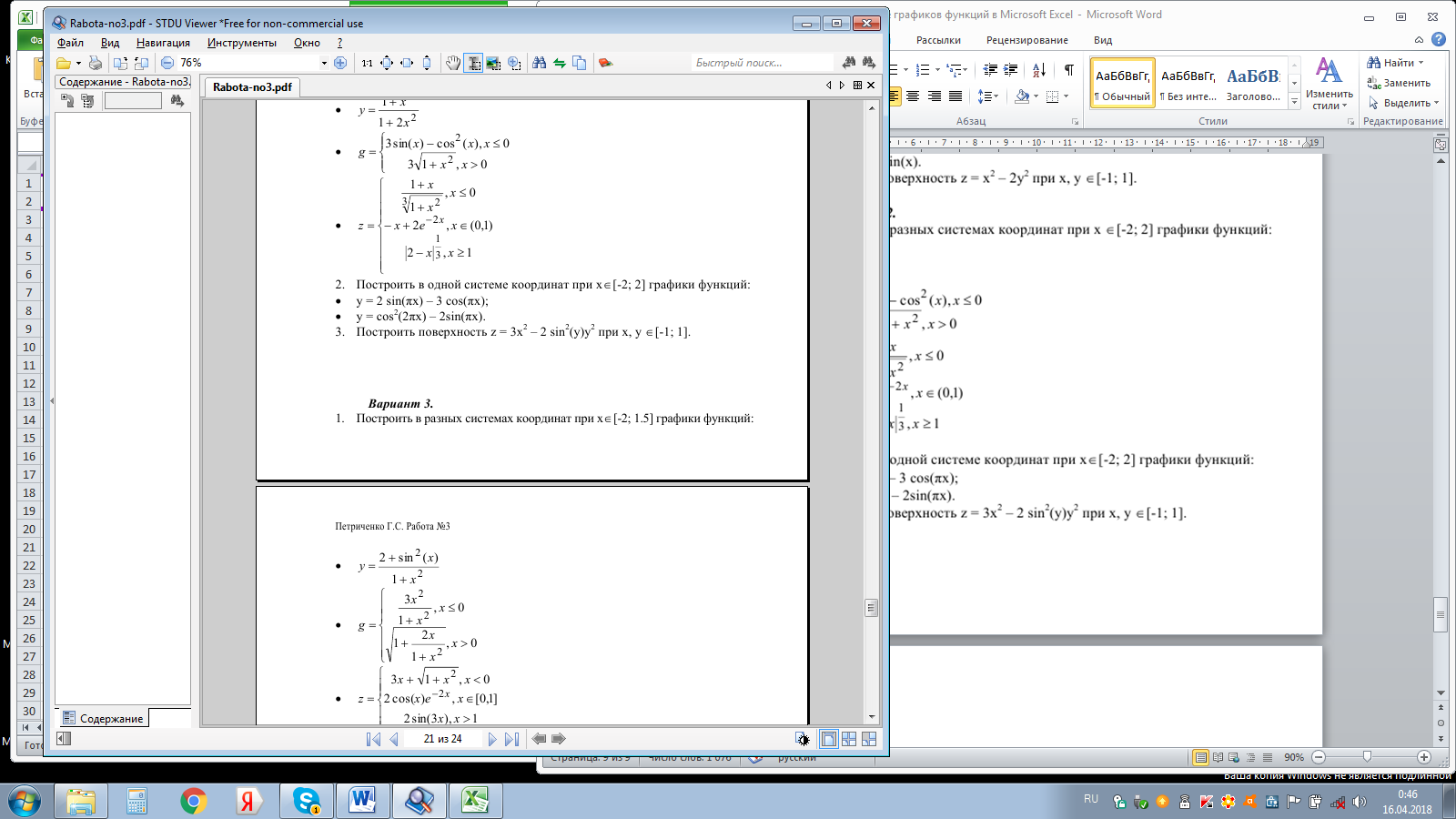
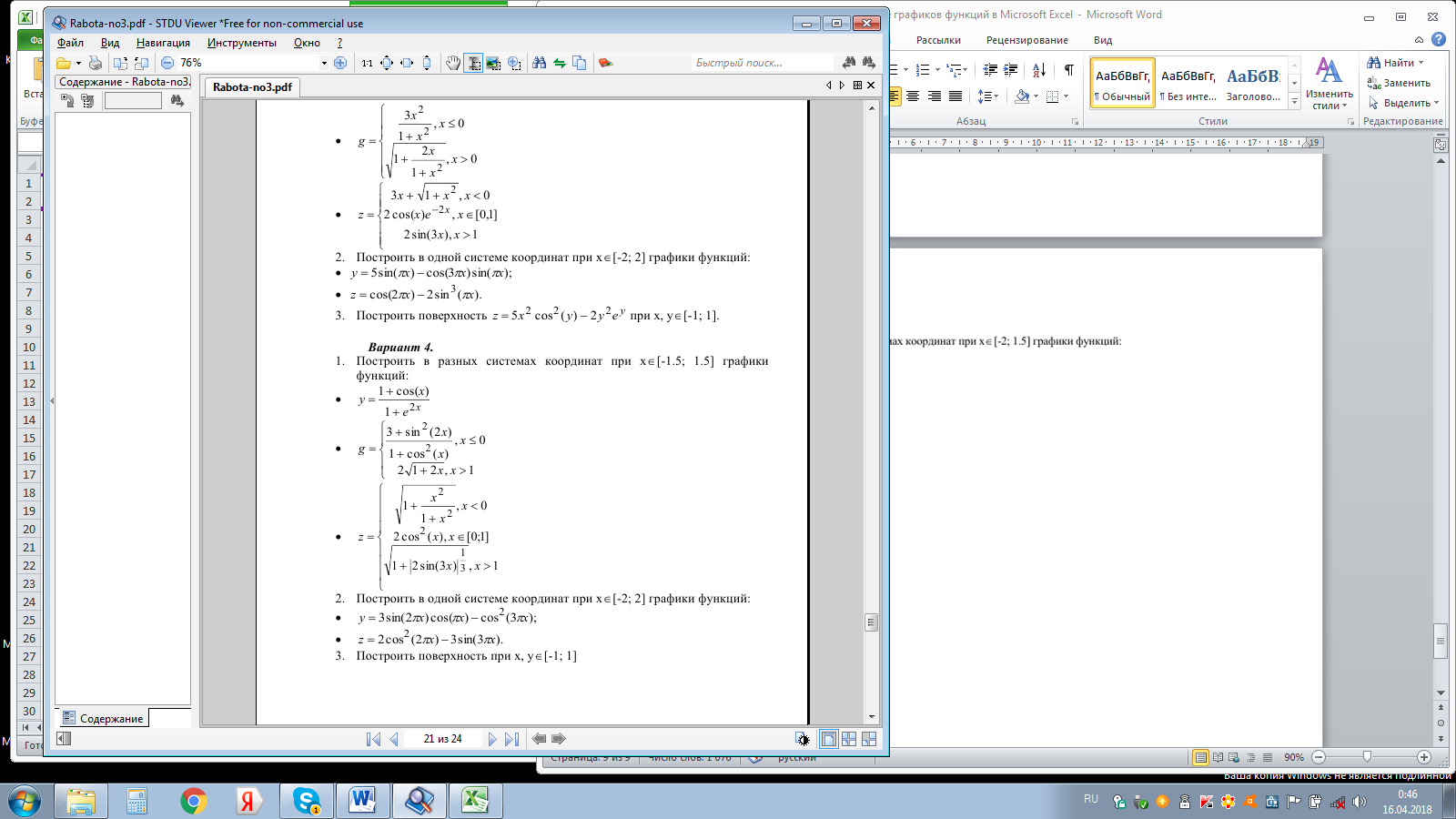
   Построить поверхностную диаграмму, z=sin(x)*cos(y) которая рассчитывает 21 значение x в диапазоне от -3 до 0 и для 21 значения y в диапазоне от 2 до 5.
   

---

Смотрите также файлы

• 1. Правильно ли сформулированы следующие вопросы. Найдите ошибки. Регулярно ли Вы питаетесь в ресторане быстрого обслуживания да, нет. Ответ.docx

• Рынок труда и его характерные особенности 1 Понятие и структура рынка труда 2 Особенности рынка труда и его функции.docx

• Викторина Ребусы Пословицы Простую воду 1 Что лучше всего пить в течение дня.pptx

• Хэл Страус Джерольд Крейсман я ненавижу тебя, только не бросай меня. Пограничные личности и как их понять.rtf

• воронежский государственный университет инженерных технологий.doc