МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИОрдена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования«Московский технический университет связи и информатики»Кафедра «Информатика»Лабораторная работа №4«Численное интегрирование»по дисциплине«Численные методы»Выполнил: студент гр. БИК2106 Михеева Е. В.Проверил: ст. преподаватель Юсков И. О.Москва, 2023 г.

1. 
   Индивидуальный вариант задания
   

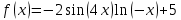– подынтегральная функцияa=−2.5, b=-1.5 – пределы интегрированияВычислить интеграл методом средних прямоугольников, написать программу для вычисления интеграла методом Симпсона.h₀=0,25 – начальный шаг интегрированияметоды интегрирования – средних прямоугольников, трапеций, Симпсона

2. 
   Метод средних прямоугольников
   

Правило РунгеЕго применяют для вычисления погрешности путём двойного просчёта интеграла с шагами 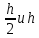, при этом погрешность вычисляется по формуле 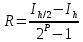.Полагают, что интеграл вычислен с точностью E, если 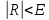; тогда 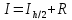, где I – уточнённое значение интеграла, P – порядок метода (для метода средних прямоугольников и трапеций – 2, для метода Симпсона – 4).Итак, перейдем к методу средних прямоугольников и оценим погрешность интегрирования методом двойного просчёта:

---

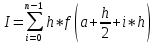
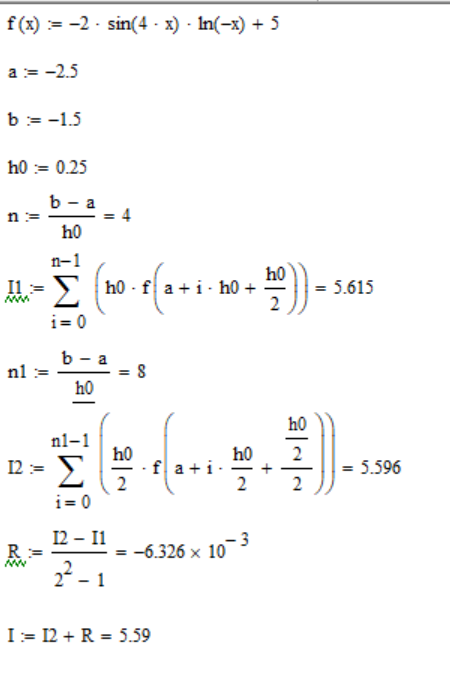
Из расчетов можем сделать вывод, что погрешность не превышает 10^-3, так как модуль R меньше, чем 10^-3.

3. 
   Метод Симпсона
   

Теперь вычисляю интеграл по формуле Симпсона используя программу, написанную мной на языке Python. По заданию надо вычислить точностями 10^-2, 10^-3, 10^-4.Программа представлена на следующем рисунке:import numpy as npimport math as mdef f(x):  return -2*m.sin(4*x)*m.log(-x)+5def Simpson(func,a,b,h):  n = (b-a)/h  f0 = func(a)  ev = 0  for i in range(1,int(n)):    f0 += 2*func(a+i*h) if ev else 4*func(a+i*h)    ev = not ev  f0 += func(b)  return f0*(h/3)def Solve(func,a,b,h,eps):  I1 = Simpson(func,a,b,h)  I2 = Simpson(func,a,b,h/2)  R = (I2-I1)/((2**4)-1)  print(R)  if np.abs(R) > eps:    return Solve(func,a,b,h/2,eps)  return I2+Rprint(Solve(f,-2.5,-1.5,0.25,10**-4))-0.00026182170223876255-1.4517635460660946e-05 5.590374499495849Исходя из результатов работы, можно сделать вывод что по формуле Симпсона интеграл вычисляется гораздо точнее, нежели по формуле прямоугольников. Чтобы увеличить точность расчётов, достаточно уменьшить шаг интегрирования h.

---

Смотрите также файлы

• Предпатологические состояния и заболевания при нерациональных занятиях физической культурой и спортом.ppt

• Театрализованная деятельность как средство развития креативной личности ребенка.docx

• Официальноделовой стиль язык документов.docx

• Висцеросенсорные зоны ЗахарьинаГеда понятие, клиническое значение.docx

• A в. ВельяминовЗернов.docx