Конспект урока

Информатика, 10 класс. Урок № 8.

Тема — Представление чисел в позиционных системах счисления

Урок посвящен теме «Представление чисел в позиционных системах счисления и переводу чисел из одной позиционной системы счисления в другую». В ходе урока школьники научатся различать позиционные и непозиционные системы счисления, узнают о развернутой форме числа. А также научатся переводить числа из одной системы счисления в другую.

Ключевые слова: Системы счисления, позиционная система счисления, непозиционная система счисления, базис системы счисления, схема Горнера, триада, тетрада, «компьютерные» системы счисления, «быстрый» перевод.

Учебник: Босова Л. Л, Босова А. Ю. Информатика 10 класс базовый уровень — БИНОМ Лаборатория знаний 2016 г.

Федерального центра информационных образовательных ресурсов:

http://fcior.edu.ru/

Мы постоянно оперируем числами, ежедневно, не слишком задумываясь о том, что они из себя изначально представляют. 

Счет появился тогда, когда человеку потребовалось информировать своих сородичей о количестве обнаруженных им предметов. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов свидетельствуют о том, что первоначально число предметов отображали равным количеством каких-либо значков:

точки, черточки. Такая система записи чисел называется единичной (унарной), т.к. любое число в ней образуется путем повторения одного знака, символизирующего единицу. Самым простым инструментом счета были пальцы на руках человека

Унарная система — не самый удобный способ записи чисел: при написании больших чисел получается очень длинная запись. С течением времени возникли иные, более удобные и экономичные системы: Вавилонская, Египетская, Славянская, Римская и другие. Рассмотренные записи чисел называются системами счисления.

Система счисления — это способ записи чисел.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемые цифрами.

Алфавит системы счисления 

---

—это используемый в ней набор цифр.

Основание системы счисления —это количество цифр в алфавите (мощность алфавита).

Различают непозиционные и позиционные системы счисления.

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения этой цифры в числе.

Примером непозиционной системы, которая сохранилась до наших дней, может служить система Древнего Рима.



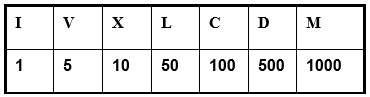
Римская система счисления. В качестве цифр использовались большие латинские буквы. А остальные числа записываются комбинациями этих знаков. Число формировалось из цифр, а также с помощью групп: Группа 1-го вида — несколько одинаковых подряд идущих цифр: XX = 20 (не более трёх одинаковых цифр); Группа 2-го вида — разность значений двух цифр, если слева стоит меньшая: СМ = 1000 – 100 = 900 (может стоять только одна цифра). Величина числа суммируется из значений цифр и групп 1-го или 2-го вида.

Позиционные системы счисления.

Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (места, позиции) в записи числа. Основное достоинство любой позиционной системы счисления — возможность записи произвольного числа ограниченным количеством символов. Пример этой системы — привычная нам десятичная система счисления. Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q>1, называемым основанием системы счисления. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр. В q-ичной системе счисления q единиц какого-либо разряда образуют единицу следующего разряда. Последовательность чисел, каждое из которых задает «вес» соответствующего разряда, называется базисом позиционной системы счисления. Представление числа в виде суммы разрядных слагаемых называется развёрнутой формой записи числа в системе счисления с основанием q. Свёрнутой формой представления числа называется его запись в виде:

Свернутой формой записи числа мы пользуемся в повседневной жизни. Развёрнутая форма записи чисел также всем хорошо известна. Ещё в начальной школе дети учат записывать числа в виде суммы разрядных слагаемых. Если представить разряды в виде степеней основания, то получим:

---

Иногда бывает полезно преобразовывать развернутую форму записи числа так, чтобы избежать возведения основания в степень. Такую формулу представления числа называют схемой Горнера.



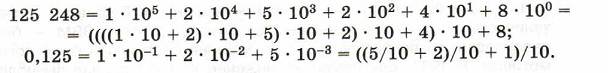
В наши дни большой практический интерес представляют двоичная, троичная, восьмеричная и шестнадцатеричная системы счисления. Двоичная система счисления — самая важная для компьютеров. В двоичной системе счисления основание — 2, а алфавит состоит из двух цифр 0 и 1.

Перевод числа, записанного в системе счисления с основанием q, в десятичную систему счисления основан на использовании развёрнутой формы записи чисел.

Алгоритм перевода в 10-ю систему счисления:

1. 
   Записать развёрнутую форму числа.
   
2. 
   Представить все числа, фигурирующие в развёрнутой форме, в 10-й системе счисления.
   
3. 
   Вычислить значение полученного выражения.
   

Перевод в десятичную систему счисления целых двоичных чисел будет значительно проще, если вспомнить и использовать уже знакомую вам таблицу степеней двойки.



Рассмотрим пример:

Для перевода двоичного числа в десятичную систему счисления можно воспользоваться схемой Горнера.

1. 
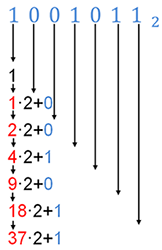
   Возьмем 1, соответствующую самому старшему разряду числа, и умножим её на 2.
   
2. 
   Прибавим следующую цифру.
   
3. 
   Умножим результат на 2.
   
4. 
   Прибавим следующую цифру.
   
5. 
   Умножим результат на 2.
   
6. 
   Прибавим следующую цифру.
   
7. 
   Умножим результат на 2.
   

Рассмотрим несколько примеров решения задач.

Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления. Решение: поскольку в записи числа 212_q есть цифра 2, то можно сказать, что q>2. Представим число 212_q в развёрнутой форме и приравняем к 57.

Решим уравнение: это квадратное уравнение, его корни Х₁ = –5,5; Х₂ = 5. Так как основание системы счисления должно быть натуральным числом, то q = 5

---

Перевод целого десятичного числа в систему счисления с оcнованием q

Для перевода целого десятичного числа в систему счисления с основанием q следует:

1. 
   Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю.
   
2. 
   Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления.
   
3. 
   Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
   

Для перевода целого десятичного числа в двоичную систему счисления можно воспользоваться таблицей степеней двойки. Рассмотрим пример: переведем число 529 в двоичную систему счисления.

Представим число в виде суммы степеней двойки, для этого:

— возьмем максимально возможное значение, не превышающее исходное число (512 < 529);

— найдем разность между исходным числом и этим значением (17);

— выпишем степень двойки, не превышающее эту разность и т. д. Когда исходное число было представлено в виде суммы, мы построили его двоичное представление, записав 1 в разрядах, соответствующих слагаемых, вошедшим в сумму, и 0 – во всех остальных разрядах.

529₁₀ = 512 + 17 = 512 + 16 +1 = 2⁹ + 2^{4 +} 2⁰ = 1000010001₂

Перевод десятичной дроби в систему счисления с основанием q

Для перевода конечной десятичной дроби в систему счисления с основанием q следует:

1. 
   Последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа.
   
2. 
   Полученные целые части (цифры числа) привести в соответствие алфавиту новой системы счисления.
   
3. 
   Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
   

При необходимости перевод целого числа 

---

А из системы счисления с основанием p в систему счисления с основанием q можно свести к хорошо знакомым действиям в десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления.



Быстрый перевод чисел в компьютерных системах счисления

Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q=2ⁿ) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод. Для этого:

1. 
   Данное двоичное число надо разбить справа налево на группы по n цифр в каждой.
   
2. 
   Если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов.
   
3. 
   Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2ⁿ.
   

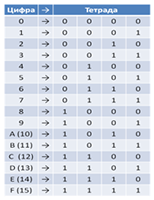
Рассмотрим перевод целых чисел между двоичной и 16-ной системами счисления

 

Рассмотрим перевод дробной части между двоичной и восьмеричной системами

Чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2ⁿ, достаточно:

двоичное число разбить слева направо на группы по n цифр в каждой; если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов; рассмотреть каждую группу как 

---

Смотрите также файлы

• Тестовые задания смк ргутиС.pdf

• Сборник статей, вопросов и ответов Содержание кратко о месяце рамадан о достоинствах месяца Рамадан и поста в нем 2.pdf

• Название тренинга Тут можно вставить крылатое выражение или афоризм.docx

• Б) составить словарь ключевых понятий Исихазм (безмолвие) древняя традиция духовной практики, составляющая основу православного аскетизма. Философия всеединства.docx

• Теоретические основы оценки финансового состояния предприятия.docx