Файл: Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 94
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
7. Расчет нормированного к амплитуде переносчика спектра модулированного сигнала и его начальной ширины спектра. Построение в масштабе графика нормированного спектра сигнала дискретной модуляции
Для передачи ИКМ сигнала по непрерывному каналу связи используется гармонический переносчик.
Сигнал ДАМ представляется в виде (формула (24)):
 (24)
(24)Разложение по гармоническим составляющим для такого сигнала имеет вид:
 (25),
(25),где mам=/2.
 =1,2*104.
=1,2*104.Ширина спектра сигнала ДАМ (на рисунке 15 показана пунктиром) определяется по формуле (26):
Спектр сигнала ДОФМ представлен на рисунке 15.
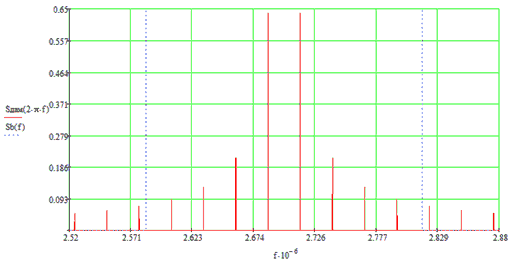
Рисунок 15 - Спектр ДАМ сигнала
8. Расчет мощности и амплитуды модулированного сигнала, дисперсии (мощности) аддитивной помехи в полосе частот сигнала, пропускную способность НКС
Рассматриваем НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум.
Мощность, приходящаяся в среднем на один двоичный символ определяется по формуле (27):
где Pш - мощность аддитивной помехи в полосе частот сигнала и рассчитывается по формуле (28):
G0 - постоянная энергетического спектра шума НКС. По условию G0 = 0.0002 Вт
с;
h02 - отношение сигнал/шум по мощности на входе детектора. По условию h02= 15.
Амплитуду модулированного сигнала находим по формуле (29):
Пропускная способность канала рассчитывается по формуле (30):
С = 0.2056*106*2.77=570221
Функции плотности вероятности аддитивной (ФПВ) гауссовой помехи определяется выражением (31):
 (31)
(31)ФПВ аддитивной гауссовой помехи изображена на рисунке 16.
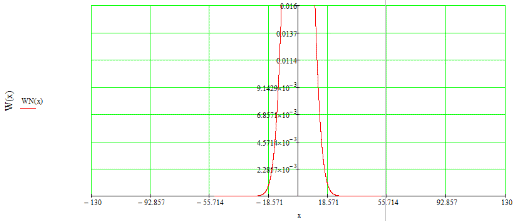
Рисунок 16 - ФПВ аддитивной гауссовой помехи
ФПВ огибающей помехи определяется по закону Рэлея (32):
 (32)
(32)ФПВ огибающей помехи представлена на рисунке 17.
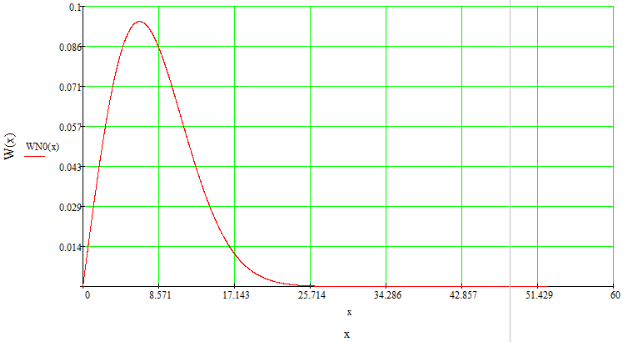
Рисунок 17 - ФПВ огибающей помехи
ФПВ суммы сигнала и помехи определяется выражением (33):
 (33)
(33)ФПВ суммы сигнала и помехи представлена на рисунке 18.
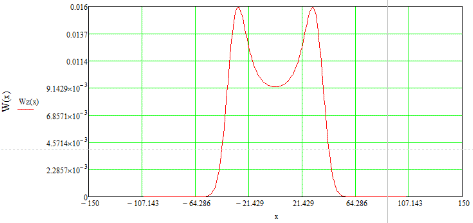
Рисунок 18 - ФПВ суммы сигнала и помехи
ФПВ огибающей суммы определяется распределением Райса (34):
 (34),
(34),где I0 (x) - модифицированная функция Бесселя нулевого порядка от мнимого аргумента.
ФПВ огибающей суммы представлена на рисунке 19.
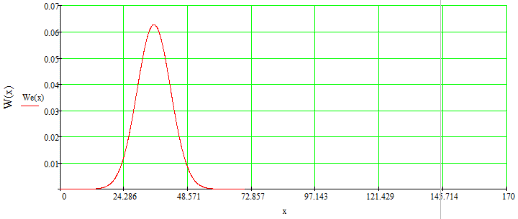
Рисунок 19 - ФПВ огибающей суммы
9. Расчет средней вероятности ошибки в двоичном ДКС, скорости передачи информации по двоичному симметричному ДКС
, показателя эффективности передачи сигнала дискретной модуляции по НКС с учетом заданного вида приема (детектирования) сигнала дискретной модуляции
Построение схемы приемника сигналов дискретной модуляции.
Схема приемника представлена на рисунке 20.
Р

исунок 20 - Схема приемника сигналов дискретной модуляции
Под действием помех в канале связи РУ может выносить неправильные решения, т.е. могут возникать ошибки первого и второго рода, т.е. p (0|1) и p (1|0). Помехоустойчивость системы характеризуется средней вероятностью ошибки:
Pошср = P (0) P (1|0) + P (1) P (0|1) = Pош (35)
При некогерентном приеме для системы с ДАМ имеем:
Pош=0.5е-0.5 h2 (36)
Pош=2.765*10-4
Энтропия ошибочных решений определяется по формуле (37):
Hош = - Pош log 2 Pош - (1-Pош) log 2 (1-Pош)) (37)
Hош = 0.0037
Скорость передачи информации по дискретному каналу связи определяют как взаимное количество информации, передаваемой по ДКС, в единицу времени по формуле (38):
R = log 2 L (1-Hош) fд (38)
R = 3*0.9963*8000=23911,975
Эффективность системы передачи определяется по формуле (39):
Э = R / C (39)
где C=570221 - пропускная способность канала. Э = 0.042
10. Расчет распределения вероятностей дискретного сигнала на выходе декодера, скорости передачи информации по L-ичного ДКС, относительных потерь в скорости передачи информации по L-ичного ДКС. Построение в масштабе графика закона распределения вероятностей отклика декодера
Рассмотрим отклик декодера ПРУ как случайный дискретный сигнал на выходе L-ичного ДКС.
Вероятности восстановленных уровней передаваемого сообщения рассчитываются по формуле (40):
где Pm - распределение вероятностей отклика квантователя.
Сравнительный график, указанных распределений вероятностей (восстановленных уровней и отклика квантователя) представлен на рисунке 21.
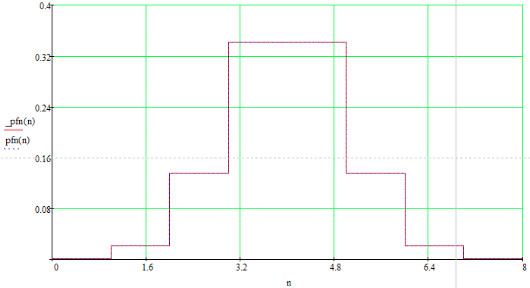
Рисунок 21 - Распределение вероятностей сигнала на выходе декодера
Из графика видно, что эти распределения практически совпадают.
Скорость передачи информации по L-ичному ДКС определяется следующим выражением (41):
где Hy`=16835;
Hx - энтропия восстановленного L-ичного сообщения определяется по формуле (42):
 (42)
(42)Hx=2.107;
Отсюда: RL=16771.501
Зная производительность L-ичного источника и скорость передаваемой по ДКС информации, находим величину относительных потерь в скорости по формуле (43):
R = 1 - RL / Hy` (43)
R = 1- (16771.501/16835) =0.0038
11. Расчет дисперсии случайных импульсов шума передачи на выходе интерполятора ЦАП, средней квадратической погрешности шума передачи (СКПП), суммарной начальной СКП восстановления непрерывного сообщения (СКПП), относительной СКП (ОСКП)
Предположим, что ФНЧ на выходе ЦАП приемника идеальный с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения.
Дисперсия случайных импульсов шума передачи определяется выражением (44):
 (44)
(44)где pn - распределение вероятностей отклика квантователя, pnm - условное распределение вероятностей в L-ичном ДКС, определяемое выражением (45):
где dnm - кодовое расстояние между n-й и m-й кодовыми комбинациями.
Вычисления дают результат: п2 = 0.00929.
Спектр плотности мощности шума передачи рассчитывается по формуле (46):
 (46)
(46)При условии, что ФНЧ на выходе ЦАП обладает полосой пропускания 0, средняя квадратическая погрешность шума передачи (СКПП) находится по формуле (47):
 (47)
(47)Вычисления дают результат:
Суммарная начальная СКП восстановления непрерывного сообщения (ССКП) определяется выражением (48):
где
= 0.95 - СКП фильтрации
Вычисления дают результат:
Относительная СКП (ОСКП) определяется по формуле (49):
 (49).
(49). =1,097 /2.5 = 0.439.
Будем, считать, что сообщение, переданное по каналу связи, безошибочно принято приёмником и декодировано, т.е. сигнал на выходе квантователя совпадает с сигналом на выходе декодера.
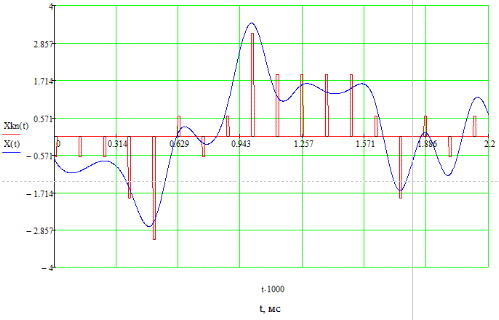
Рисунок 22 - Сигнал на выходе декодера
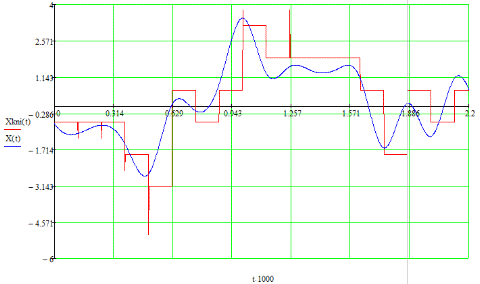
Рисунок 23 - Сигнал на выходе интерполятора ЦАП
Качественный вид сигнала на выходе системы электросвязи представлен на следующем рисунке 24 (красная линия).
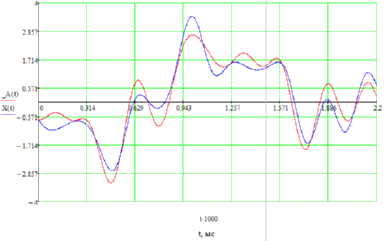
Рисунок 24 - Восстановленное сообщение на выходе системы электросвязи
На данном, а также на двух предыдущих рисунках, синей линией изображен исходный сигнал, поступивший на вход системы электросвязи. Как видно из рисунка, сигнал на выходе системы хорошо повторяет сигнал на ее входе. В интервале времени от t=1.57 до t=1.8 мс сигнал на выходе лучше всего повторяет исходный.