Файл: Все твердые тела, в которых слагающие их частицы (атомы, ионы, молекулы) расположены закономерно, образуя упорядоченную трехмернопериодическую структуру в виде пространственной решетки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 24
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Кристаллическим веществом являются все твердые тела, в которых слагающие их частицы (атомы, ионы, молекулы) расположены закономерно, образуя упорядоченную трехмерно-периодическую структуру в виде пространственной решетки. Пространственная решетка представляет собой бесконечную закономерную систему узлов (точек), характеризующих общую для всех кристаллов геометрическую особенность их строения.
Основными свойствами кристаллов являются их однородность, анизотропность, способность самоограняться и симметричность.
Однородным обычно называют тело, которое обнаруживает одинаковые свойства во всех своих частях. Кристаллическое тело однородно, т. к. различные участки его имеют одинаковое строение, т. е. одинаковую ориентировку слагающих частиц, принадлежащих одной и той же пространственной решётке. Однородность кристалла следует отличать от однородности жидкости или газа, которая имеет статистический характер.
Анизотропным называется такое однородное тело, которое обладает неодинаковыми свойствами по непараллельным направлениям. Кристаллическое тело анизотропно, т. к. строение пространственной решётки, а значит и самого кристалла, в общем случае неодинаково по непараллельным направлениям. По параллельным же направлениям частицы слагающие кристалл, как и узлы его пространственной решётки, расположены строго одинаковым образом, поэтому и свойства кристалла по таким направлениям должны быть одними и теми же.
-
К элементам симметрии кристалла относятся ось симметрии, плоскость симметрии, центр симметрии. В современной кристаллографиче-ской литературе приняты следующие символы для их обозначения: ось симметрии - L, плоскость симметрии - Р, центр симметрии - С. -
ТЕОРЕМА 1. Линия пересечения двух плоскостей симметрии является осью симметрии, причем угол поворота вокруг этой оси вдвое больше угла между плоскостями.
ТЕОРЕМА 2. Точка пересечения четной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии (центр инверсии)
Зная эту теорему, можно сделать некоторые важные практические выводы: 1)если при исследовании кристаллического многогранника найдены два элемента симметрии из трех (ось симметрии четного порядка, перпендикулярная к ней плоскость, центр инверсий), то обязательно нужно найти недостающий элемент симметрии;2) при наличии центра инверсии количество четных осей симметрии равно числу плоскостей симметрии.
ТЕОРЕМА 3. Если есть ось симметрии порядка «n» и перпендикулярно этой оси проходит ось второго порядка, то всего содержится «n» осей 2го порядка, перпендикулярных оси n-го порядка. Например, в гексагональной дипирамиде, (рис 4.9) шесть осей второго порядка проходят через вершины и середины сторон шестиугольника дипирамиды, а главная ось фигуры L6 перпендикулярна всем осям второго порядка, и всего есть 6L2 перпендикулярных L6.
ТЕОРЕМА 4. Если есть ось симметрии n го порядка, и вдоль нее проходит плоскость симметрии, то всего через эту ось будет проходить «n» таких плоскостей.
В самом деле, на данном рисунке видно, вдоль оси L6 пересекается шесть плоскостей симметрии.
ТЕОРЕМА 5. (выделена впервые русским математиком Леонардом Эйлером, и носит его имя)
Через точку пересечения двух осей симметрии проходит третья ось симметрии. Из рис.4.9 видно, что через точку пересечения двух осей второго порядка действительно проходит третья ось симметрии.
-
Формулировка закона: углы между соответствующими гранями кристалла одного и того же вещества постоянны, грани при росте кристалла передвигаются параллельно самим себе.
Самым первым методом исследования внешней морфологии кристаллов. был метод гониометрии, основанный на законе постоянства углов между соответствующими гранями.
-
В кристаллах высшей категории (кубическая сингония), благодаря их высокой симметрии, единичных направлений нет – любому направлению найдутся симметрично-равные направления. В кристаллах средней категории возможно только одно единичное направление, совпадающее с единственной осью симметрии высшего порядка. Все другие направления этой осью симметрии будут размножаться. Заметим сразу, что это дает дополнительный критерий для обнаружения инверсионной оси симметрии четвертого порядка. Если найденная ось L2является единичным направлением, и других единичных направлений в фигуре нет, то это ось Li4.
Для низшей категории единичных направлений больше одного, но в разных сингониях их разное количество. Кристаллы ромбической сингонии имеют три взаимно перпендикулярных оси симметрии второго порядка – простые или инверсионные (перпендикуляры к плоскостям симметрии). С этими осями совпадают три единичных направления. Действительно, каждое из этих направлений двумя оставшимися перпендикулярными к нему осями симметрии не размножается – происходит лишь совмещение противоположных концов направления при повороте на 180
○ вокруг L2 или при отражении в плоскостиm. Любые другие направления, кроме этих трех, осями симметрии второго порядка или плоскостями симметрии размножаются (удваиваются). В кристаллах моноклинной сингонии имеется только одна ось второго порядка – простая или инверсионная. Направление, совпадающее с этой осью, является единичным и не размножается, так как других элементов симметрии (кроме, может быть, центра инверсии) нет. Кроме того, не размножаются и все направления, лежащие в плоскости, перпендикулярной L2 или Li2 (т.е. в плоскости m). Итак, в кристаллах моноклинной сингонии имеется множество единичных направлений (различающихся между собой!), но не все направления единичны. В кристаллах триклинной сингонии единичны все направления (и все они между собой различаются), поскольку нет элементов симметрии, которые бы их размножали. Если есть центр инверсии, то он лишь совмещает разные концы каждого направления.
-
А. Виды симметрии кристаллов, обладающих единичными направлениями. Относящиеся сюда кристаллические многогранники имеют по меньшей мере одно единичное направление. Примем его за исходное. Будем последовательно присоединять к нему элементы симметриитак, чтобы оно оставалось единичным.
1) Единичное направление совпадает с единственной осью симметрии Ln. L1, L2, L3, L4, L6 – примитивные виды симметрии
2) К исходному единичному направлению прибавляется центр симметрии С. L1 +С=С, L2+С= L2РС, L3+С= L3С, L4+С= L4РС, L6+С= L6РС - цен-тральные виды симметрии.
3) К исходному единичному направлению прибавляется плоскость симметрии, идущая вдоль него. L1 +Р=Р, L2+Р= L22Р, L3+Р= L33Р, L4+Р= L44Р, L6+Р= L66Р - планальные виды симметрии.
4) Перпендикулярно исходному единичному направлению присоединяется ось второго порядка. L1 + L2= L2, L2+L2= 3L2, L3+L2= L33L2, L4+L2= L44L2, L6+L2= L66L2 –аксиальные виды симметрии.
5) К исходному единичному направлению прибавляется центр симметрии С и плоскость симметрии, идущая вдоль него L1+С+Р=L2РС, L2+С+Р=3L23РС, L3+С+Р=L33L23РС, L4+С+Р=L44L25С, L6+С+Р= L66L27РС – планаксиальные виды симметрии.
6) Единичное направление совпадает с инверсионной осью симметрииL
in Li4, Li6 – инверсионно-примитивные виды симметрии.
7) К исходному единичному направлению прибавляется плоскость симметрии, идущая вдоль него. Li4+Р = Li42L22Р, Li6+Р = Li63L23Р – инверсиооно-планальные виды симметрии.
Б. Виды симметрии кристаллов, не обладающих единичными направлениями. Из каждого направления выводятся симметрично-равные ему.
1) Совокупность осей симметрии кубического тетраэдра принимаем за примитивный вид симметрии. 4L33L2
2) К исходной совокупности осей симметрии добавляем центр симметрии 4L33L2+С=4L33L23РС – центральный вид симметрии.
3) Вдоль осей третьего порядка проводим плоскости симметрии 4L33L2+Р=4L33L26Р – планальный вид симметрии.
4) Добавляем перпендикулярно осям третьего порядка оси второго порядка: 4L33L2+ L2=4L33L26L2 – аксиальный вид симметрии.
5) Добавляем перпендикулярно осям третьего порядка оси второго порядка и центр симметрии: 4L33L2+ L2+С =4L33L26L29РС – планаксиальный вид симметрии. В результате вывод получено тридцать два вида симметрии – тридцать две совокупности элементов симметрии, возможных для кристаллических многогранников.
7. Принцип стереографического проектирования следующий.
Из центра кристалла О произвольным радиусом описываем сферу проекции вокруг этого кристалла (рис.6.1). Разрезают сферу по экватору плоскостью Q, которая называется плоскостью проекции и образует при пересечении со сферой круг проекции, NS-ось проекции, S-южная точка зрения.
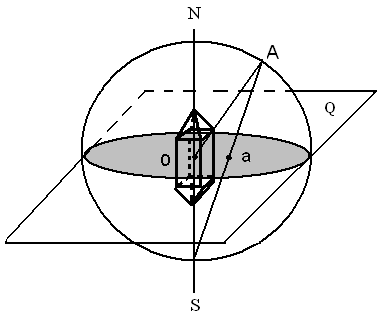
Рисунок 6.1 – Принцип стереографического проектирования
Чтобы спроектировать любое направление ОА на круг проекции, его продолжают до пересечения со сферой, а затем точку пересечения А мысленно соединяют с южной точки зрения S и наблюдают за тем, где луч зрения AS пересек круг проекции. Точка пересечения а и является проекцией направления ОА.
10.Наиболее часто в кристаллографии пользуются гномостереографическими проекциями. Они включают в себя достоинства, свойственные линейным и гномоническим проекциям, а именно: комплекс проектируется на плоскость, которая ограничена кругом проекций. Здесь так же, как и в предыдущих случаях, центр полярного комплекса совмещается с центром сферы(рис.1.16). Через центр сферы проводится плоскость проекции P, которая пересекает сферу по большому кругу. Это сечение называется основным кругом проекции.
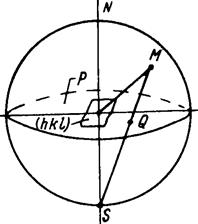
Рис.1.16. Гномостереографическая проекция.
Прямая, перпендикулярная к плоскости P и проходящая через центр О, пересекает сферу в двух точках N и S, которые называют полюсами проекций. При построении гномостереографической проекции плоскости (hkl) точку выхода ее нормали на сфере (точку M) соединяют с полюсом проекций, расположенным по другую сторону от плоскости Р. Точка пересечения прямой MS с плоскостью P (точка Q) и будет являться гномостереографической проекцией плоскости (hkl).
Легко видеть, что проекции всех плоскостей кристалла находятся в пределах большего круга. Таким образом, размеры проекции конечны и определяются радиусом сферы. В этом одно из достоинств гномостереографической проекции.
Построение гномостереографической проекции кристалла проводят, взяв только один из полюсов проекции, например S, и рассматривая нормали, направленные в одну сторону от плоскости проекций P. Тогда для каждой плоскости (hkl) получаем одну точку проекции (hkl), которую называют полюсом плоскости. Совокупность гномостереографических проекций плоскостей кристалла на большом круге проекций называется его полюсной фигурой (рис.1.17).
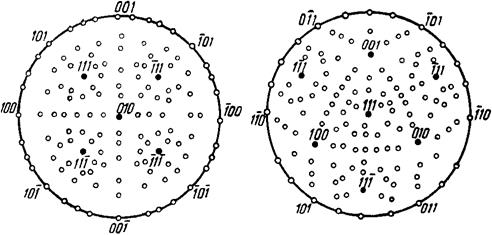
Рис. 1.17. Полюсные фигуры.
Вид полюсной фигуры зависит от симметрии кристалла, а также от его установки относительно плоскости проекций и прямой SN. При изменении установки кристалла все точки проекций на полюсной фигуре смещаются.
Плоскость или грань кристалла, перпендикулярная прямой SN, будет иметь проекцию в центре большого круга; все плоскости, параллельные прямой SN, спроектируются в виде точек на большом круге проекций. Все другие плоскости кристалла дадут точки проекций на остальной площади большего круга.
Рассмотрим, как будут располагаться на полюсной фигуре точки гномостереографической проекции какой-либо кристаллографической зоны (рис.1.18).
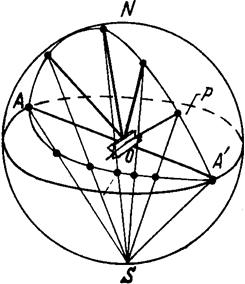
Рис. 1.18. Гномостереографическая проекция плоскостей одной зоны.
Для этого представим зону в виде полярного комплекса