Файл: Решение Так как насосы подключены параллельно, а расход жидкости необходимо удвоить, то имеет место равенство (30. 1).doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 17

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задача № 30

Поршневой насос простого действия с диаметром цилиндра , ходом поршня , числом двойных ходов в минуту и объемным кпд подает рабочую жидкость в систему гидропривода. При какой частоте вращения должен работать включенный параллельно шестеренный насос с начальным диаметром шестерен , шириной шестерен , числом зубьев и объемным кпд , чтобы количество подаваемой жидкости удвоилось?

Исходные данные:

; ; ; ; .

Решение:

Так как насосы подключены параллельно, а расход жидкости необходимо удвоить, то имеет место равенство:

. (30.1)

Подача поршневого насоса определяется по формуле:

, (30.2)

а подача шестеренного насоса по формуле [2, стр. 46]:

, (30.3)

где – частота вращения шестеренного насоса;

– радиус окружности головок;

– радиус начальной окружности;

– коэффициент, зависящий от степени перекрытия;

– основной шаг.

Радиус начальной окружности определим по формуле:

.

Коэффициент , зависящий от степени перекрытия, определим по формуле:

,

где – степень перекрытия.

Основной шаг определим по формуле:

. (30.4)

где – модуль;

– угол зацепления основной рейки.

Степень перекрытия определим по формуле:

,

где – радиус основной окружности;

– действительное расстояние между осями;

– угол зацепления передачи.

Модуль приближенно определим по формуле:

,

Вычислим модуль зубчатого зацепления:


,

полученное значение округляем до наименьшего стандартного значения и получаем .

Радиус основной окружности определим по формуле:

. (30.5)

Угол зацепления передачи определим по формуле:

, (30.6)

где – теоретическое расстояние между осями.

Теоретическое расстояние между осями определим по формуле:

, (30.7)

где – диаметр основной окружности.

Подставляя выражение (30.5) в (30.7) получаем теоретическое расстояние между осями

, (30.8)

полученное выражение (30.8) подставляем в (30.6) и получаем угол зацепления передачи :

.

Вычисляем угол зацепления передачи :

.

Радиус окружности головок определим по формуле:

,

где – диаметр окружности головок, который определим по формуле:

,

где
– коэффициент высоты зуба исходного контура;

– коэффициент профильного смещения;

– коэффициент уравнительного смещения.

Коэффициент высоты зуба исходного контура определим по формуле:

,

где – коэффициент высоты головки зуба шестерни;

– коэффициент воспринимаемого смещения.

Коэффициент профильного смещения определим по формуле:

,

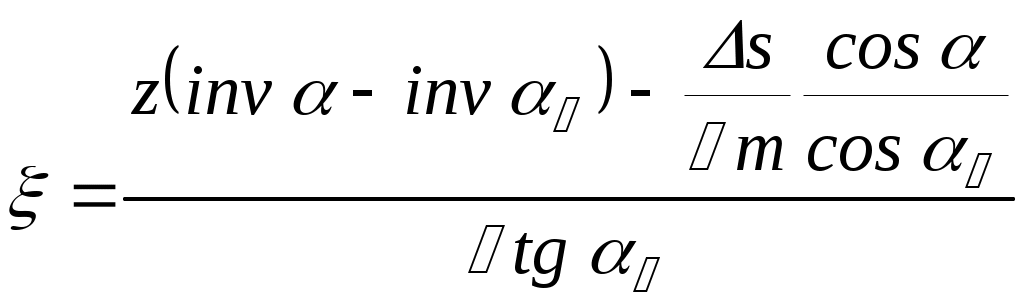где – боковой зазор по начальной окружности.

Коэффициент уравнительного смещения определим по формуле:

,

где – коэффициент суммарного смещения.

Коэффициент воспринимаемого смещения определим по формуле:

.

В нашем случае, когда и , коэффициент суммарного смещения равен:



Вычисляем коэффициент профильного смещения :

.

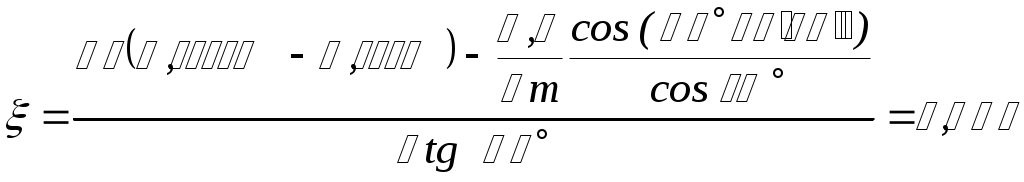Вычисляем коэффициент воспринимаемого смещения
:

.

Вычисляем коэффициент суммарного смещения :

.

Вычисляем коэффициент уравнительного смещения :

.

Вычисляем коэффициент высоты зуба исходного контура :

.

Вычисляем диаметр окружности головок :

.

Вычисляем радиус окружности головок :

.

Далее выражения (30.6) и (30.10) подставляем в (30.7) и получаем формулу для вычисления степени перекрытия :

.

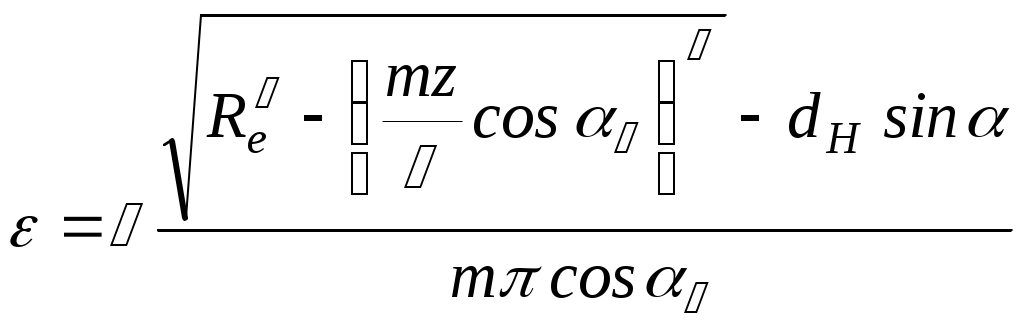Вычисляем степень перекрытия :

.

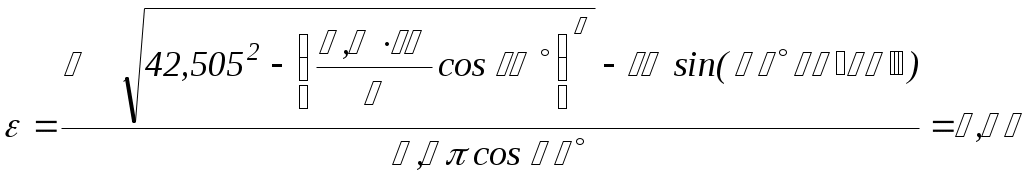Вычисляем коэффициент :

.

Вычисляем основной шаг :

.

Подставляя (30.2) и (30.3) в (30.1) выражая частоту вращения шестеренного насоса, получаем:

.

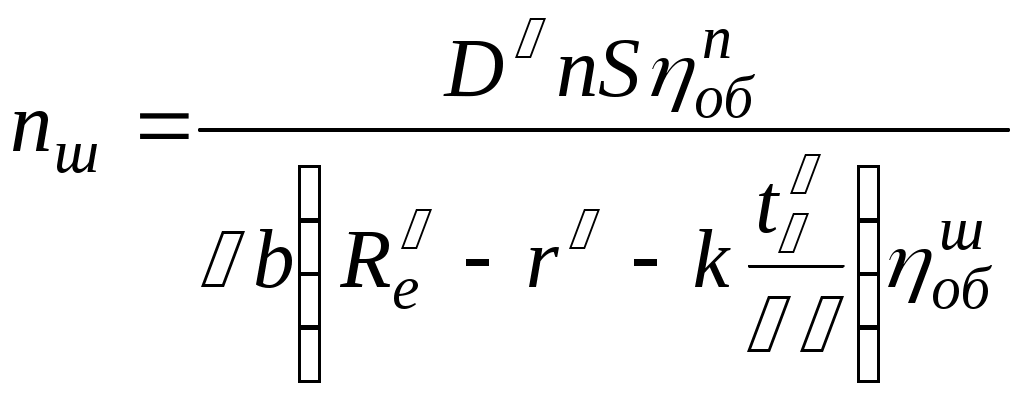по этой формуле и вычисляем частоту вращения

Смотрите также файлы