Министерство науки и высшего образования Российской Федерации

ФГАОУ ВО «Уральский федеральный университет имени

первого Президента России Б.Н.Ельцина»

Институт строительства и архитектуры

Кафедра строительной механики
Оценка: _____________________

Руководитель

проектирования: доц. Лялина Ф.Г.

Члена комиссии: проф. Чупин В.В.

доц. Черногубов Д.Е.

Дата защиты: __________________

ОТЧЕТ

о выполнении проекта по модулю

Строительная механика

по теме: метод перемещений в расчетах строительной механики

Студент: Хуснутдинова Д.Р.

Группа: СТ-370001(ПГС-1)

Екатеринбург

2019

Оглавление

1. Расчет статически неопределимой рамы методом перемещений. 3

1.1.Основные понятия 3

1.3. Основная система метода перемещений (ОСМП) и канонические уравнения 4

2.Расчет рам на устойчивость 9

2.1.Общие положения 9

2.2.Основные понятия 11

3.Свободные колебания системы с двумя и несколькими степенями свободы 13

1. Расчет статически неопределимой рамы методом перемещений.

   1. 
      Основные понятия
      

Р
асчет рам в ряде случаев упрощается, если за неизвестные принимать не силы, как в методе сил, а перемещения узлов рамы. Этот метод расчета называется методом перемещений (МП). Перемещения узлов в рамных конструкциях могут быть линейные и угловые. Так в раме на рис. 1, через ∆ обозначены линейные перемещения узлов, φ – угловые перемещения в среднем узле рамы. Надо иметь в виду, что в жестких узлах все стержни, сходящиеся в узле, поворачиваются на один и тот же угол. При этом в каждом узле углы поворота имеют свои значения, за исключением симметричных систем, где в симметричных узлах перемещения и углы поворота одинаковы.
Рис.1

2. 
   Определение степени кинематической неопределимости
   

Вводят следующие упрощения:

1. Продольные деформации стержней, вызванные продольными силами, не учитывают. Учет продольных деформаций производится только от действия температур;

2. Сдвиговыми деформациями, вызванными действием поперечных сил, пренебрегают;

3. Не учитывают сближение концов стержней рамы вследствие изгиба.

Перемещения узлов в рамах бывают двух типов – линейные и угловые,

поэтому общее число неизвестных перемещений К состоит из двух частей:

K = K1 + K2, где K1 – количество жестких бесшарнирных внеопорных узлов рамы;

К2 – число независимых линейных смещений узлов. В дальнейшем под К будем понимать степень кинематической неопределимости системы или число неизвестных перемещений по методу перемещений.

В отношении линейных перемещений рама подобна шарнирно-стержневой системе, поэтому для упрощения при определении K2 заданная система превращается в шарнирно-стержневую систему. Для этого вводятся шарниры во все жесткие и опорные узлы рамы, если в них заделки. После этого K2 определяется как степень свободы полученной системы: K = 2y − C,

где y – количество узлов, а С – количество стержней, включая опорные. При этом консоль не учитывается в качестве стержня.

Если при пользовании формулой K = 2y − C K получается со знаком

минус, то принимается K = 0.

3. 
   Основная система метода перемещений (ОСМП) и канонические уравнения
   

В отличие от метода сил, в котором основная система образуется путем удаления лишних связей, в методе перемещений основная система получается введением связей двух типов: защемлений и линейных связей – стерженьков. Защемления [ ] вводятся в жесткие узлы рамы и препятствуют их повороту. Линейные связи препятствуют линейным перемещениям узлов.

Структура вводимых связей диктуется формулой K = K₁ + K₂ : если K₁ = 3, то вводим три защемления, если K₂ = 2, то вводим две линейные связи. Рама, содержащая дополнительные связи и загруженная заданной нагрузкой, представляет собой основную систему метода перемещений (ОСМП).

Таким образом, основная система состоит из совокупности статически неопределимых балок с различными закреплениями на концах.

Канонические уравнения рассмотрим на примере рамы, приведенной

н
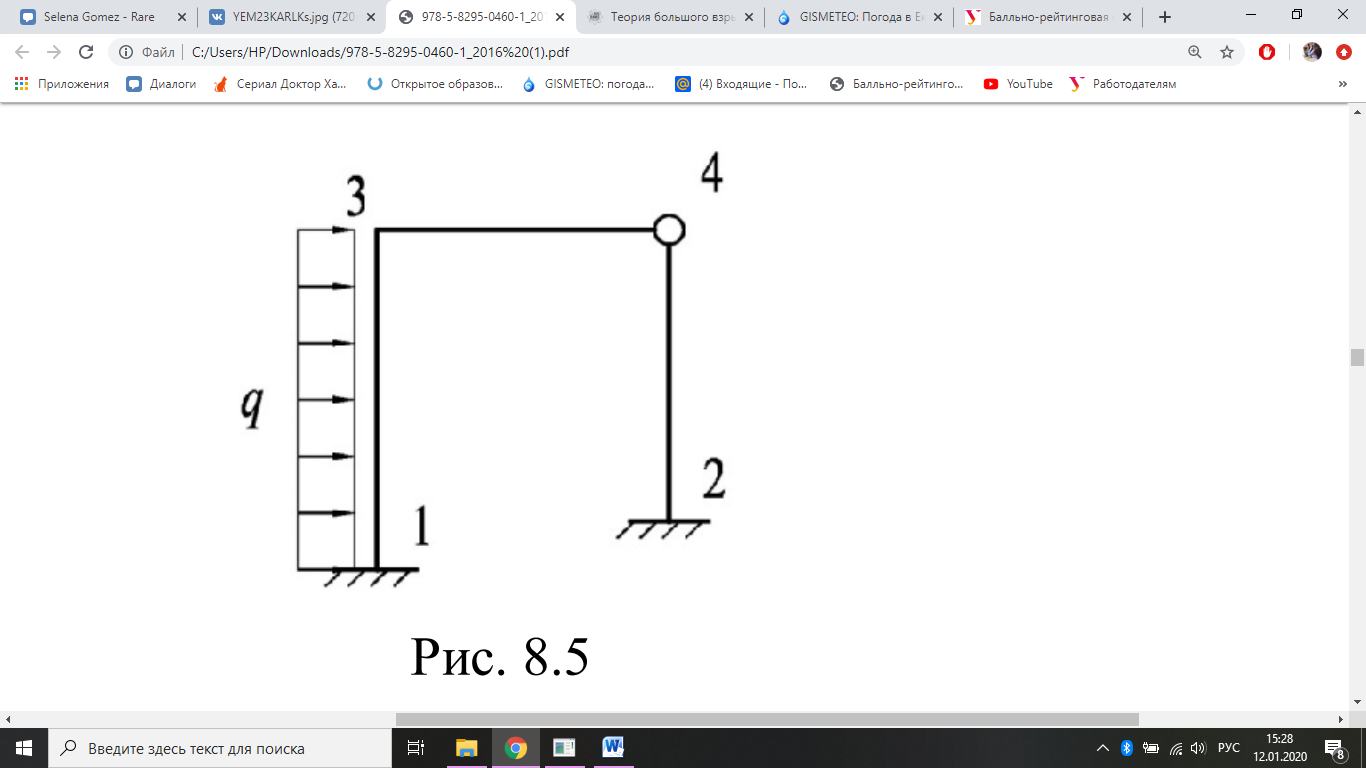
а рис. 2, нагруженной распределенной нагрузкой q.

Рис. 2

1. Заданная рама имеет один жесткий узел 3. При действии нагрузки этот

узел повернется на некоторый угол Z1. Одновременно узлы 3 и 4 переместятся линейно на величину Z2. Таким образом, рама имеет кинематическую неопределимость: K = K1 + K2 = 1 + 1 = 2.

2. Образуем основную систему. Для этого накладываем на жесткий узел 3

защемление I, препятствующее его повороту (рис. 3), а на уровне ригеля 3-4

в
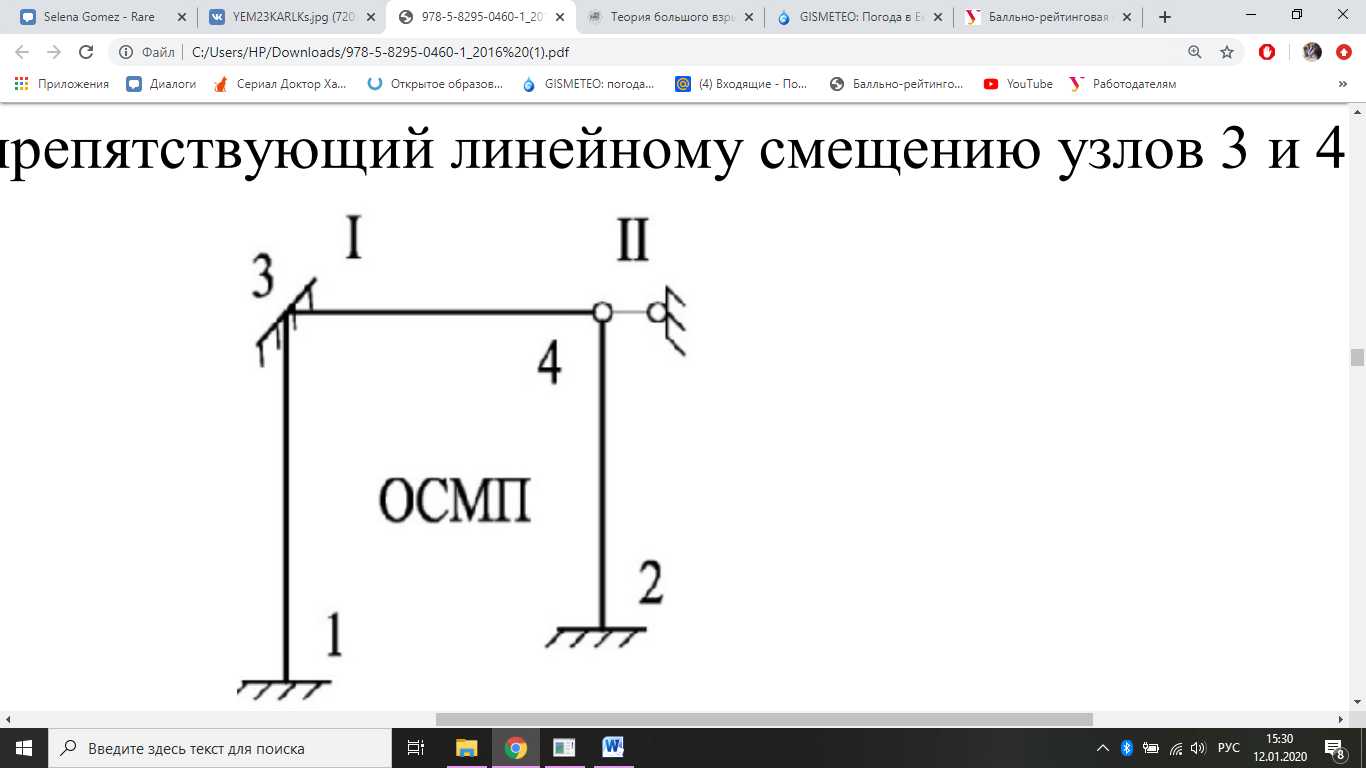
ведем стерженек II, препятствующий линейному смещению узлов 3 и 4.

Рис. 3

После введения связей рама распадается на совокупность статически

неопределимых балок двух типов: с двумя защемленными концами (рис. 4, а)

и
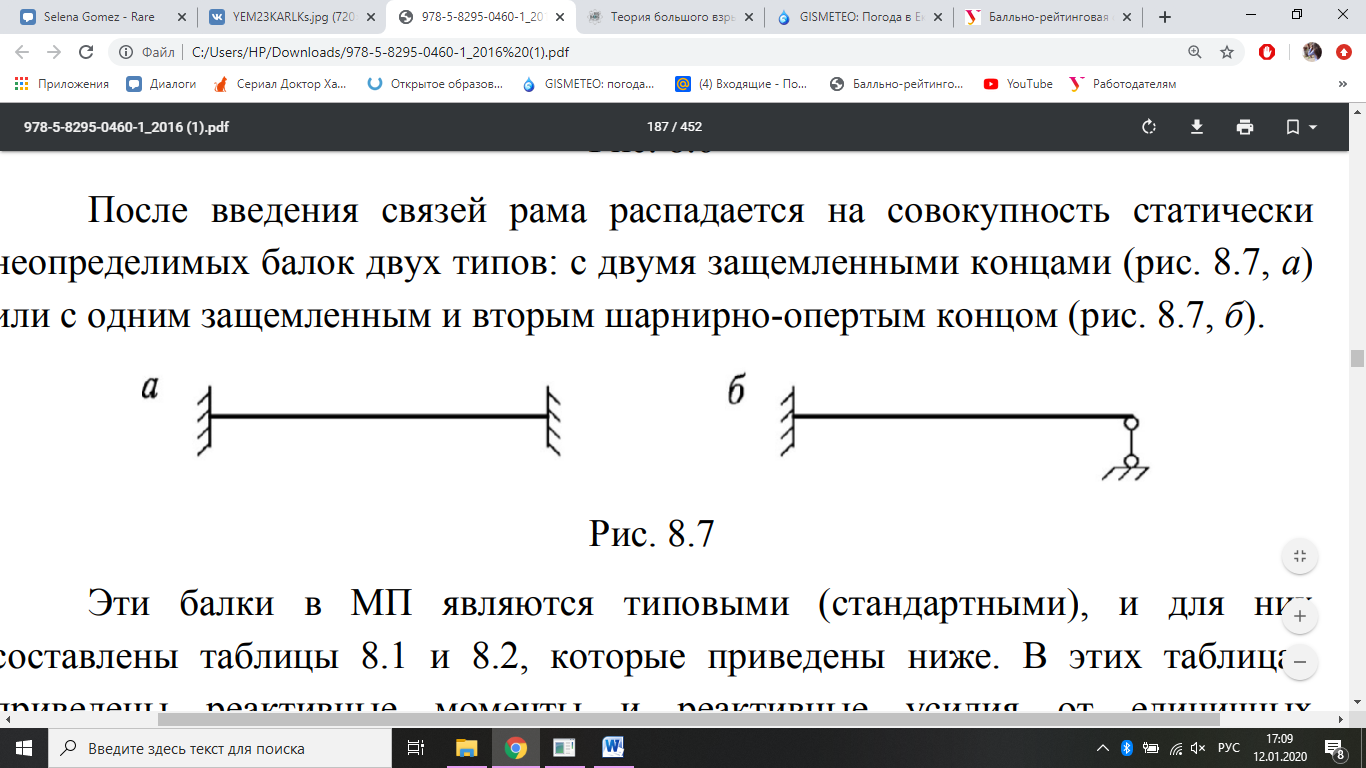
ли с одним защемленным и вторым шарнирно-опертым концом (рис. 4, б).

Рис. 4

Эти балки в МП являются типовыми (стандартными), и для них составлены таблицы. В этих таблицах приведены реактивные моменты и реактивные усилия от единичных перемещений связей и от внешней нагрузки.

Во введенных связях I и II возникают реактивные усилия RI и RII. Для обратного перехода от основной к заданной системе необходимо устранить

введенные связи. С этой целью повернем защемление I на действительный угол поворота Z1 (рис. 3), а связь II сместим на величину Z2. В результате от

д
ействительных смещений Z1 и Z2 в защемлении I и в стерженьке II возникнут реактивные усилия, равные по величине и противоположные по направлению усилиям R1p и R2p, полученным от внешней нагрузки. Так как в заданной системе защемления I нет и нет стерженька II, то реактивные усилия в них должны быть равны нулю. Это условие, отрицающее наличие реактивных усилий в наложенных связях I и II, в сжатой форме записи имеет вид:

Н
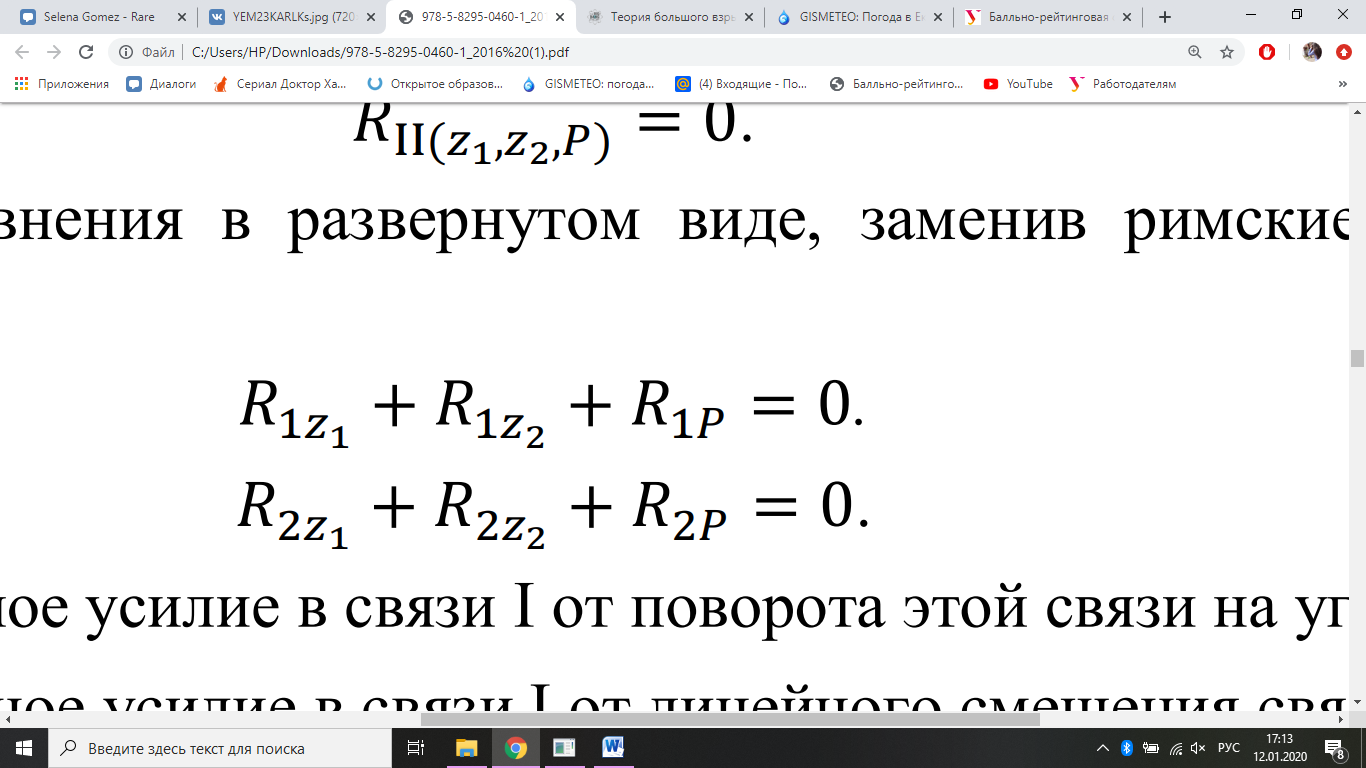
апишем уравнения в развернутом виде, заменив римские цифры на

арабские:

R_1z1 – реактивное усилие в связи I от поворота этой связи на угол z1;

R_1z2 – реактивное усилие в связи I от линейного смещения связи II;

R_1z1 – реактивное усилие в связи I от внешней нагрузки;

R_2z1, R_2z2, R_2P – соответственно в связи II.

В
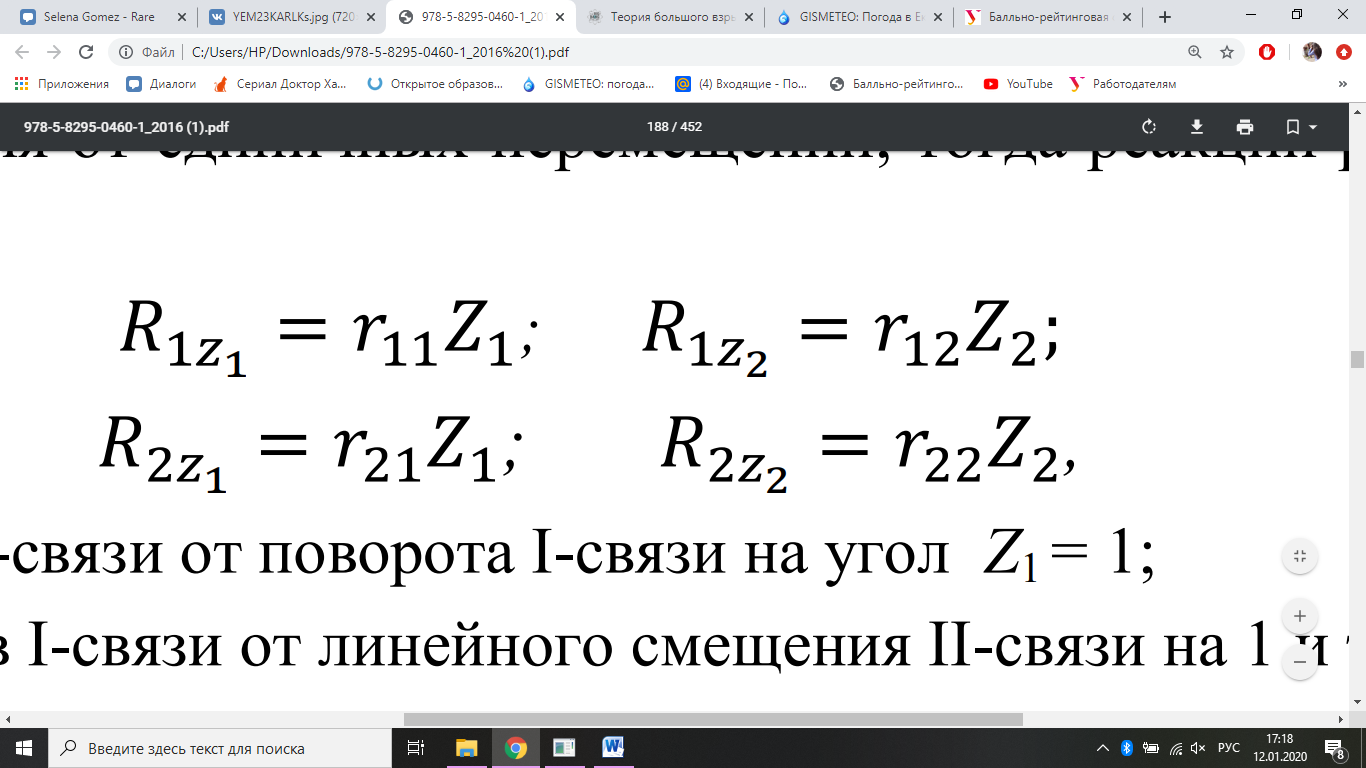
ведем усилия от единичных перемещений; тогда реакции распишутся в виде:

где r₁₁– усилие в I-связи от поворота I-связи на угол Z1 = 1;

r₁₂ – усилие в I-связи от линейного смещения II-связи на 1 и т. д.;

Z₁ – угол поворота жесткого узла 3;

Z₂ – линейное перемещение узлов 3 и 4 по горизонтали . При введении линейных связей следует иметь в виду, что они не всегда вводятся на уровне ригелей – «стерженек» может быть и вертикальным для препятствия вертикальному перемещению.

С
учетом изложенного уравнения приобретают вид:

В приведенном виде они представляют канонические уравнения при K = 2.

При K = 3 будет три уравнения. В коэффициентах уравнений первый индекс

показывает место, второй индекс – причину (перемещения), например, в коэффициенте r₂₁ это реактивное усилие в связи II, вызванное поворотом защемления I.

Если основная система содержит (n) дополнительных связей, то условие

э
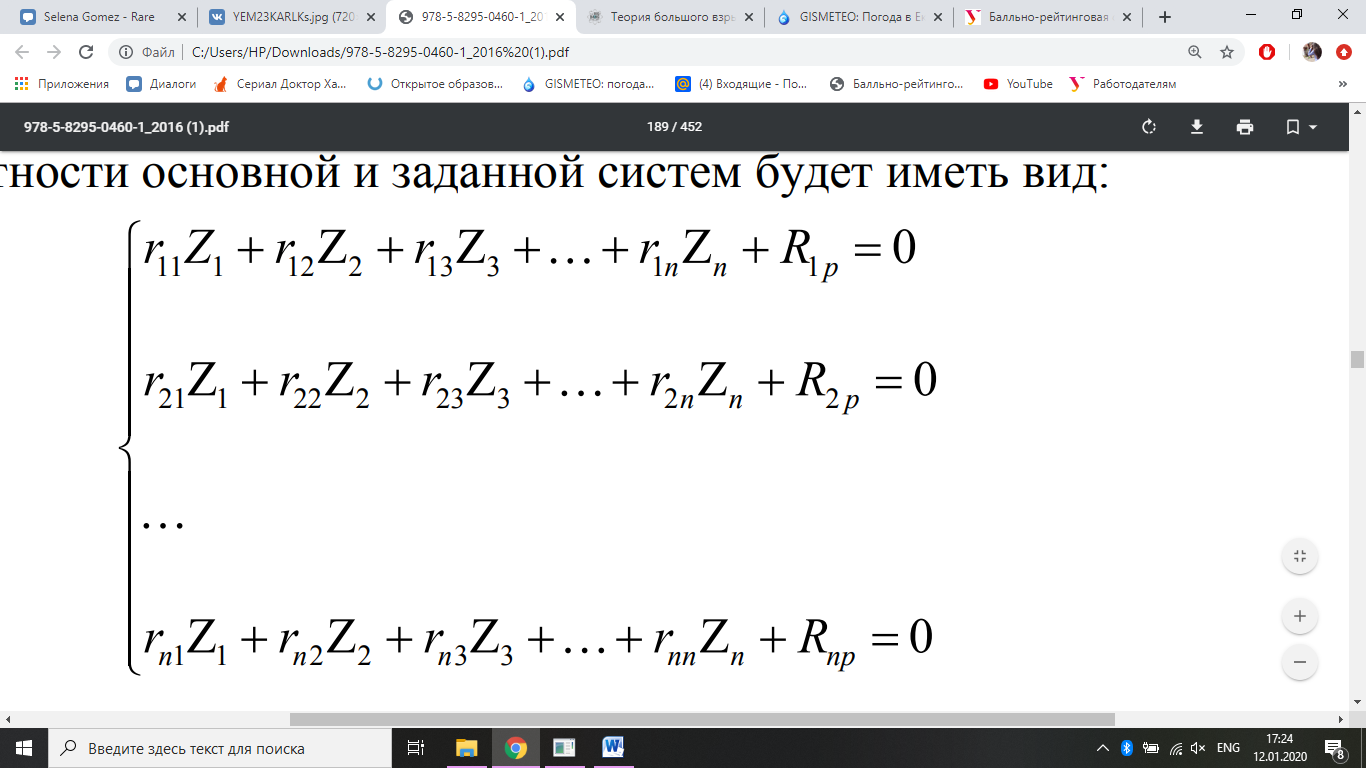
квивалентности основной и заданной систем будет иметь вид:

Полученные уравнения называются каноническими уравнениями метода

перемещений. Как было показано, в левой части любого i-го уравнения

записана суммарная реакция, возникающая в i-й связи. Коэффициенты r_ii,

стоящие на главной диагонали, а также определитель системы всегда положительны. Побочные коэффициенты указанной системы обладают

свойством взаимности: r_ik = r_ki.

Физический смысл канонических уравнений: каждое из уравнений

отрицает суммарную реакцию, возникающую в i-й связи от смещения

(линейного или углового) наложенных связей и от внешней нагрузки.

В канонические уравнения вошли коэффициенты rik и Rip, которые

зависят от реактивных усилий на концах различных статически неопределимых

балок, входящих в основную систему метода перемещений. Эти статически

неопределимые балки можно свести к трем типам:

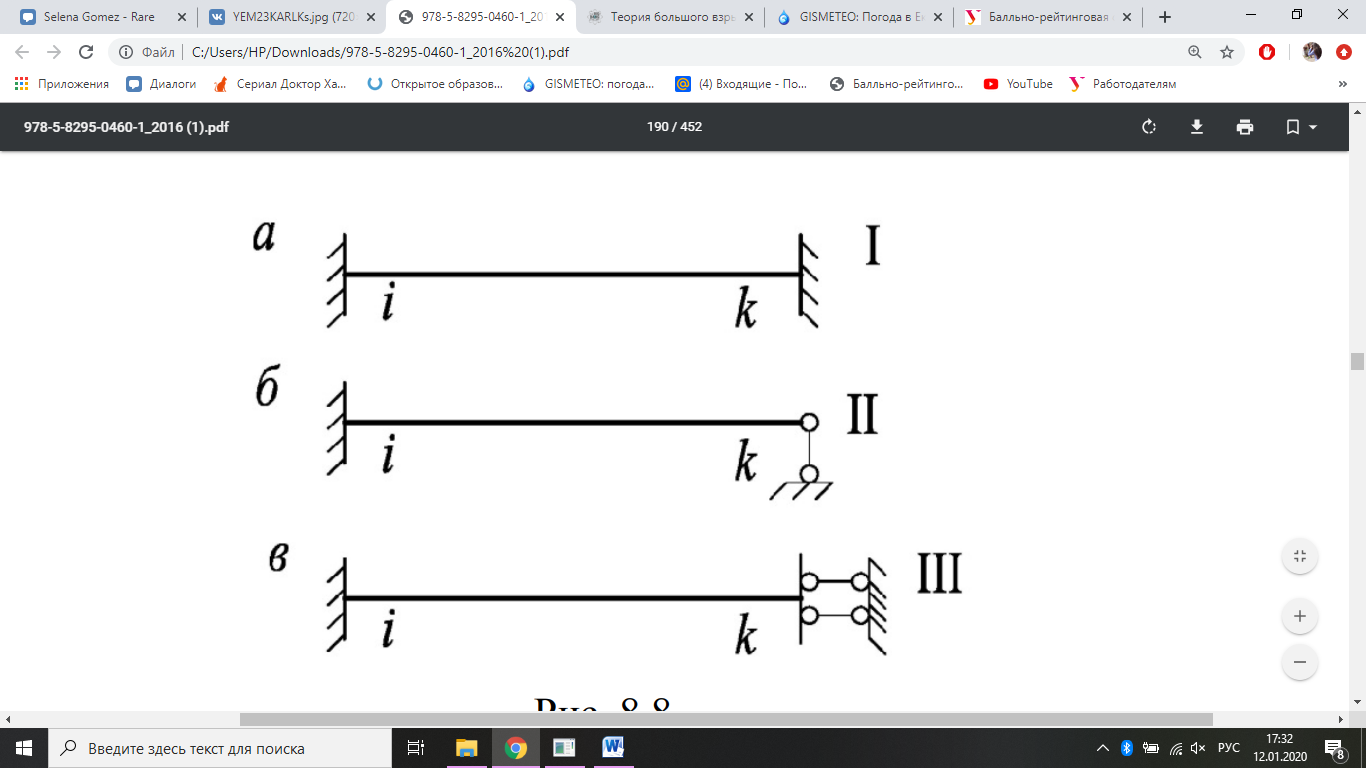
I – балка с двумя защемленными концами (рис. 5, а);

II – балка с одним защемленным концом и другим шарнирно опертым

(рис. 5, б);

III – балка с одним защемленным, другим концом в виде ползуна,

допускающего перемещение в направлении, перпендикулярном оси стержня (рис. 5, в).

Для этих типов балок определены реактивные усилия от единичных

с
мещений и внешней нагрузки, и результаты сведены в таблицы.
Рис. 5

2. Расчет рам на устойчивость

   1. 
      Общие положения
      

Наиболее эффективным методом расчета стержневых систем на устойчивость является метод перемещений. В отличие от метода сил, он требует меньшего числа неизвестных, обладает простотой определения коэффициентов канонических уравнений, однотипностью основной системы.

За неизвестные при потере устойчивости системы так же, как и при статическом расчете, принимаются углы поворота упругих узлов и их линейное

смещение. Для определения неизвестных, как и обычно, выбирается основная

система. Она получается в результате наложения на все внеопорные упругие

узлы защемлений, препятствующих их повороту, и закрепление узлов

стерженьками, устраняющими их линейное смещение.

В 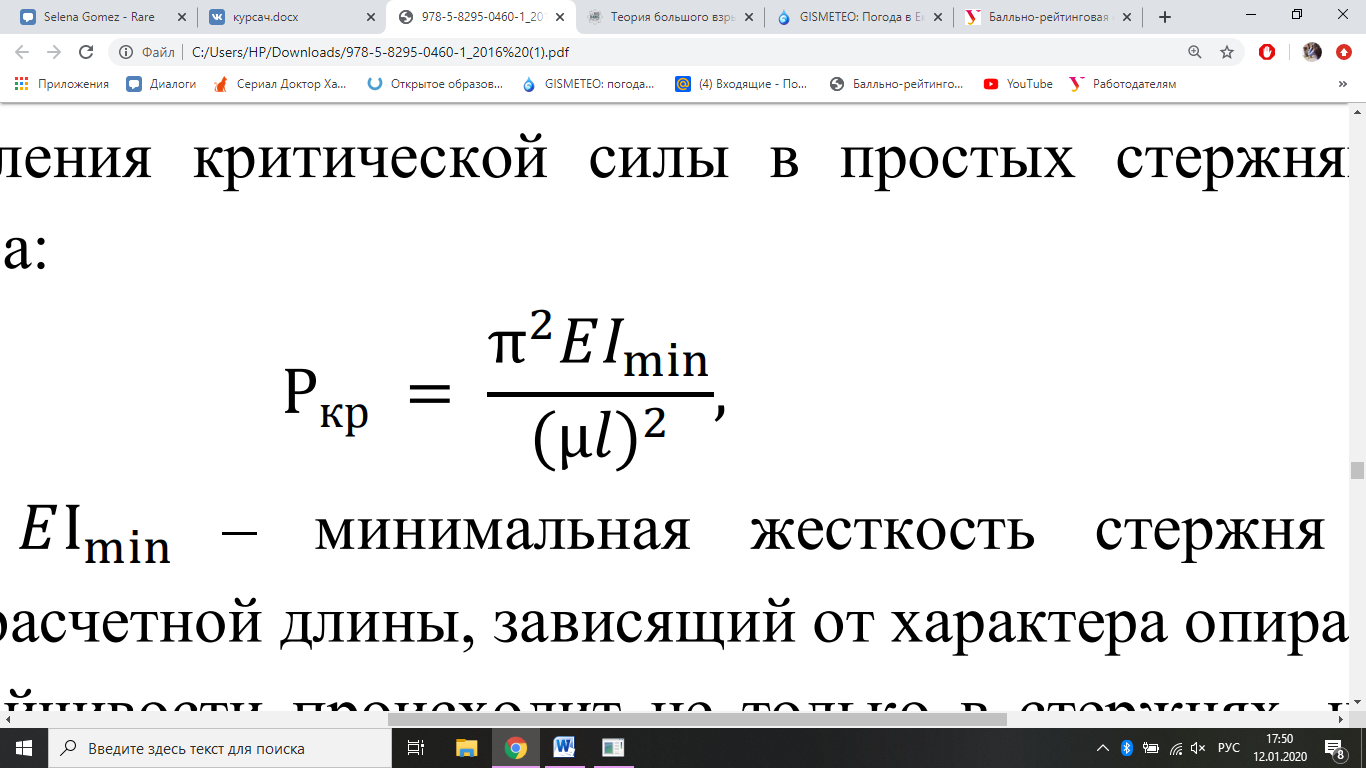рамах, кроме того, будем пренебрегать продольными и сдвигающими деформациями, обусловленными действием продольных и поперечных сил, а также сближением концов стержней. В момент потери устойчивости, в силу узловой передачи нагрузки, реактивные усилия от внешней нагрузки (свободные члены) в канонических уравнениях метода перемещений будут равны нулю. Для определения критической силы в простых стержнях используют формулу А. Эйлера:
где – длина; I – минимальная жесткость стержня при изгибе; μ – коэффициент расчетной длины, зависящий от характера опирания стержня.

Различают потерю устойчивости первого и второго рода. Потеря устойчивости первого рода при постепенном статическом возрастании нагрузки происходит внезапно и сопровождается появлением и развитием совершенно новых форм деформации. Потеря устойчивости второго рода происходит в результате развития предшествующих деформаций, без появления новых форм деформации, вследствие невозможности поддержания статического равновесия между внешними нагрузками и внутренними силами системы.
П ри расчете рам (рис. 6) действующие внешние усилия пропорциональны одному параметру Р (k1 и k2 – коэффициенты пропорциональности). На рис. 6, а представлена местная форма потери устойчивости, а на рис. 6, б – общая. В этом случае под критическим Р = Ркр следует понимать тот наименьший параметр критической системы сил, при котором наблюдается переход исходной системы из прямолинейной в смежную искривленную форму равновесия (статический критерий).

Рис. 6

М естная форма выпучивания, как правило, наблюдается в рамах с линейно-неподвижными узлами, а общая – в рамах с линейно-подвижными узлами. В реальных конструкциях любое сжимающее усилие N в стойках должно быть меньше критического параметра для рамной системы
т. е. должен быть обеспечен запас устойчивости сооружения:







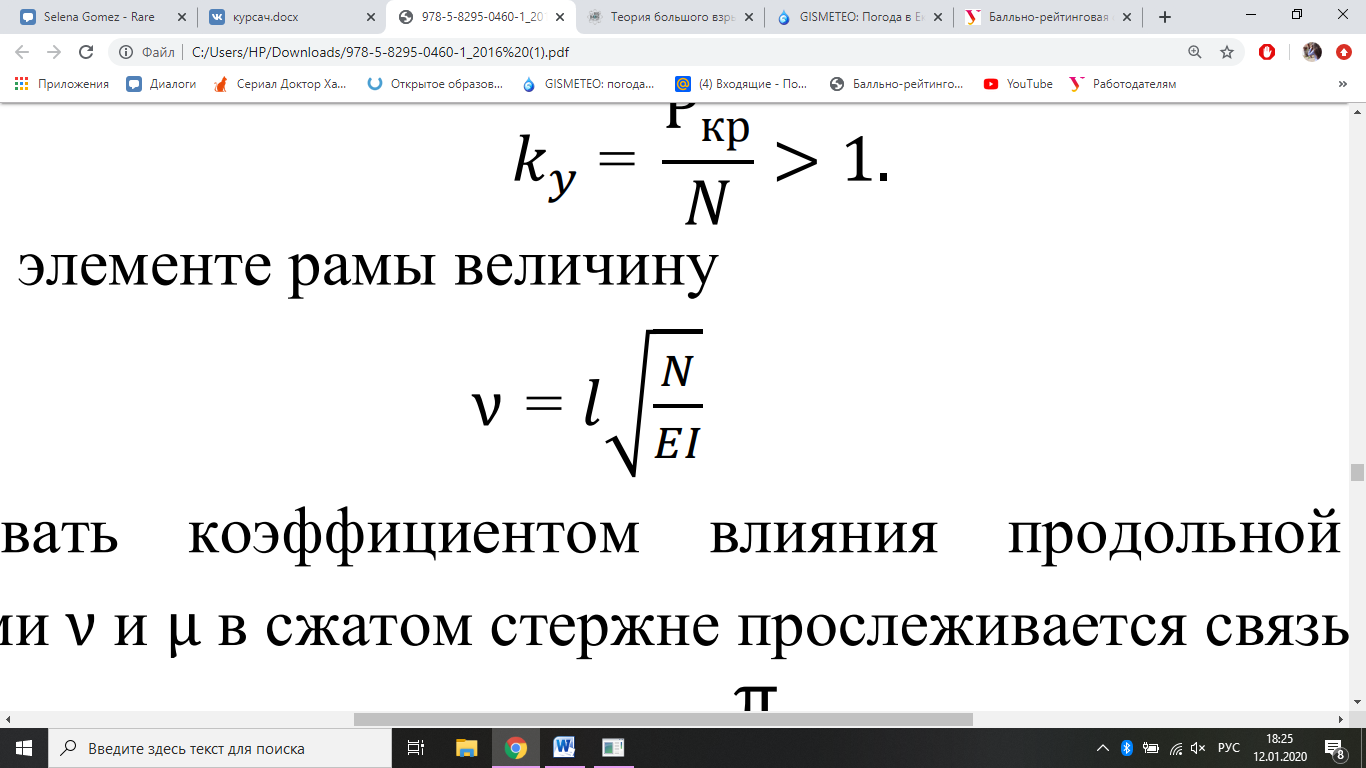
В сжатом элементе рамы величину

п ринято называть коэффициентом влияния продольной силы. Между коэффициентами ν и μ в сжатом стержне прослеживается связь ν = π/ μ . Коэффициент μ необходим для определения гибкости сжатого стержня




где – минимальный радиус инерции поперечного сечения;

i 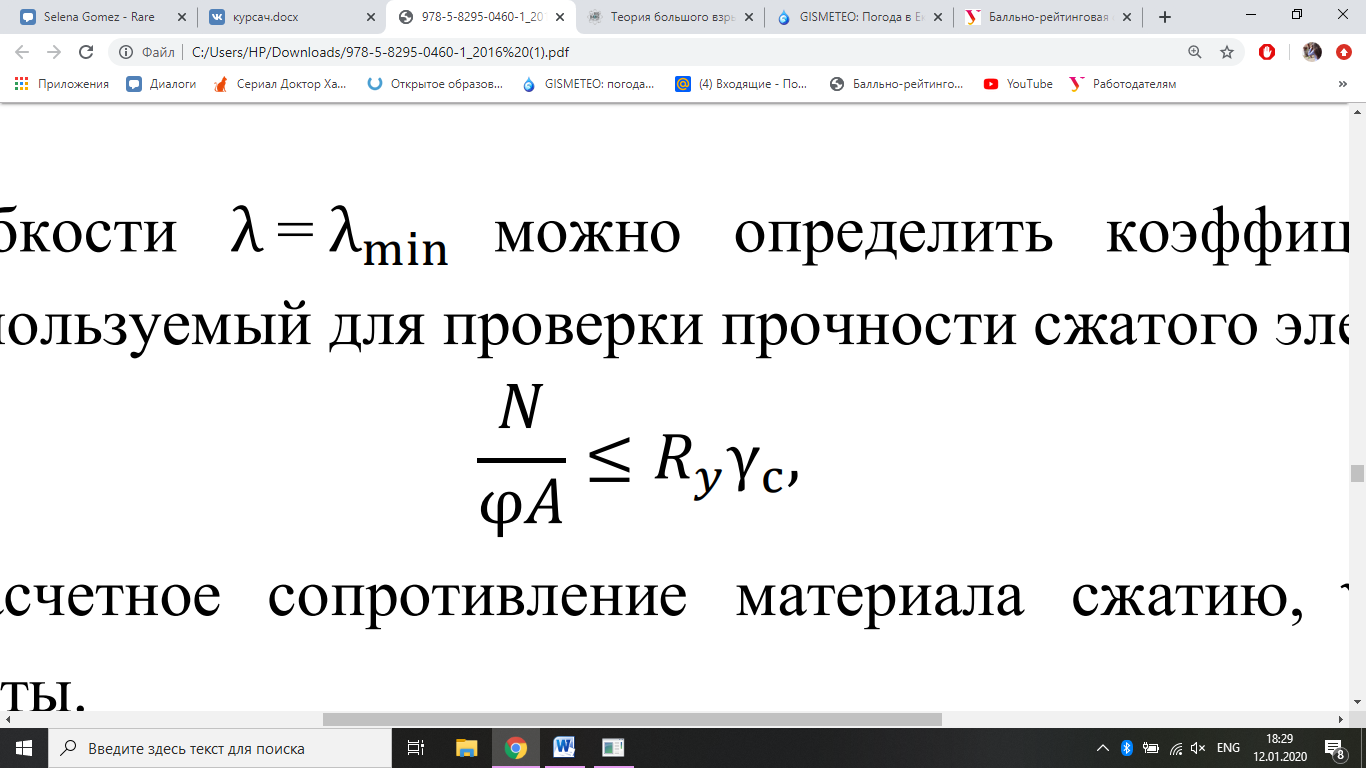_min– минимальный центральный момент инерции; А – площадь поперечного сечения. По гибкости λ = λ_min можно определить коэффициент продольного изгиба φ, используемый для проверки прочности сжатого элемента рамы:
г 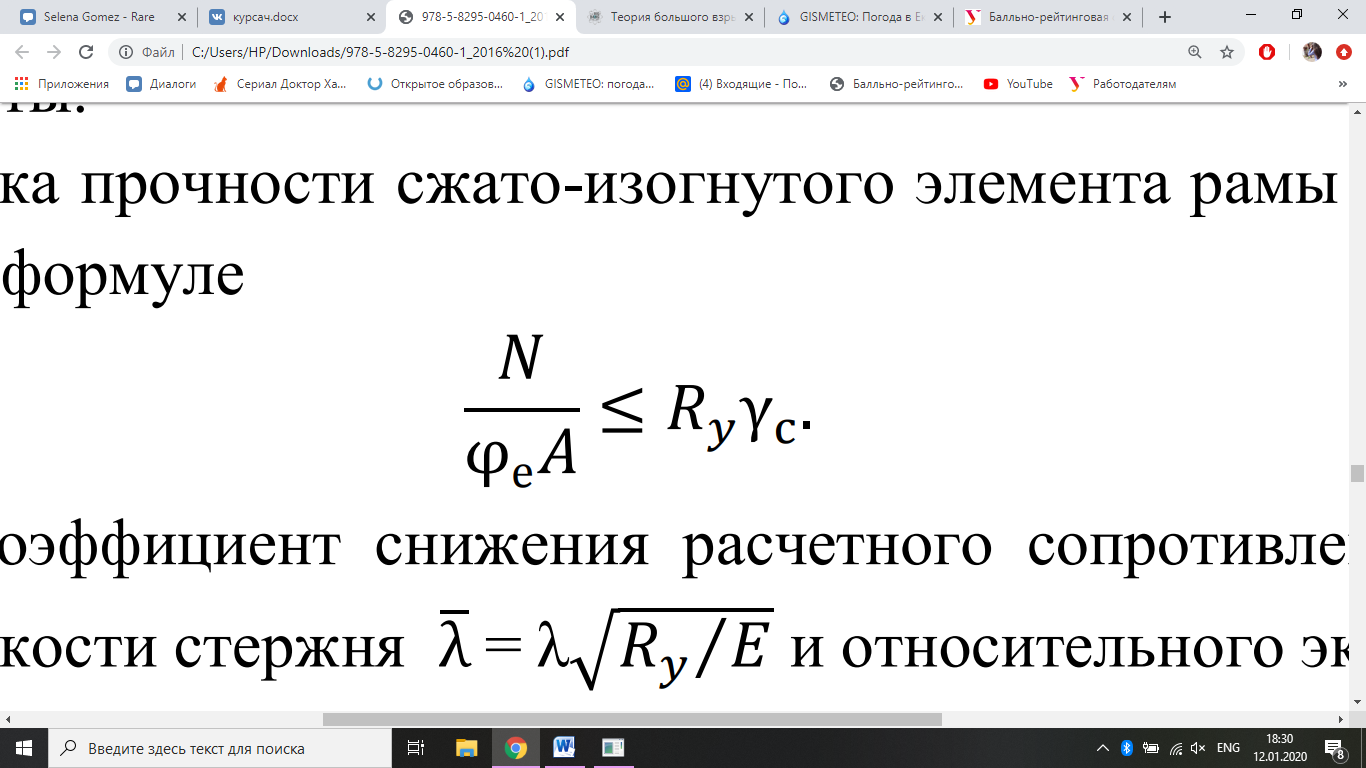де – расчетное сопротивление материала сжатию, γ – коэффициент условий работы. Проверка прочности сжато-изогнутого элемента рамы осуществляется по аналогичной формуле
З десь φе – коэффициент снижения расчетного сопротивления, зависящий от условной гибкости стержня и относительного эксцентриситета



где η – коэффициент влияния формы сечения (см. таблицу Д.2 СП16.13330.2011). Если действующие на сооружение нагрузки различны по своему характеру (собственный вес, снеговая нагрузка и др.), т. е. нагружение является многопараметрическим, то приходится выявлять серию критических значений Ркр, соответствующих различным сочетаниям нагрузок.

2. 
   Основные понятия
   

В предыдущей главе было рассмотрено применение метода перемещений (МП) для расчета рам на прочность. Этот метод оказался эффективным и для расчета рам на устойчивость. Для использования МП в расчетах на устойчивость были выведены формулы реакций от единичных воздействий для типовых стержней, работающих на сжатие. Формулы реакций сжатых стержней аналогичны формулам табл. 8.1, но от выражений этой таблицы указанные реакции в типовых стержнях отличаются наличием специальных функций ( 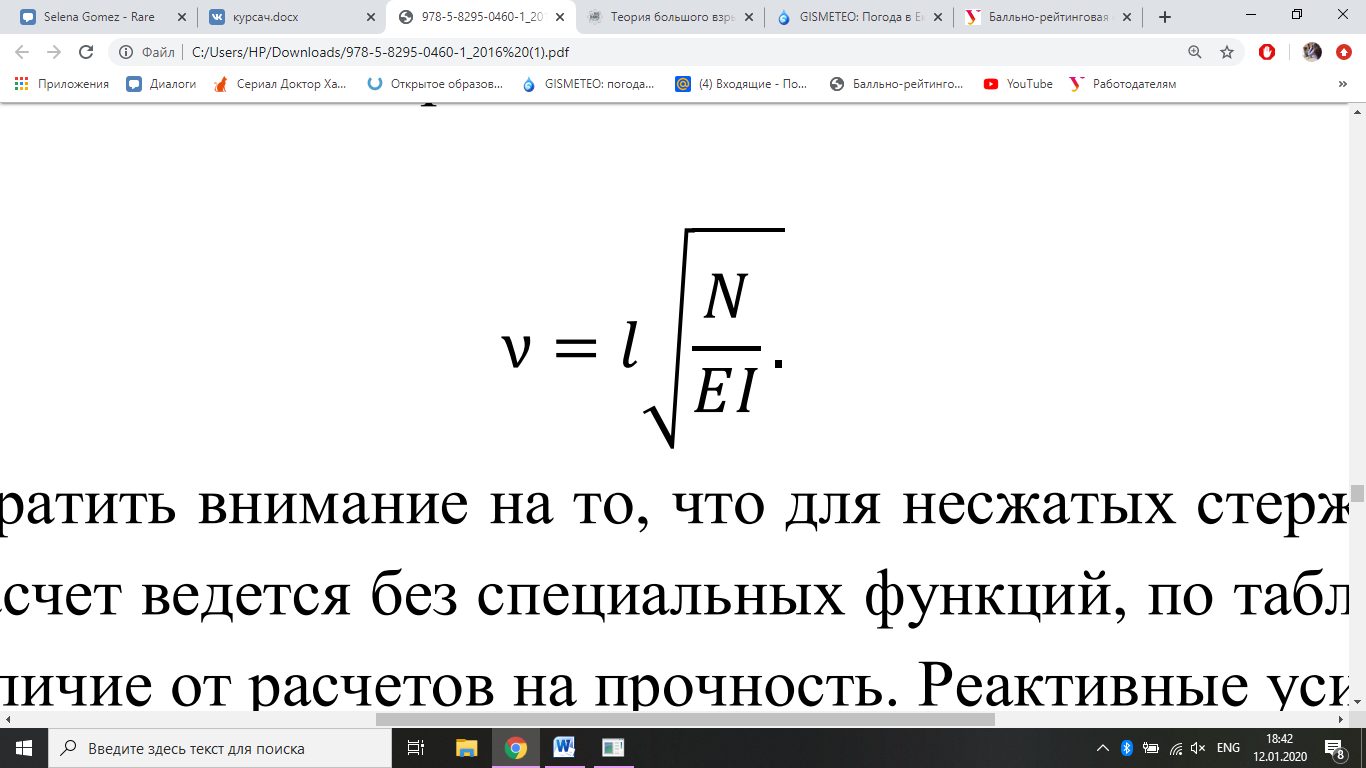функции Н. В. Корноухова). Эти функции зависят от параметра ν, который называется коэффициентом влияния продольных с ил и определяется для каждого сжатого элемента по формуле:

Следует обратить внимание на то, что для несжатых стержней, входящих в состав рамы, расчет ведется без специальных функций, по табл. 8.1. Еще одна особенность – отличие от расчетов на прочность. Реактивные усилия возникают и в статически определимых сжатых элементах (табл. 9.1, строки 7, 8.). Специальные функции вычислены для конкретных значений ν от 0 до 2π приведены в табл. 9.2. При расчете на устойчивость на раму действуют только внешние сжимающие силы, направленные вдоль сжатых элементов, и система канонических уравнений МП не имеет свободных членов. В результате получаем уравнение устойчивости в виде определителя D(ν) = 0:




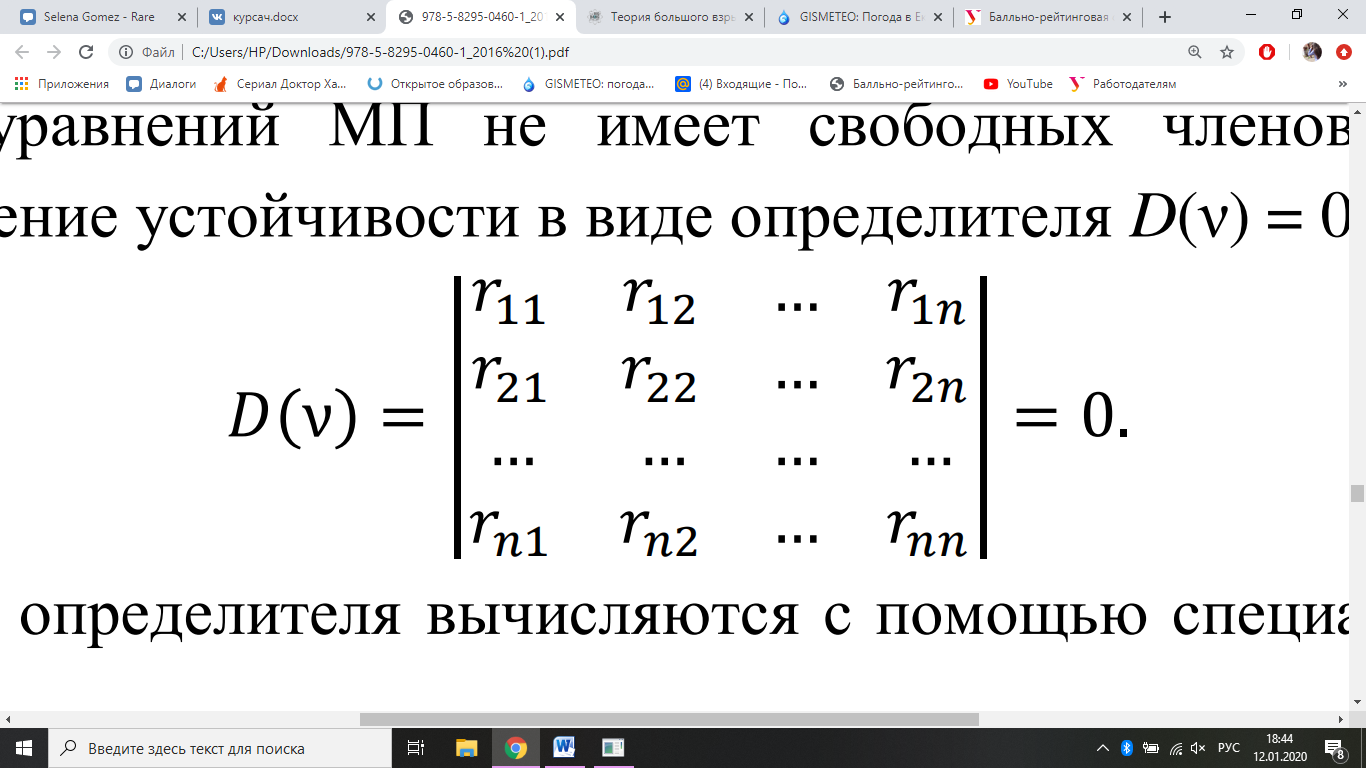
Элементы определителя вычисляются с помощью специальных функций (табл.9.1).

При расчете рам их подразделяют на рамы с неподвижными и линейноподвижными узлами, а также рамы с бесконечно жесткими ригелями.

3. Свободные колебания системы с двумя и несколькими степенями свободы

Д ля системы с n степенями свободы уравнения описываемых колебаний имеют вид:

В матричном виде эти уравнения записываются:




- собственное число матрицы А*



- собственный вектор матрицы А*. Количество таких векторов равно порядку матрицы A*
С истема представляет собой систему однородных алгебраических уравнений относительно координат векторов. Она может иметь не нулевое решение, если определитель этой системы равен нулю, то есть:

Уравнение называется характеристическим уравнением матрицы А*. Собственные числа λ называются характеристическими. В развернутом виде уравнение имеет вид:




Е сли определитель раскрыть, то получим уравнение n-ой степени относительно λ:

Решая это уравнение, получим спектр собственных λ1 > λ2 > λ3 … > λn и соответствующие частоты ω1 < ω2 < ω3 …< ωn.

П ри решении этого уравнения используется численная процедура отыскания λi, основу которой составляет построение зависимости det()от λ посредством ЭВМ (рис. 7)

Рис. 7

К аждому характеристическому числу λi соответствует свой собственный вектор V(i =1,2,3,... n ) и уравнению будет соответствовать n равенств Таким образом, решение задачи о свободных колебаниях системы с n степенями свободы сводится к определению всех характеристических чисел λi и всех собственных векторов Vi, по характеристическим числам λi определяются частоты системы

Примечания: 1. Характеристические числа всегда вещественны и положительны (λi > 0).

2 . Сумма λi равна следу матрицы А*, то есть сумме ее членов по главной диагонали:

3 . Произведение λi равно определителю матрицы А*:
По найденным λi определим частоты ωi . При любой частоте вековое уравнение должно быть удовлетворено, и определитель D обращается в ноль. Каждой частоте соответствует своя совокупность D значений амплитуд Ai (координат собственных векторов V  ). Амплитуды (амплитудные коэффициенты) обозначаются с двумя индексами – Аki. Первый индекс указывает номер координаты перемещения массы yi , а второй – номер частоты.

П одставив λi в уравнение вместо λ, получим следующую систему однородных уравнений для определения амплитудных коэффициентов. Если в этой системе все члены разделить, например, на и обозначить отношение

то получим новую систему уравнений.




Отсюда определяются отношения , которых будет на единицу меньше числа уравнений. Одно из уравнений будет линейной комбинацией остальных и может быть отброшено.

О пределив частоты собственных колебаний и амплитудные коэффициенты (координаты собственных векторов), можно построить общее решение дифференциальных уравнений свободных колебаний. Для системы с n степенями свободы общее решение можно записать в виде:
где = 1, 2, 3, …, n. Отсюда следует, что колебания с n степенями свободы носят сложный многочастотный характер. Каждой собственной частоте соответствует своя особая форма колебаний. Под формой колебаний понимают характер изогнутой оси стержня (стержневой системы). Колебания, соответствующие наименьшей частоте ω , называются колебаниями основного тона, а остальные (в порядке возрастания частот) – колебаниями второго, третьего и т. д. тонов или обертонов.

При колебаниях системы с n степенями свободы отношения перемещений отдельных масс меняются с течением времени. Однако можно так подобрать начальные условия движения системы, при которых все массы системы будут колебаться с одинаковой частотой. Колебания и соответствующие им формы, при которых все массы колеблются с одинаковой частотой, называются главными или нормальными.

---

Смотрите также файлы

• Правила для велосипедистов проверка домашнего задания.ppt

• Практическая работа по дисциплине Операционные системы студент 3 курса факультета программная инженерия.docx

• Неклассические коллектора виды, процессы образования, распространения.doc

• Методы исследования структуры кристаллов.ppt

• Электронные ресурсы.docx