Министерство цифрового развития, связи и
массовых коммуникаций Российской Федерации

Сибирский государственный университет телекоммуникаций и информатики
Межрегиональный учебный центр переподготовки специалистов
Лабораторная работа №1

по дисциплине:

«Теория электрических цепей»

Выполнил: Перфильев С.Е. Группа: МБТ-22

Вариант: 6

Проверила: Дежина Е.В.

Новосибирск, 2023 г.

Лабораторная работа № 1

Исследование реактивных двухполюсников
1.  Цель работы

Исследование зависимости входного сопротивления реактивного двухполюсника от частоты.
2.  Подготовка к выполнению работы

При подготовке к работе необходимо изучить теорию реактивных двухполюсников, методы их анализа и синтеза (параграфы 4.5 и 16.6 электронного учебника).
3.  Экспериментальная часть

3.1. Собрать схему реактивного двухполюсника (рисунок 3.1, а), изображенного по 1-й форме Фостера. В программе Electronics Workbench 5.12 схема имеет вид, приведенный на рисунке 3.2, б. Установить E= 1 В, f= 1кГц, R₀ = 10 кОм, L₁ = L₂ = 1 мГн, C₁ = 63,536 нФ, С₂ = 15,831 нФ, С = (100+N×5) нФ, где N — номер варианта (последняя цифра пароля).

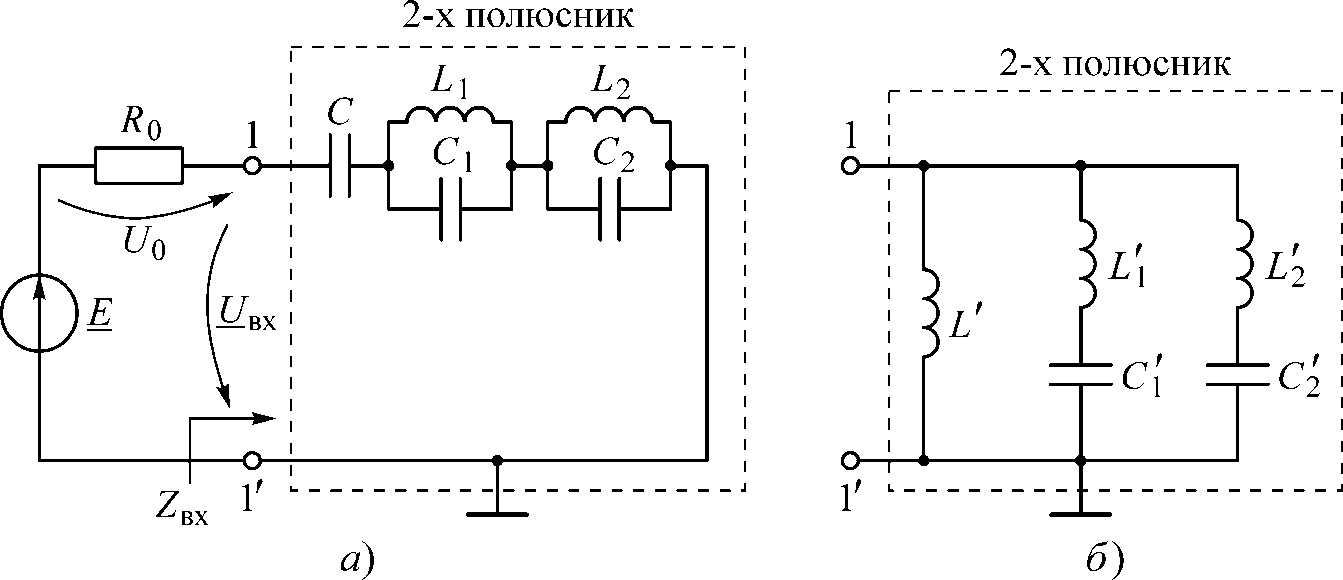
Рисунок 3.1
а)
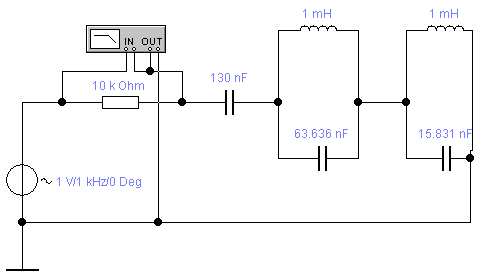
б)
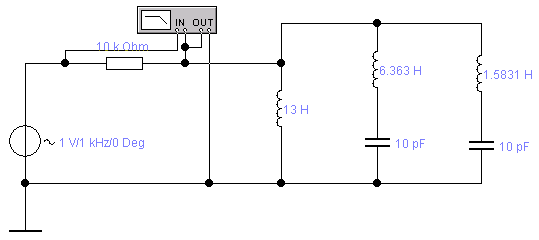
Рисунок 3.2

3.2.  Подключить прибор BodePlotter (измеритель коэффициента передачи Н по напряжению от частоты) следующим образом:

• 
  Гнезда IN — к резистору R₀ (для измерения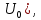 гнезда OUT — к входу реактивного двухполюсника — точки 1–1’ (для измерения U_вх). Установить следующие настройки прибора:
  
• 
  Линейный масштаб LINпо вертикали и горизонтали;
  
• 
  По вертикали масштаб шкалы 0 –1;
  
• 
  По горизонтали масштаб шкалы 0,1 мГц – 80 кГц.
  

---

В этом случае на экране прибора будет отображаться частотная характеристика H(f)=U_вх(f)/U₀(f), которая пропорциональна входному сопротивлению двухполюсника.

Входное сопротивление при этом определяется косвенным методом по формуле:



3.3.  В диапазоне частот 0,1 мГц – 80 кГц на частотах резонансов и по одной частоте между резонансами измерить и записать в таблицу 3.1 значения Н. Рассчитать по формуле 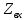(Ом) входное сопротивление реактивного двухполюсника и также записать в таблицу 3.1.
Таблица 3.1

f, кГц	f1	f2	fрез1	f4	fрез2	f6	fрез3	f8	fрез4	f10	f11
	0	4	9,16	15	19,97	23	25,99	33	40	60	80
Н	∞	0,025	0	0,024	3,77	0,028	0	0,049	915	0,037	0,022
Zвх	∞	254	0.019	244	37740	279	0,302	492	9·106	369	216

3.4.  Определить параметры элементов обратного двухполюсника (рисунки 3.1, б и 3.2, б) по формулам:

---

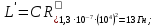
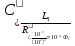
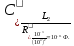
Собрать схему обратного двухполюсника (рисунки 3.1, б и 3.2, б), подключить прибор Bode plotter и произвести измерения согласно п.п. 3.2, 3.3. Данные измерений и расчетов записать в таблицу аналогичную таблице 3.1.

Таблица 3.2

f, кГц	f1	f2	fрез1	f4	fрез2	f6	fрез3	f8	fрез4	f10	f11
	0	4	9,16	15	19,97	23	25.99	33	40	60	80
Н	0	39,3	5,24 ×105	40,9	9,62 ×10–4	35,8	6,05 ×105	20,3	1,09 ×10–3	27,1	46,2
Zвх	0	3,93 ×105	5,24 ×109	4,09 ×105	9,62	3,58 ×105	6,05 ×109	2,03 ×105	10,9	2,71 ×105	4,62 ×105

3.5.  По результатам расчета Z_вх(f) построить в масштабе графики зависимости модуля входного сопротивления исходного и обратного реактивных двухполюсников от частоты и указать на них частоты резонансов напряжений и токов.




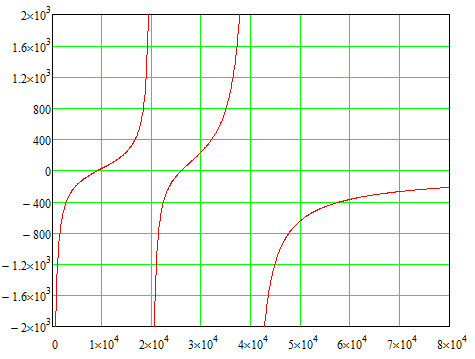
Рисунок 3.3 — График зависимости реактивного входного сопротивления исходного двухполюсника



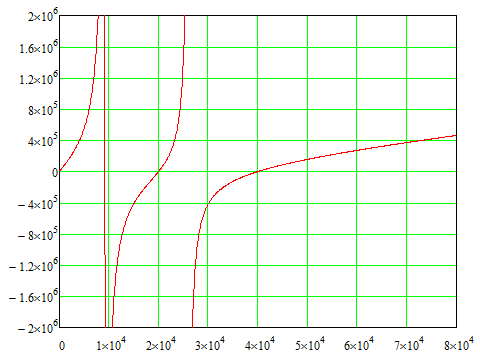
Рисунок 3.4 — График зависимости реактивного входного сопротивления обратного двухполюсника

---

Выражения , записанные через резонансные частоты.
Входное сопротивление исходного реактивного двухполюсника:



где


Входная проводимость обратного реактивного двухполюсника:

где,


4.  Выводы

В работе исследовались зависимости модуля входного сопротивления реактивных двухполюсников от частоты.

Исходный двухполюсник представляет собой последовательное соединение емкости и двух параллельных контуров без потерь. Такой двухполюсник имеет четыре резонансных частоты.

Обратный двухполюсник представляет собой параллельное соединение индуктивности и двух последовательных контуров. У него также имеется четыре резонансных частоты.

Резонансные частоты исходного и обратного двухполюсников совпадают, но имеют разный характер (частота резонанса напряжений исходного двухполюсника является частотой резонанса токов двухполюсника обратного, и частота резонанса напряжений исходного двухполюсника является частотой резонанса токов обратного).

---

Смотрите также файлы

• Лабораторная работа 4.docx

• 2 Выберите один, наиболее правильный вариант. В селекции животных практически не используют.docx

• .docx

• Потребительские сегменты.docx

• Разработка эксплуатационной документации на программное средство.doc