ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Индивидуальные задания
Задание 1. Представить число -69,223 в машинном виде с использованием
4 байтового представления (где 1 бит отводится под знак числа,
8 бит – под смещенный порядок, остальные биты – под мантиссу)
и их 16-ричную форму.
Решение:
| | Остаток |
| 69:2=34 | (1) |
| 34:2=17 | (0) |
| 17:2=8 | (1) |
| 8:2=4 | (0) |
| 4:2=2 | (0) |
| 2:2=1 | (0) |
6910 = 10001012
0,223*2=0,446
0,446*2=0,892
0,892*2=1,784
0,784*2=1,568
0,568*2=1,136
0,136*2=0,272
0,272*2=0,544
0,544*2=1,088
0,088*2=0,176
0,176*2=0,352
0,352*2=0,704
0,704*2=1,408
0,408*2=0,816
0,816*2=1,632
0,632*2=1,264
0,264*2=0,528
0,528*2=1,056
0,056*2=0,112
0,112*2=0,224
0,224*2=0,448
0,448*2=0,896
0,896*2=1,792
0,792*2=1,584
0,584*2=1,168
0,22310=0011100100010110100001112
101000101, 001110010001011010000112 = 1,010001010011100100010110100001112 *26
СП = 127+6=133
| - | 4 | 5 | 3 | 9 | 1 | 6 | 8 | 7 | ||||||||||||||||||||||||||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||||||
Ответ: -45,39168716.
Задание 2. Составьте программу на языке Pascal для представления введенного отличного от нуля действительного числа в нормализованной форме.
Решение в файле задание 2.pas.
Задание 3. Составьте программу на языке Pascal для представления введенного числа в машинном виде с использованием 4 байтового представления.
Решение в файле задание 3.pas.
Контрольные вопросы
1. Каким образом вещественные числа представляются в современных компьютерах.
Для представления вещественных чисел в современных компьютерах принят способ представления с плавающей запятой. Этот способ представления опирается на нормализованную (экспоненциальную) запись действительных чисел.
Как и для целых чисел, при представлении действительных чисел
в компьютере чаще всего используется двоичная система, следовательно, предварительно десятичное число должно быть переведено двоичную систему.
2. Что понимают под нормализованной записью числа.
Нормализованная запись отличного от нуля действительного числа - это запись вида a= m*Pq , где q - целое число (положительное, отрицательное или ноль), а m - правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть
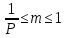. При этом m называется мантиссой числа,P – основание системы счисления, q - порядком числа.
3. Какой вид имеет нормализованная экспоненциальная запись числа.
Нормализованная экспоненциальная запись числа - это запись вида a= m*Pq, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом (m-целая часть) называется мантиссой числа, q - порядком числа.
4. Опишите способ представлении чисел с плавающей запятой в ЭВМ.
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, был придуман так называемый смещённый порядок. Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.
5. Каким образом рассчитывается смещенный порядок.
Если для задания порядка выделено к разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2 к-1 - 1).
Например, порядок, принимающий значения в диапазоне от —128 до +127, представляется смещенным порядком, значения которого меняются
от 0 до 255. Использование смещенной формы позволяет производить операции над порядками как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также операцию сравнения самих нормализованных чисел.
6. Опишите алгоритм представления числа с плавающей запятой.
1) перевести число из p-ичной системы счисления в двоичную;
2) представить двоичное число в нормализованной экспоненциальной форме;
3) рассчитать смещѐнный порядок числа;
4) разместить знак, порядок и мантиссу в соответствующие разряды
сетки.