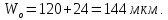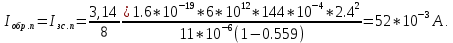Выбираем 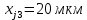, а из этого следует, что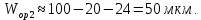

Далее рассчитываем постоянную времени нарастания прямого тока 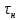, как положительный корень уравнения ниже:
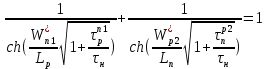(18)
Время жизни дырок в n₁ – базе рассчитано по формуле (9), а время жизни электронов в p₂ – базе обычно принимается равным (0.1 – 0.4)* 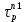. Диффузионные длины дырок в n₁ – базе и электронов в p₂ – базе рассчитываются по следующим формлуам:
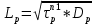(19)

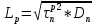(20)
где Dn и Dp – коэффициенты диффузии электронов и дырок. При температуре 20 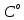D_n = 33 см²/с и D_p = 12 см²/с, при температуре 125 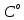D_n = 22 см²/с и D_p = 8 см²/с.

Примем



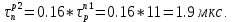
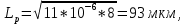
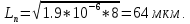
Постоянную времени нарастания прямого тока определяют графически. Построение графика идёт по следующей функции:
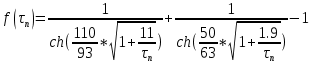(21)
График построенный по этой функции в MathCad показан ниже:

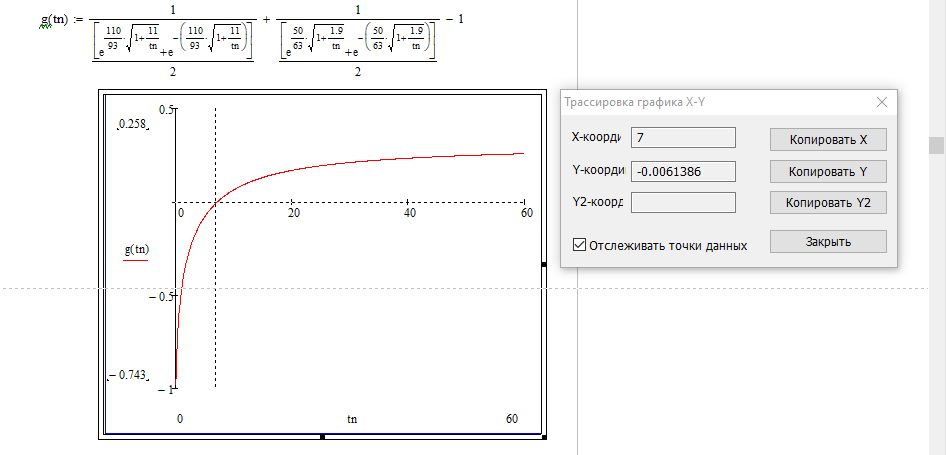
Рисунок 2 – Определение
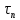
Исходя из данного графика постоянная времени нарастания тока

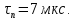
Рассчитав постоянную времени нарастания прямого ток, вычислим плотность критического заряда включения тиристора, обеспечивающую заданное значение:
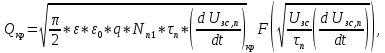(22)
Интеграл вероятности функции ошибок, определяется по графику ниже:

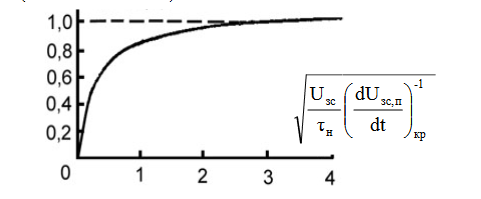
Рисунок 3 –

---

Интеграл вероятности ошибок



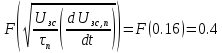
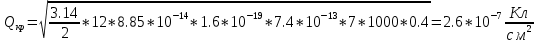
Теперь рассчитаем плотность тока утечек через переход :
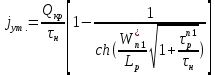(23)
.
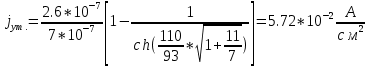Рассчитаем удельное сопротивление и концентрацию акцепторов в p₂ – базе:
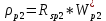(24)
Обычное значение 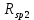для тиристоров от 200 до 400 Ом. Выбираем 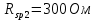, тогда удельное сопротивление равно: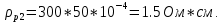

Зная удельное сопротивление 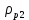мы можем определить концентрацию акцепторов в p₂ – базе по графику зависимости .

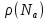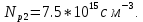
Посчитаем равновесную концентрацию электронов – базе при пределельной температуре 125 ^оС. Учтём что при 20 ^оС собственная концетрация носителей в кремнии 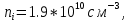а при предельной температуре :
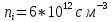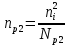(25)
.
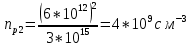Рассчитаем коэффициент переноса дырок через – базу:
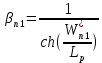(26)



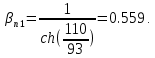
Рассчитаем коэффициент переноса электронов через p₂ – базу:
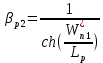(27)


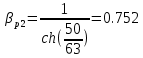
Рассчитаем плотность тока насыщения через переход

---

при предельной температуре:
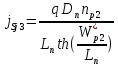(28)


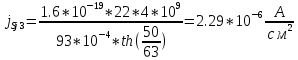
Теперь рассчитаем сопротивление технологической шунтировки единицы площади третьего перехода j₃. Шунты нужны для замыкания эммитерного перехода тиристора и улучшения прямого напряжения пробоя и стойкости.
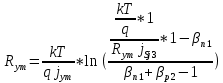(29)
Левую часть выражения написанного выше, можно обозначит с помощью функции от сопротивления технологической шунтировки и построить график зависимости, а точка пересечения графика с прямой проведённой из начала координат под углом 45 градусов, даёт нам значение искомого сопротивления:

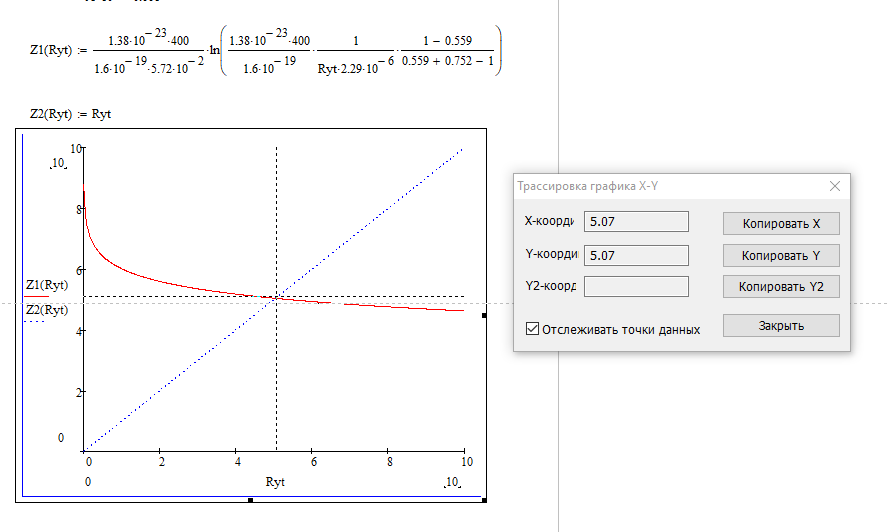
Рисунок 4 – График искомого сопротивления
Сопротивления технологической шунтировки перехода j₃ тиристора R_ут = 5.1 Ом*см².

Узнав сопротивление технологической шунтировки и задавшись величиной диаметра технологического шунта d_ш = 0.025 см, расстояние между центрами соседних шунтов можно рассчитать по формуле:
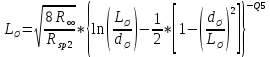(30)
Из формулы (30) выразим R_ут через L_ш:

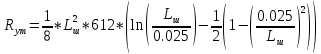
Расстояние между центрами соседних шунтов определим из таблицы ниже:
Таблица 4 – Расстояние между центрами соседних шунтов перехода j₃ тиристора L_ш.


Расстояния между центрами соседних шунтов перехода j3 тиристора L_ш = 0.21 см.

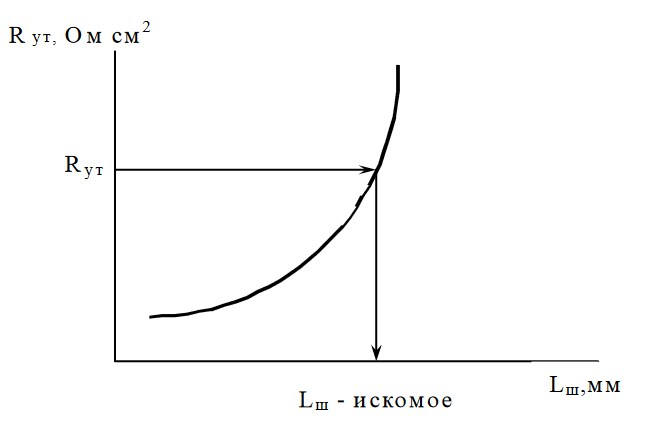
Рисунок 5 – Определения расстояния между центрами соседних шунтов

2. 
   Расчёт диаметра тиристорного элемента и выбор конструкции корпуса
   

Рассчитываем зависимость напряжения в открытом состоянии от плотности тока тиристора:
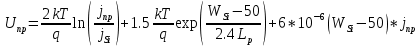, (32)
где 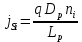при Т = 20

---

.
.
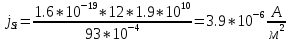Зависимость напряжения в открытом состоянии от плотности тока тиристора имеет вид:

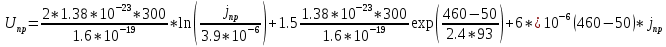
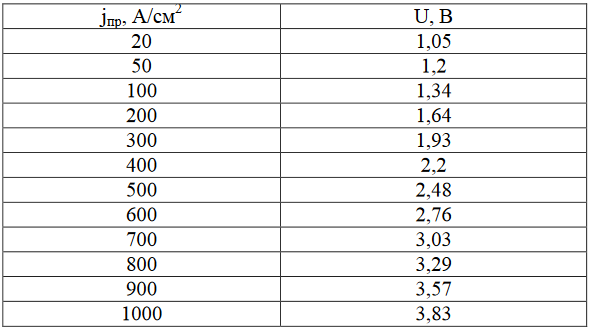
Результаты расчёта сведены в табл. 2.
Таблица 2 – Зависимость напряжения в открытом состоянии от плотности тока тиристора


Зависимость напряжения в открытом состоянии от плотности тока тиристора имеет вид, приведённый на рис. 6.

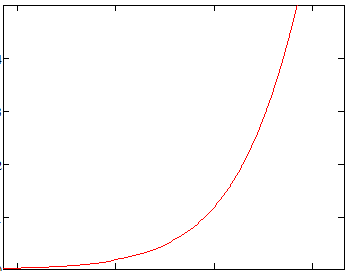
Рисунок 6 – Зависимость напряжения в открытом состоянии от плотности тока тиристора
Далее нам необходимо рассчитать радиальный размер фаски, которая используется для защиты структур силовых тиристоров от поверхностного пробоя. Для тиристоров, обычно, используют двухступенчатые фаски.

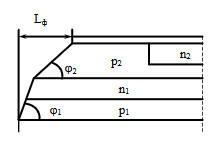
Рисунок 7 – Двухступенчатая фаска
Угол φ1- выбирается в пределах (30 – 45) , а угол φ2, определяющий стойкость к поверхностному пробою коллектор-ного перехода, в пределах (1,5 – 4). Радиальный размер фаски определяется по формуле ниже:
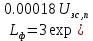) - 2 (мм). (33)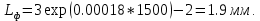

Далее нам необходимо определить коэффициент, учитывающий потери активной площади за счёт технологической шунтировки перехода j₃. Катодные шунты обычно имеют круглую форму и располагаются по площади эмиттера в виде регулярной системы с квадратным или треугольным расположением.

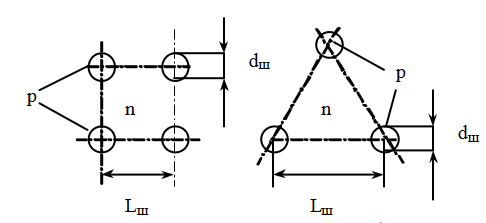
Рисунок 8 – Расположение шунтов катодного эммитера

Наличие эмиттерных шунтов приводит к потери общей площади эмиттера, а, следовательно, и нагрузочного тока. Коэффициент, учитывающий потери активной площади за счет технологической шунтировки перехода j3:

При расположении шунтов по вершинам квадратов:
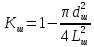, (34)
При расположении шунтов по вершинам треугольников:
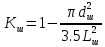, (35)
При треугольном распределении диаметр шунта больше, чем при квадратном, что позволяет лучше реализовать данную форму.

---

Выбираем расположении шунтов по вершинам треугольников:

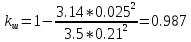
Задаёмся различными значениями диаметра выпрямительного элемента d_вэ и расcчитываем активную площадь структуры тиристора:
(36)
Вычисляем плотность тока через структуру при прямом токе, равном 2,5 I_ос.ср, и разных значениях d_вэ:
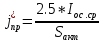(37)

Зная плотности тока, по графику зависимости напряжения в открытом состоянии от плотности тока тиристора определяем значение прямого напряжения и рассчитываем среднюю мощность прямых потерь Рос.ср. для разных значений dвэ, которое у нас 18 мм:
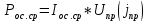(38)
Результаты расчёта приведены в таблице 3.

Далее рассчитываем графики зависимости мощности, рассеиваемой корпусом тиристора штыревой и таблеточной конструкции при заданных значениях максимально допустимой температуры структуры и корпуса, и строим их на графике.
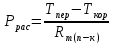(39)
Далее рассчитаем активную площадь структуры тиристора по формуле (36):

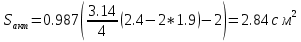
Исходя из всего выше написанного выбираем штыревой корпус.

2. 
   Расчёт основных параметров тиристоров
   

Импульсное напряжение в открытом состоянии определяем следующим образом. Зная d_вэ и активную площадь рассчитываем плотность прямого тока, соответствующую току I_ос.ср: j_ос.max= 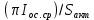. Далее по зависимости j_пр(U_пр) определяем U_ос.и=f(j_ос.max).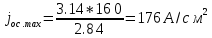



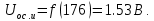
Повторяющийся импульсный обратный ток и повторяющийся импульсный ток в закрытом состоянии:
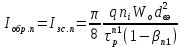(40)
Толщина слоя объёмного заряда W₀=W_on1 + W_op2, вычисляется по формулам (12), (15) – (17) при U_зс = U_зс.п.

---

Смотрите также файлы

• Задание Формирование досье, составление дерева целей.docx

• Человек, как основная тема философии Бердяева.docx

• Контрольная работа специальности 40. 02. 01 Право и организация социального обеспечения по дисциплине Трудовое право.docx

• Енот Место обитания.docx

• Тема Культурогенез в первобытную эпоху Задание 1.docx