Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Математика.docx
Добавлен: 03.12.2023
Просмотров: 139
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
AB:
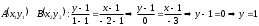 ВС:
ВС: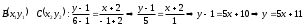
АС:
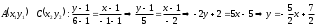
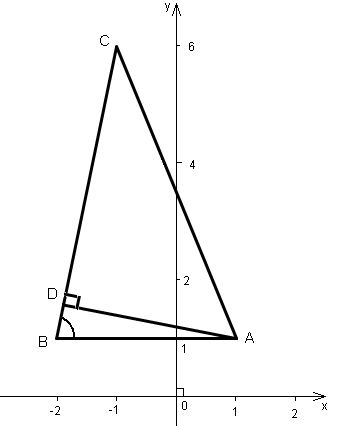
Для нахождения уравнения высоты AD находим угловой коэффициент прямой ВС:
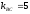 .
. Так как прямые AD и BC перпендикулярны, то воспользуемся условием перпендикулярности прямых:
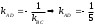 .
.Находим уравнение высоты AD , используя формулу уравнения прямой проходящей через т. М (x1;y1) в данном направлении:
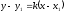
AD:
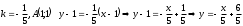 .
.
-
Для определения угла АВС треугольника используем формулу тангенса угла между двумя прямыми, угловые коэффициенты которых соответственно равны k1 и k2:
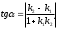 где α
где α  [0;
[0;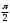 ]
]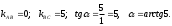
-
Площадь треугольника найдем, используя формулу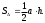
Основанием треугольника выберем отрезок ВС, а высотой соответственно отрезок AD. Тогда
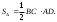
BC=
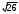
Расстояние AD можно найти как расстояние от точки A (x0;y0) до прямой
BC: Аx+By+C=0 по формуле:
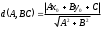
А (1;1), ВС: 5x-y+11=0
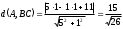
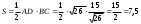 ед.2
ед.2ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
2 семестр
Выбор вариантов
| Начальные буквы фамилий студентов | Вариант |
| А, Б В, Г Д, Е, Ж З, И, К, Л, М Н, О, П Р, С Т, У, Ф, Х Ц, Ч, Ш, Щ Э, Ю, Я | 1 2 3 4 5 6 7 8 9 10 |
По каждому заданию в контрольных работах имеются методические указания, в которых подробно разобраны подобные задачи.
Тема 1. Элементы комбинаторики. События и их вероятности,
классический и геометрический способы подсчета вероятностей
Вариант 1. Среди 40 деталей 3 нестандартные. Наудачу взяты 2 детали. Найти вероятность того, что они нестандартные.
Вариант 2. В урне 3 белых и 7 чёрных шаров. Какова вероятность того, что вынутые наугад два шара окажутся белыми?
Вариант 3. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.
Вариант 4. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
Вариант 5. Товаровед получил 50 одинаковых изделий, среди них 5 бракованных. Наудачу для контроля взяты путём случайного выбора три изделия. Найти вероятность того, что среди них окажется ровно одно бракованное.
Вариант 6. Из партии, в которой 30 деталей без дефекта и 5 с дефектом, берут наугад три детали. Какова вероятность того, что среди них ровно две детали без дефекта?
Вариант 7. Среди 17 студентов группы, из которых 8 – девушки, разыгрывается 7 билетов в театр. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки и 3 юношей?
Вариант 8. На складе имеется 15 телевизоров, причем 10 из них изготовлены отечественным производителем. Найти вероятность того, что среди пяти взятых наудачу телевизоров окажутся три отечественных телевизора.
Вариант 9. Найти вероятность того, что точка брошенная в круг радиуса 1, окажется вне вписанного в этот круг квадрата.
Вариант 10. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного треугольника.
Тема 2.Операции над событиями.
Правила сложения и умножения вероятностей
Вариант 1. Заводом послана автомашина за различными материалами на 4 базы. Вероятность наличия нужного материала на первой базе равна 0,9; на второй – 0,95; на третьей – 0,8; на четвёртой – 0,6. Найти вероятность, того что только на одной базе не окажется нужного материала.
Вариант 2. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для – второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
Вариант 3. Производится три выстрела по одной и той же мишени. Вероятность попадания при первом выстреле равна 0,4; при втором – 0,5 и при третьем – 0,7. Найти вероятности следующих событий: А = {ровно одно попадание}; В = { хотя бы одно попадание}; С = { хотя бы два попадания}.
Вариант 4. В телеателье имеется три телевизора. Вероятности неисправности каждого из них соответственно равны 0,1; 0,2; 0,1. Какова вероятность того, что среди этих телевизоров исправными окажутся: 1) ровно два; 2) хотя бы один.
Вариант 5. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трёх проверенных изделий только два изделия высшего сорта.
Вариант 6. В сессию студент должен сдать 4 экзамена. Вероятность не выдержать первый – 0,1, для последующих экзаменов – 0,2; 0,15; 0,25 соответственно. Какова вероятность того, что студент сдаст хотя бы один экзамен?
Вариант 7. Устройство состоит из трёх элементов, работающих независимо. Вероятности безотказной работы первого, второго и третьего элементов соответственно равны 0,6; 0,7;08. Найти вероятность того, что безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента.
Вариант 8. Брошены три игральные кости. Найти вероятность того, что на каждой из выпавших граней появится пять очков.
Вариант 9. Первый магазин может выполнить план с вероятностью 0,9; второй – с вероятностью 0,8, а третий – с вероятностью 0,85. Найти вероятность того, что план выполнят не менее двух магазинов.
Вариант 10. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, а вторым стрелком – 0,6. Найти вероятность того, что цель будет поражена только одним стрелком.
Тема 3. Формула полной вероятности. Формулы Бейеса
Вариант 1. Сборщик получил 6 коробок деталей, изготовленных заводом №1, и 4 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,8, а завода №2 – 0,9. Сборщик случайно извлёк деталь из наудачу взятой коробки. Деталь оказалась стандартной.
Определить вероятность того, что она изготовлена на заводе №1.
Вариант 2. На сборку попадают детали с 3 автоматов. Известно, что первый автомат дает 3% брака, второй – 2% и третий – 4%. Найти вероятность того, что на сборку попадает бракованная деталь, если с первого автомата поступает 100, со второго – 200, с третьего – 250 деталей.
Вариант 3. Турист, заблудившийся в лесу, вышел на полянку, от которой в разные стороны ведут 5 дорог. Если турист пойдет по первой дороге, то вероятность его выхода из леса в течение часа составляет 0,6; если по второй – 0,3; если по третьей – 0,2; если по четвёртой – 0,1; если по пятой – 0,1. Какова вероятность того, что турист пошёл по первой дороге, если через час он вышел из леса?
Вариант 4. В сборочный цех завода поступают детали с трех автоматов. Вероятность поступления бракованной продукции с первого автомата составляет 0,03, для второго и третьего автоматов эти вероятности равны соответственно 0,01 и 0,02. Определить вероятность попадания на сборку небракованной детали, если с каждого автомата в цех поступило соответственно 500, 200 и 300 деталей.
Вариант 5. Известно, что в партии из 600 электрических лампочек 200 изготовлены на первом заводе, 250 на втором, 150 – на третьем. Вероятности того, что лампочка окажется стандартной при изготовлении на первом, втором, третьем заводах соответственно равны 0,97, 0,91 и 0,93. Какова вероятность того, что взятая наудачу лампочка окажется стандартной, изготовлена вторым заводом?
Вариант 6. При проверке качества зёрен пшеницы было установлено, что зёрна могут быть разбиты на 4 группы. К зёрнам первой группы принадлежит 96 %, второй – 2%, третьей и четвёртой – по 1% всех зёрен. Вероятности того, что зёрна дадут колос, содержащий не менее 50 зёрен, для семян указанных групп равны соответственно 0,5; 0,2; 0,18 и 0,2. Найти вероятность того, что из взятого наудачу зерна вырастет колос, содержащий не менее 50 зёрен.
Вариант 7. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0,9; для велосипедиста – 0,8; для бегуна – 0,75. Вызванный наудачу спортсмен норму выполнил. Найти вероятность того, что это бегун.
Вариант 8