Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Математика.docx
Добавлен: 03.12.2023
Просмотров: 141
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
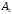 ={ студент ответил на третий вопрос },
={ студент ответил на третий вопрос },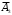 ={ студент не ответил на третий вопрос }.
={ студент не ответил на третий вопрос }.События
 и
и  – противоположные, поэтому
– противоположные, поэтому 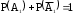 ,
, 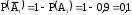 . Аналогично
. Аналогично 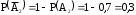 и
и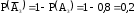 .
.а) Событие
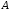 ={студент ответил только на один вопрос}.
={студент ответил только на один вопрос}.Появление события А означает, что наступило одно из трёх несовместных событий: либо


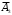 , либо
, либо 

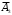 , либо
, либо 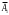
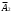
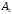 . По правилу сложения вероятностей
. По правилу сложения вероятностей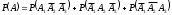 . События
. События  ,
,  ,
, 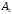 - независимые, следовательно, независимы и события
- независимые, следовательно, независимы и события  ,
,  ,
, 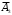 . По правилу умножения вероятностей для независимых событий
. По правилу умножения вероятностей для независимых событий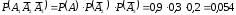 .
. Аналогично
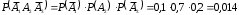
,
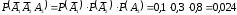 .
.Тогда
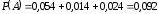 .
.б) Событие Б={студент ответил на все вопросы}. Наступление события Б означает, что одновременно появились независимые события
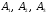 , т. е.
, т. е. 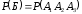 . По правилу умножения вероятностей для независимых событий
. По правилу умножения вероятностей для независимых событий ;
; 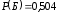 .
.в) Событие В ={ студент ответил хотя бы на один вопрос }. Это означает, что был дан ответ на любой один вопрос, или на любые два вопроса, или на все три вопроса. Событие
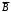 = {студент не ответил ни на один вопрос}. События B и
= {студент не ответил ни на один вопрос}. События B и 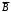 противоположны, поэтому
противоположны, поэтому 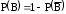 . Событие
. Событие 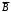 означает, что одновременно появились независимые события
означает, что одновременно появились независимые события  ,
, и
и  , т. е.
, т. е. 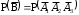 . По правилу умножения вероятностей для независимых событий
. По правилу умножения вероятностей для независимых событий 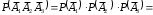
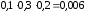 .
. Итак,
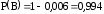 .
.г) Событие Г={студент ответил по крайней мере на два вопроса}. Это означает, что дан ответ на любые два вопроса или на все три вопроса. Появление события Г означает, что наступило одно из четырёх несовместных событий: либо
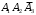 , либо
, либо 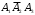 , либо
, либо 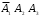 , либо
, либо 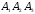 . По правилу сложения вероятностей несовместных событий
. По правилу сложения вероятностей несовместных событий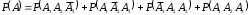 .
.События
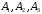
- независимые, следовательно, независимы события
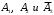 . По правилу умножения вероятностей независимых событий
. По правилу умножения вероятностей независимых событий 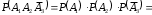
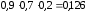 .
.Аналогично получаем
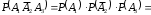
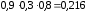 ,
,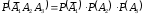
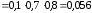 ,
,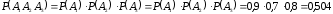 . Окончательно имеем
. Окончательно имеем 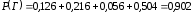 .
.д) Событие Д={ студент ответил на два вопроса }. Появление события Д означает, что наступило одно из трёх несовместных событий: либо
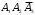 , либо
, либо  , либо
, либо 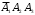 . Далее, используя решение задачи г), имеем
. Далее, используя решение задачи г), имеем 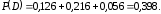
Тема 3. Формула полной вероятности. Формулы Бейеса
-
Формула полной вероятности
Пусть событие А может наступить лишь при появлении одного из множества попарно несовместных событий (гипотез) H1, H 2 , …, Hn . Тогда вероятность события А вычисляется по формуле полной вероятности
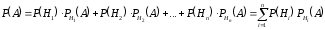 .
.События H1, H 2 , …, Hn называются гипотезами по отношению к событию А.
-
Формулы Бейеса
Если событие А уже произошло, то вероятности гипотез (априорные вероятности) могут быть переоценены (апостериорные вероятности) по формулам Бейеса
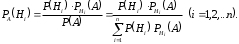
Пример 5. (Варианты 2, 4, 6, 8)
В ателье имеются 5 плейеров, выпущенных заводом B, 10 плейеров – заводом C, 15 плейеров – заводом D. Вероятность того, что плейеры, выпущенные заводами B, С, D, выдержат гарантийный срок службы, соответственно равны 0,8, 0,85 и 0,9. Найти вероятность того, что взятый наудачу плейер выдержит гарантийный срок службы.
Решение:
Событие А = {плейер выдержит гарантийный срок службы},
Гипотеза H1 = {плейер выпущен заводом В},
Гипотеза H2 = {плейер выпущен заводом С},
Гипотеза H3 = {плейер выпущен заводом D}.
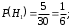
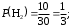

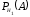 =0,8;
=0,8; 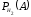 =0,85;
=0,85; 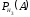 =0,9.
=0,9.По формуле полной вероятности
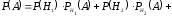
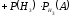
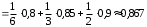 .
.Пример 6. (Варианты 1, 3, 5, 7, 9, 10)
Литьё в болванках поступает из двух заготовительных цехов: 70% из первого цеха, 30% из второго цеха. Литьё первого цеха имеет 10% брака, второго – 20% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность её изготовления первым цехом?
Решение:
Событие А ={болванка без дефекта}.
Гипотеза H1 – болванка изготовлена первым цехом,
Гипотеза H2 – болванка изготовлена вторым цехом,
Литьё первого цеха имеет 10% брака, следовательно, 90% болванок, изготовленных первым цехом, не имеют дефекта и
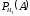 =0,9. Литьё второго цеха имеет 20% брака, следовательно, 80% болванок, изготовленных вторым цехом, не имеют дефекта и
=0,9. Литьё второго цеха имеет 20% брака, следовательно, 80% болванок, изготовленных вторым цехом, не имеют дефекта и 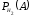 =0,8. Необходимо найти
=0,8. Необходимо найти 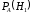 .
. По формуле Бейеса
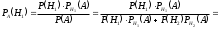
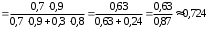 .
.Тема 4. Повторение независимых испытаний.
-
Формула Бернулли
Вероятность того, что в серии из п независимых испытаниях, в каждом из которых вероятность появления события A равна p (0р1), это событие наступит ровно k раз (безразлично в какой последовательности), равна
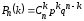 ,
,где
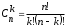 – число сочетаний из n по k (см. выше), q=1-p– вероятность противоположного события
– число сочетаний из n по k (см. выше), q=1-p– вероятность противоположного события 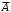 .
.В различных задачах нас могут интересовать следующие вероятности:
– вероятность того, что в п испытаниях событие A наступит менее m раз
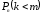 =
=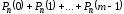 ;
;– вероятность того, что в п испытаниях событие A наступит более m раз
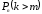 =
=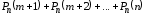 ;
;– вероятность того, что в п испытаниях событие A наступит не менее m раз
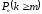 =
=